峰值折射率对正弦型函数光子晶体带隙的影响
2014-10-25熊翠秀邓杨保邓曙光
熊翠秀,邓杨保,邓曙光
(湖南城市学院通信与电子工程学院,湖南益阳413000)
1 引言
光子晶体是折射率或介电常数按周期性变化的人工微结构材料,其概念最早于1987年分别由 S.John 和 E.Yablonovitch 提出[1-2],光子禁带和光子局域是光子晶体的基本特性。早些年的研究主要集中在常规光子晶体上。为了适合各个不同应用场合的需求,近年陆陆续续提出了不同结构的非常规光子晶体[3-16],折射率与空间坐标有关的函数型光子晶体[12-16]就是其中的一类非常规光子晶体。文献[12]~[16]根据费马原理,推导了函数型光子晶体中的传输矩阵和色散方程,研究了一维正弦型函数光子晶体的透射谱和色散关系。其中文献[12]和[14]在折射率函数的系数一定情况下,详细研究了入射角和介质层的厚度对一维正弦型函数光子晶体带隙结构的影响,文献[15]研究了周期数和入射角对一维正弦型函数光子晶体带隙结构的影响,这些文献报道,通过选择不同的折射率空间分布函数,可以得到比常规光子晶体更宽或更窄的禁带。但都没有涉及正弦型函数的折射率系数对带隙结构的影响,虽然文献[16]给出了不同系数下的透射谱和色散关系,但系数变化的同时入射角也在变化,故没有给出各个系数对带隙结构的影响。为了探讨正弦函数的折射率系数对一维光子晶体带隙结构的影响,笔者先把正弦型函数折射率介质层离散化[17],用平均折射率等效为每一小层的折射率,再用传输矩阵法[18]计算光子晶体的透射率和色散关系,分析各个系数对透射谱带隙结构的影响。结果表明,各个系数对带隙结构的影响有所不同,且各自呈现一定的规律。这为光子晶体的设计提供一定的理论依据。
2 理论模型和计算方法
2.1 理论模型
折射率与空间坐标z按正弦规律变化的高折射率介质A和低折射率介质B交替排列,组成(AB)N形一维光子晶体,N表示周期数。令光波沿着z方向传播,介质A和B的折射率分别由式(1)和式(2)式表示:
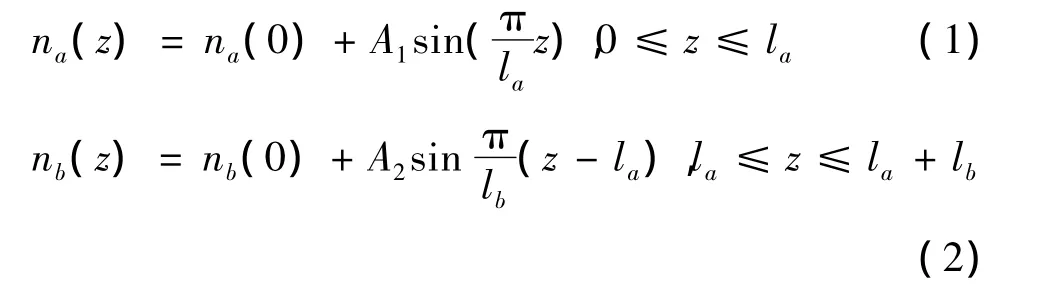
式中,la和lb分别是A和B介质的几何厚度;而na(0)和nb(0)分别是A和B介质起始端的折射率。
2.2 计算方法
对于常规一维光子晶体,可以直接采用传输矩阵法[18]计算透射率;对于一维函数光子晶体,由于折射率随空间坐标z变化,不能直接采用传输矩阵法。当把折射率按空间坐标z变化的介质层离散化,即把每半个周期分成J小层,每小层的几何厚度为(或),当J趋于无穷大时,每小层的折射率变化很小,每一小层都可以近似为常规折射率介质,故进行离散化后,每小层的光学传输特性可以用传输矩阵表示[17]。文献[17]在离散化介质层时,把每小层起始端的折射率作为该小层的折射率,而笔者在计算过程中用每小层的平均折射率等效为该小层的折射率。
3 结果与讨论
参数选取参照文献[13],即取la=114.985 nm和lb=250.972nm,na(0)=3.37 和nb(0)=1.544,N=16。在Matlab7.0环境下编程计算。上述参数对应的常规一维光子晶体的带隙结构如图1所示,其中图1(a)和图1(b)分别为透射谱和色散关系。由图知,主禁带在1246~2047 nm之间。

图1 常规一维光子晶体的带隙结构
3.1 高折射率介质层为正弦型函数介质
考虑高折射率介质A的折射率随空间坐标z按正弦函数规律变化,介质B为常规介质,即A2=0。每个A层离散化为J=20层。令垂直入射,则TE和TM波的透射谱一样。图2给出了介质A的折射率系数分别取 A1=0.1,0.2,0.3,0.5,0.6,0.9,1.0,1.2 时的带隙结构,其中图 2(a)和图2(b)分别对应于透射谱和色散关系。由图2知,随着A1的增大,主禁带上下带边都向长波方向移动,且下带边移动的速度比上带边快,故主禁带发生红移,且主禁带宽度增宽。

图2 高折射率介质的折射率按正弦规律变化时一维光子晶体的带隙结构
3.2 低折射率介质层为正弦型函数折射率介质
考虑低折射率介质B的折射率随空间坐标z 按正弦函数规律变化,介质A为常规介质,即A1=0。每个B层离散化为J=20层,令垂直入射。分别取A2=0.1,0.2,0.3,0.5,0.6,0.9,1.0,1.2,图 3 给出了相应的带隙结构,其中图3(a)和图3(b)分别对应于透射谱和色散关系。由图3知,随着系数A2的增大,主禁带的上下带边都向长波方向移动,但上带边移动的速度比下带边移动的速度快,从而导致主禁带波长中心发生红移,且带宽变窄;除此之外,由图3还可知,随着A2的增大,光子禁带数目增多,但每个禁带随A2的变化规律不一样,图中除主禁带外,向短波方向的第一个、第二个禁带带宽随A2的变化规律正好相反,第一个随A2的增大而增宽,而第二个则相反。

图3 低折射率介质的折射率按正弦规律变化时一维光子晶体的带隙结构
3.3 高低折射率介质均为正弦型函数折射率介质
考虑介质A和B的折射率都随空间坐标z按正弦函数规律变化。每个介质层都离散化为2 0层,令垂直入射。图4给出了系数A1和A2取一系列不同值对应的透射谱。图4(a)从上到下,(A1,A2)的值分别为(0.2,0.1)、(0.4,0.2)、(0.6,0.3)、(0.8,0.4)、(1,0.5)、(1.2,0.6)、(1.4,0.7)和(1.6,0.8),满足 A1>A2;图4(b)从上到下,(A1,A2)的值分别为(0.1,0.2)、(0.2,0.4)、(0.3,0.6)、(0.4,0.8)、(0.5,1)、(0.6,1.2)、(0.7,1.4)和(0.8,1.6),满足 A1<A2。由图4知,当 A1和 A2都增大时,带隙红移,且禁带个数增多。由图4(a)知,当A1>A2时,主禁带带宽比相同结构参数下的常规光子晶体的主禁带宽,且A1与A2的差值越大,主禁带越宽。除主禁带外,向短波方向有一系列次禁带,随着A1与A2差值的增大每个次禁带都略微增宽,但只有靠近主禁带的次禁带增宽现象明显;由图4(b)知,当A1<A2时,主禁带带宽比相同结构参数下的常规光子晶体窄,且A1与A2的差值越大主禁带越窄,除主禁带以外短波方向也有一系列的次禁带,这些次禁带表现出一定的规律性,具体为:除主禁带外,向短波方向数的第奇数个次禁带随A1与A2差值的增大而变宽,而第偶数次禁带则随A1与A2差值的增大而变窄,其中靠近主禁带的次禁带变化最明显。
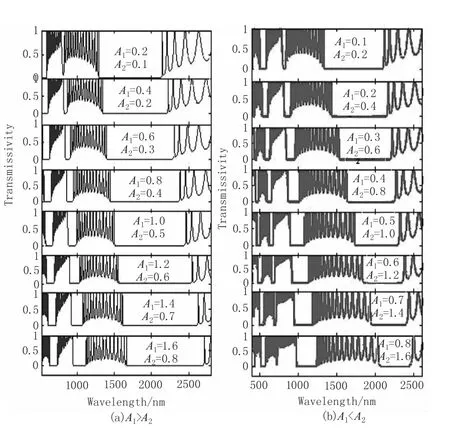
图4 高低折射率介质的折射率均按正弦规律变化时的透射谱
4 结 论
首先对折射率随空间坐标按正弦规律变化的介质层离散化,再采用传输矩阵法,计算了正弦型函数一维光子晶体的透射率,着重分析了高低折射率介质层的峰值折射率变化对透射谱主禁带的影响。研究表明,当正弦函数的系数发生变化,即介质的峰值折射率发生变化,从而使平均折射率发生变化时,与常规一维光子晶体相比,无论是高折射率介质还是低折射率介质的峰值折射率增大,或是二者的峰值折射率都增大,其透射谱的禁带都发生红移;如果高低折射率介质的平均折射率之差增大,则主禁带的宽度增宽,当高低折射率介质的平均折射率之差减小,则主禁带宽度变窄;次禁带也表现出一定的规律,但次禁带的规律与主禁带的变化规律不尽相同。这些结论对光子晶体的设计具有一定的指导意义。
[1] Yablonovitch E.Inhibited spontaneous emission in solid -state physics and electronics[J].Physical review letters,1987,58(20):2059 -2061.
[2] John S.Strong localities of photons in certain disordered dielectric super lattices[J].Phys Rev Lett,1987,58(23):2486-2489.
[3] WU J J.Effect of meterial dispersion on bandgap of one -dimensional graded photonic crystals[J].Journal of Synthetic Crystals,2011,40(2):474 -479.(in Chinese)武继江.材料色散对渐变结构一维光子晶体带隙的影响[J].人工晶体学报,2011,40(2):474 -479.
[4] XI F.Reronant modes in one - dimensional photonic crystal hetore - structures with metammterials[J].Laser &Infrared,2013,43(6):663 -667.(in Chinese)席锋.复合周期特异介质光子晶体异质结的谐振模[J].激光与红外,2013,43(6):663 -667.
[5] Kocaman S,Aras M S,Hsieh P,et al.Zero phase delay in negative-refractive-index photonic crystal superlattices[J].Nature Photonics,2011,5(8):499 -505.
[6] Rahimi H,Namdar A,Roshan Entezar S,et al.Photonic transmission spectra in one-dimensional fibonacci multilayer structures containing single-negative metamaterials[J].Progress in Electromagnetics Research,2010,102:15-30.
[7] Zyryanov V Y,Myslivets S A,Gunyakov V A,et al.Magnetic-field tunable defect modes in a photonic-crystal/Liquid - crystal cell[J].Optics express,2010,18(2):1283-1288.
[8] Wu C Y,Zou Y H,Timofeev I,et al.Tunable bi- functional photonic device based on one-dimensional photonic crystal infiltrated with a bistable liquid-crystal layer[J].Optics Express,2011,19(8):7349 -7355.
[9] Arkhipkin V G,Gunyakov V A,Myslivets S A,et al.Electro-and magneto-optical switching of defect modes in one - dimensional photonic crystals[J].Journal of Experimental and Theoretical Physics,2011,112(4):577-587.
[10] Thapa K B,Srivastava S,Tiwari S.Enlarged photonic band gap in heterostructure of metallic photonic and superconducting photonic crystals[J].Journal of superconductivity and novel magnetism,2010,23(4):517 -525.
[11] Wu J J,Gao J X.Extraordinary optical properties of fibonacci quasi-peri-odic 1D superconducting photonic crystals in near- zero - permittivity operation range[J].Optoelectronics Letters,2013,9(4):0289 -0292.
[12] WANG G H,WANG Q C,WU X Y,et al.Research on one- dimensional functional photonic crystals[J].Acta Physica Sinica,2012,61(13):134208.(in Chinese)王光怀,王清才,吴向尧,等.一维函数光子晶体的研究[J].物理学报,2012,61(13):134208.
[13] BA N,WU X Y,WANG J,et al.Light transmission properties of one - dimensional function photonic crystals[J].Chinese Journal of Lasers,2012,39(6):0606001.(in Chinese)巴诺,吴向尧,王婧,等.一维函数型光子晶体的光学传输特性[J].中国激光,2012,39(6):0606001.
[14] BA N,WANG Q C,LIU X J,et al.Investigation on one -dimensional sin - function photonic crystals[J].Jilin Normal University Journal,2012,33(1):34 - 37.(in Chinese)巴诺,王清才,刘晓静,等.一维正弦型函数光子晶体带隙结构研究[J].吉林师范大学学报,2012,33(1):34-37.
[15] WANG Q C,WANG Y,WANG G H.One - dimensional function photonic crystals[J].Journal of Jishou University,2012,33(1):36 -40.(in Chinese)王清才,王岩,王光怀.一维函数光子晶体的禁带特性理论[J].吉首大学学报,2012,33(1):36 -40.
[16] LIU X J,ZHANG S Q,WANG J,et al.One - dimensional new function photon crystals[J].Journal of Jilin University,2012,50(5):1020 -1024.(in Chinese)刘晓静,张斯淇,王婧,等.一维新型函数的光子晶体[J].吉林大学学报,2012,50(5):1020 -1024.
[17] LIU Q N.Polarization properties of the electromagnetic wave in photonic crystal with sinusoidal refractive index[J].Chinese Journal of Quantum Electronics,2008,25(2):198 -202.(in Chinese)刘启能.折射率正弦离散变化声子晶体中电磁波的偏振特性[J].量子电子学报,2008,25(2):198 -202.
[18] Born M,Wolf E.Principles of optics[M].Yang J S,et al transl.7th ed.Beijing:Publishing House of Electronics Industry,2009:59 -61.(in Chinese)马科斯·玻恩,埃米尔·沃尔夫.光学原理[M].杨葭荪,等译.7版.北京:电子工业出版社,2009:59-61.
