对当前初中生数学思维能力现状的研究和思考
2014-10-22周洪亚
周洪亚
摘 要: 思維能力是学习对象学习能力水平的重要内涵,是学习对象智力水平的重要特征。本文通过对学习对象思维能力水平的研究和分析,对当前初中生数学思维能力水平发展现状进行了研究分析,并就如何做好思维能力培养工作进行论述。
关键词: 初中数学教学 数学思维能力 培养途径
一、初中生数学思维能力现状
思维能力是学习对象学习能力水平的重要内涵,是学习对象智力水平的重要特征。新课程标准强调指出,要将学习能力培养作为有效教学的第一要务。但由于应试教育和升学压力的影响和制约,以分数论“英雄”的传统教学活动重视学生解题活动教学,忽视思维能力水平培养,初中生思维能力水平的现状主要呈现以下特征。
一是主动思维意识淡薄。部分初中数学教师在应试教育“大棒”的驱使下,忽视学习对象思维能动情感的激发,采用单一、单向、传统的教学模式。一方面不能将自身具有的引导、指导特性充分发挥,另一方面不能充分利用数学学科隐含的丰富情感教学资源,营造轻松、融洽的教学氛围,引发学生主动思考分析的潜能和欲望,导致初中生不愿开展思考、分析和归纳等思维活动。
二是缺少思维实践活动时机。部分初中数学教师过分强调教师的主导作用,将课堂教学中的师生双边活动变革为教师讲解为主的单向活动,学生主体能动特性受到压制,只能被动接受教师“直接”灌输的知识经验,缺少自主探究实践的活动时机,面对实际问题“手足无措”。
三是解析方法不够灵活。部分初中生在感知、分析、解答数学问题案例的过程中,由于未能掌握思考、分析、解答问题的基本方法和规律策略,围绕问题案例解答要求,不能正确对问题条件及解题要求之间的关系进行深入探析,对解答问题的思路不能进行科学、全面规划。特别对较复杂的数学问题,不能根据已掌握的解题方法进行“变通”和创新,不能运用灵活的解题方法解答问题案例。如在全等三角形的判定案例教学中,判定三角形全等的方法有好几种,但学生面对实际问题时,对如何判断三角形全等的方法产生疑惑,不能结合问题要求,采用多种多样的判断方法证明其全等,根本原因在于学生对判断的方法运用不够灵活。
四是综合归纳技能薄弱。数学学科知识点关系紧密、关联深刻,是一个紧密联系的有机整体。囊括多个知识点的综合性问题,在问题案例解答中经常出现,但初中生在解析该类型问题案例时,运用多种解题策略或解题思想方法等技能素养还较低,综合归纳、逻辑推理等方面的思考判断能力需进一步提高,综合归纳的思维技能较薄弱。
二、培养初中生数学思维能力的途径
针对初中生数学思维能力的现状及问题,我认为应从以下方面着手进行有效解决。
一是利用丰富的情感资源,挖掘主动思维潜能。数学是思维的艺术,其发展进程及自身内容有着显著而鲜明的生动特性、现实特点、应用意义和趣味特征。数学学科的丰富情感资源为消除初中生思维活动的“消极”思想,坚定主动思维信念,提供了有利条件,奠定了坚实基础,将学生引入到主动思考、分析、探析问题的活动中。生活性是数学学科的最基本特性,任何社会、生活领域总能找寻到数学知识的“踪影”。同时,初中生对贴近现实生活的案例充满“亲近感”,成为驱动和激励学生主动思维的有效抓手。如在“正比例函数”案例教学中,教师为吸引学生注意力,调动其思维积极性,为其创设了“电信公司设置不同方案销售通讯费用”、“工人师傅向游泳池注水,注水时间和水位高度之间的关系”等现实生活情境,引发了学生的情感“共鸣”,带着积极情感主动思考分析问题案例。
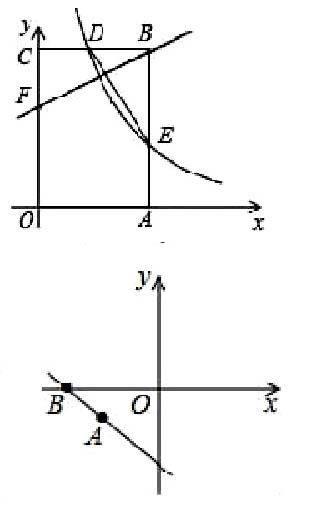
二是搭建实践探析载体,提供思考分析时机。学习能力的培养离不开实践探究的活动进程。初中生思维能力水平不高的一个重要方面,就是缺少直接实践、探析的活动过程。这就要求初中数学教师腾出一定的教学时间搭建具有实践探析意义的活动载体,提供学生进行思考、分析和探究的活动时机,引导学生将所学知识内容转化为思考探究的方法经验,指导学生深刻地思考分析解答问题案例,获得解决问题的方法和策略,形成思考分析解答问题的经验技能。如在“如图,矩形BC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3)。双曲线y=k/x(x>0)的图像经过BC的中点D,且与AB交于点E,连接DE。求k的值及点E的坐标”的案例教学中,教师采用“探究性教学策略”,学生探析问题条件内容后,根据解题要求,展示其思考分析过程:“根据B的坐标,以及四边形ABCO为矩形,确定出BC中点D坐标,代入反比例解析式求出k的值;根据E在反比例图像上,且B与E横坐标相同,确定出E坐标即可。”教师对学生的解题思路进行实时指导,在其解答活动后,引导、指导其归纳总结解题策略。此案例教学过程中,学生获得思考、分析、解析问题解答思路、解题策略的实践探究活动,掌握思考分析问题的一般方法和策略,思维能力得到有效锻炼和提升。
三是重视解题方法传授,提高思维能力。初中数学学科案例解答的思想策略有函数与方程的思想、数形结合的思想、分类讨论的思想、转化与化归的思想等,基本方法有换元法、配方法、构造法、待定系数法、公式法及反证法等。教师在思维能力培养中要重视解题方法的传授,一方面设置具有典型特征的问题案例,另一方面结合案例进行针对性讲解,向学生传授解题方法的内涵、要义及注意点,使学生能够真正认识和掌握解题方法的精髓,正确、高效地应用于问题解答活动。如在“如图,直线y=kx+b经过A(-2,-1)和B(-3,0)两点,则不等式组1/2x 四是注重综合问题教学,提高综合思维素养。初中数学教师应抓住数学知识点之间的深刻联系,设置具有综合特性的数学问题,引导学生结合多种解题方法进行分析、解答问题活动,指导学生根据题意选择和应用多种多样的解题方法或策略,正确、完备地解决综合性数学问题,提高初中生综合应用的思维能力。
