含裂纹碳纳米管轴压性能的分子动力学模拟*

韩强 王彩红 姚小虎

(华南理工大学 土木与交通学院，广东 广州510640)

碳纳米管(CNTS)［1］具有优异的力学、电学、热学等性质，在实验和理论研究中已广泛用于复合材料，能够极大改善材料的性能. 碳纳米管优异的力学性质与其结构特性密切相关，然而在生产过程中不可避免地会出现各种缺陷，特别是Stone-Wales(SW)及空位缺陷［2］，这些缺陷的存在会削弱碳纳米管的拉压等性能.碳纳米管在轴压荷载作用下发生屈曲行为［3］，辛浩等［4］采用Morse 势函数，研究了含单双原子及SW 缺陷碳纳米管的轴压屈曲性能，认为各类缺陷均会显著降低纳米管的屈曲性能.Hirai 等［5］研究了沿轴向分布的空位缺陷对碳纳米管压缩性能的影响，发现在缺陷处存在应力集中现象，轴压屈曲荷载明显减小. Huq 等［6］采用分子力学模拟，研究了SW 缺陷对单层碳纳米管轴压行为的影响.Zhang 等［7］运用分子动力学模拟，研究了SW 及空位缺陷对单层碳纳米管轴压性能的影响，结果表明，缺陷大大削弱了碳纳米管的临界屈曲荷载.Ang 等［8］采用Compass 势，研究了含1 －3个空位缺陷的单层碳纳米管的轴压屈曲行为. Kulathunga 等［9］采用Compass 势函数，研究了含对称与非对称空位缺陷单层碳纳米管的轴压行为. Chowdhury等［10］采用Brenner 势函数，研究了完善及含缺陷碳纳米管的拉压扭转等力学性能，认为空位缺陷对碳纳米管的影响高于SW 缺陷.Vijayaraghavan 等［11］采用Airebo 势函数，研究了含缺陷单层碳纳米管轴压行为.Kinoshita 等［12］采用Airebo 势函数，分析了含SW 缺陷碳纳米管的轴压性能. Eftekhari 等［13］采用Tersoff 势函数，分别研究了含空位及SW 缺陷的单层与双层碳纳米管的轴压性能，研究表明，SW 缺陷对碳纳米管屈曲性能的影响较空位缺陷显著. 可见，已有的工作多是对含单双空位及SW 缺陷的研究，关于含裂纹碳纳米管轴压性能的研究工作很少.

文中运用分子动力学方法，对含裂纹扶手椅型碳纳米管的轴压性能进行了模拟分析，重点考虑了裂纹尺寸及管长变化对碳纳米管轴压屈曲性能的影响，详细分析了含不同裂纹尺寸碳纳米管及不同长度纳米管的轴压变形特性.

1 分子动力学模拟

1.1 碳纳米管的物理模型

文中以扶手椅型(7，7)及(10，10)碳纳米管为研究对象，模拟过程中，碳纳米管的长度变化范围为6 ～30 nm. 在碳纳米管中心附近区域，沿着与轴向成30°及90°方向去掉一定数目的碳原子，构建出与轴向成不同倾角θ 的裂纹，设定初始裂纹尺寸为CL，在模拟过程中分别取为0.000、0.710、0.994及1.562 nm，其中裂纹尺寸为0.000 nm 表示完善的碳纳米管.计算模型结构如图1 所示.

图1 长度为6 nm 的(7，7)碳纳米管的结构Fig.1 Structures of (7，7)carbon nanotube with a length of 6nm

1.2 分子动力学模拟方法

分子动力学计算的一个关键问题是原子势函数的选取，文中选用Airebo 势函数［14］，这是一种改进的Rebo 势函数，能够较为真实地反映碳元素所构成的固态材料的物理性质.

模拟过程中，控制X、Y、Z 方向为自由边界条件，沿着碳纳米管轴向为加载方向，固定一端碳原子，对另一端碳原子施加恒速压缩位移载荷. 采用Nose-Hoover 热浴法［15-16］进行温度调节，使系统保持在特定的温度下，采用Velocity-Verlet 算法［17］进行分子动力学计算.加载之前先对碳纳米管进行充分无约束弛豫，使整个系统处于能量最低的平衡状态.对弛豫过的碳纳米管施加轴压位移载荷，每步应变量为0.000 5，然后进行充分的弛豫，重复此加载、弛豫过程，直至碳纳米管压缩破坏.

2 模拟结果分析

2.1 裂纹尺寸对碳纳米管轴压性能的影响

为研究裂纹尺寸变化对碳纳米管轴压屈曲性能及变形特性的影响，选取长度为6 nm、初始裂纹尺寸分别为0.0、0.71、0.994 及1.562 nm 的(7，7)与(10，10)碳纳米管进行模拟分析，模拟过程中控制温度为0.01 K，以避免热激活的复杂影响，时间步长取1 fs.

2.1.1 垂直于轴线方向的裂纹

采用分子动力学方法，模拟含有垂直于轴向裂纹的(7，7)、(10，10)扶手椅型碳纳米管在轴压载荷作用下的屈曲及后屈曲变形行为.为了进行对比分析，首先模拟了完善(7，7)管的轴压屈曲变形性能，其纳米管直径约0.95 nm.

文中与辛浩［4］及Yakobson 等［3］所选取的势函数、分子动力学计算方法及模型尺寸不完全相同，将他们的结果与文中的模拟结果进行对比分析可知(如表1 所示)，文中得到的(7，7)管轴压临界屈曲应变与他们的结果很接近，可见Airebo 势函数可以较好地描述碳纳米管中的C—C 键作用.

表1 完善(7，7)碳纳米管在轴压变形过程中关键点的应变值Table 1 Critical strains of perfect (7，7)CNTs during axial compression

由图2 可知，对于完善碳纳米管，随着压缩进行，其轴向应力呈非线性变化.图2 中a、b、c、d 四点与图3(a)、3(b)、3(c)、3(d)一一对应，当轴压应变为0.1347(图中d 点)时，碳纳米管彻底压缩破坏.

图2 完善(7，7)碳纳米管的轴压应力－应变曲线Fig.2 Stress-strain curve of perfect (7，7)carbon nanotube under axial compression

图3 完善(7，7)碳纳米管的轴压变形Fig.3 Configurations of perfect (7，7)carbon nanotube under axial compression

图4 θ=90°、裂纹尺寸为0.71nm 的(7，7)管的轴压应力－应变曲线Fig.4 Stress-strain curve of (7，7)tube with the crack length of 0.71 nm under axial compression when θ=90°

图5 θ=90°、裂纹尺寸为0.71 nm 的(7，7)管的轴压变形Fig.5 Configurations of (7，7)tube with the crack length of 0.71 nm under axial compression when θ=90°

图4 和5 给出了裂纹尺寸为0.71 nm 的(7，7)碳纳米管在轴压过程中的应力－应变曲线及变形形态. 由图5可知，在轴压过程中，含裂纹(7，7)管的变形形态与完善(7，7)管有明显区别，对于完善碳纳米管(如图3 所示)，随着压缩进行，管壁某处发生凹陷后，凹陷会沿着轴向进行传播，管壁发生凹陷的地方可能会回弹.然而对于裂纹尺寸为0.71 nm的纳米管，在整个轴压过程中，裂纹处的凹陷没有发生回弹，这是由于裂纹处缺少相应的支撑作用.

裂纹附近区域受力不均匀，在压缩至a 点时，裂纹区域出现局部凹陷变形.与完善(7，7)管相比，裂纹尺寸为0. 71 nm 时，其临界屈曲强度下降了40.4%，当压缩至b 点时，与裂纹部位相对应的另一侧管壁出现凹陷. 对比完善管及含裂纹(7，7)管的应力－应变曲线可知，在b、c、d 处两种管内的应力差别较小，可见裂纹尺寸为0.71 nm 时，纳米管屈曲后轴向承载力的变化不大.碳纳米管最终在裂纹处弯折破坏.

图6、7 给出了裂纹尺寸为0.994 nm 的(7，7)管的轴压性能. 由图7 可知，裂纹尺寸为0. 994 与0.71 nm的(7，7)管的轴压过程相似，在裂纹附近处均出现凹陷并最终在裂纹处压缩破坏，在整个轴压过程中，裂纹处的凹陷没有发生回弹.由图6可知，碳纳米管在轴压过程中荷载变化较为频繁，在未达到临界屈曲强度之前出现a、b 两个波动点，两点对应的变形结构表明含裂纹一侧的管壁出现凹陷.压缩至c 点时，管壁另一侧也出现凹陷，此时纳米管达到轴压屈曲强度. 与完善管相比，其屈曲强度降低了45.4%.

图6 θ =90°、裂纹尺寸为0. 994 nm 的(7，7)管的轴压应力－应变曲线Fig.6 Stress-strain curve of (7，7)tube with the crack length of 0.994 nm under axial compression when θ=90°

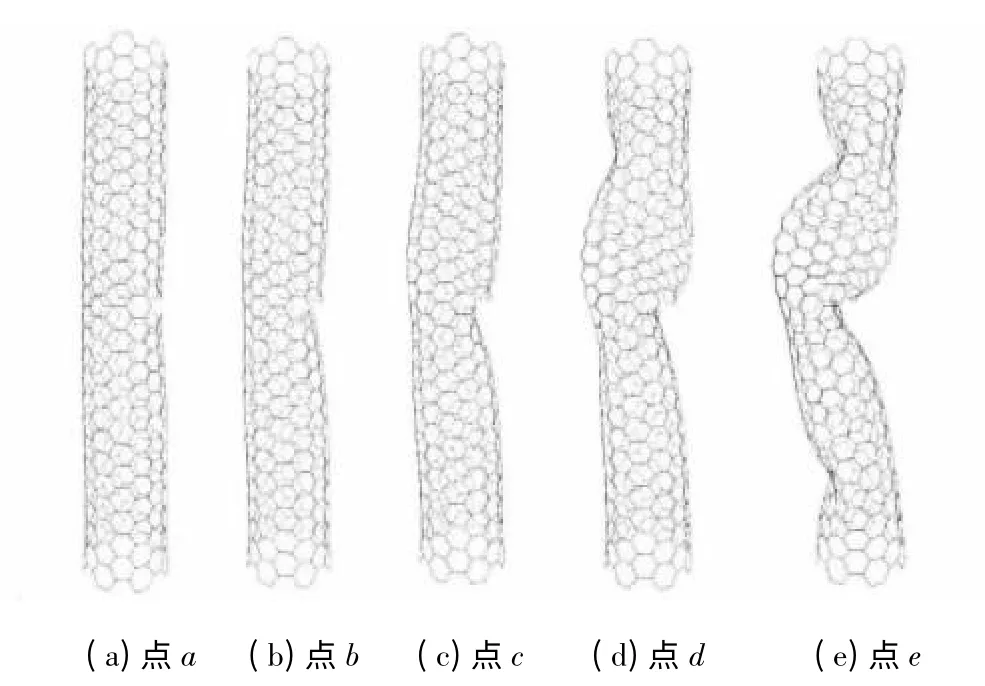
图7 θ=90°、裂纹尺寸为0.994 nm 的(7，7)管的轴压变形Fig.7 Configurations of (7，7)tube with the crack length of 0.994 nm under axial compression when θ=90°

对比裂纹尺寸为0.994 与0.71 nm 的(7，7)管的变形可知，随着裂纹尺寸增加，裂纹处的凹陷略有差别，对于裂纹尺寸较大的纳米管，其凹陷处裂纹上下边缘呈现明显的错位，这是由于裂纹处缺少了沿轴向的支撑作用，裂纹尺寸增大时，这种缺失越明显.

图8 给出了(7，7)、(10，10)管的临界屈曲强度随裂纹尺寸的变化，随着裂纹尺寸增加，碳纳米管的屈曲强度均减小. 在裂纹尺寸由0 增加到1.562 nm的过程中，(7，7)与(10，10)管的轴向临界屈曲强度分别降低了57.05%及49.98%.

图8 θ=90°时临界屈曲强度随裂纹尺寸的变化Fig.8 Critical buckling strength vs.crack length when θ=90°

2.1.2 与轴线方向成30°角的裂纹

由上节可知，碳纳米管中部区域垂直于轴线的裂纹大大减弱了其轴向承载力，为了进行更加全面的分析，本节模拟分析了裂纹倾角为30°、管长为6 nm，含不同裂纹尺寸的(7，7)、(10，10)扶手椅型碳纳米管的轴压屈曲性能.

图9、10 给出了裂纹倾角为30°、尺寸为0.71 nm的(7，7)碳纳米管的轴压性能. 裂纹附近区域的管壁受力不均匀，碳纳米管压缩至a 点时，在裂纹附近的管壁首先发生凹陷变形，与完善管相比，其临界屈曲强度降低了40.6%. 随着荷载增加，管壁另一侧也出现凹陷(对应b 点形态图)，其后的变形及对应的轴向应力及势能变化与裂纹倾角为90°、尺寸为0.71nm 的(7，7)纳米管相似，轴压过程中相应的轴向应力小于裂纹倾角为90°的纳米管.

裂纹倾角为90°的(7，7)纳米管的凹陷出现在裂纹处，整个裂纹区域内凹，而裂纹倾角为30°、尺寸为0.71 nm 的(7，7)纳米管最开始出现的凹陷是在裂纹附近区域，而不是裂纹区域内凹，在裂纹边缘处出现扭曲现象. 对比二者的结构可知，当裂纹与轴向成30°角时，在轴向压缩作用下，裂纹的上、下两边缘处有斜向剪切作用，这个剪切作用引发裂纹区域的扭曲，可见裂纹结构差异会导致碳纳米管变形形态及性能的不同.

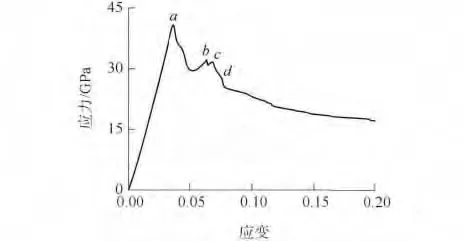
图9 θ=30°时裂纹尺寸为0. 71 nm 的(7，7)管的轴压应力－应变曲线Fig.9 Stress-strain curve of (7，7)tube with the crack length of 0.71 nm under axial compression when θ=30°

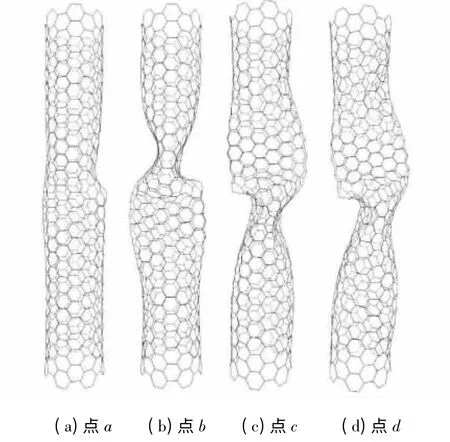
图10 θ=30°、裂纹尺寸为0.71nm 的(7，7)管的轴压变形Fig.10 Configurations of (7，7)tube with the crack length of 0.71 nm under axial compression when θ=30°

裂纹倾角为30°、尺寸为0.994 nm 的(7，7)碳纳米管的轴压性能如图11、12 所示.压缩至a 点时，纳米管达到其临界屈曲强度，与完善管相比，其值降低了51%. 由图可知，起初其变形形态及应力变化趋势与裂纹尺寸为0.71nm 的(7，7)管相似，在裂纹附近区域出现内凹，裂纹上下边缘出现扭曲现象.然而随着载荷增加，可以明显看到裂纹处出现剧烈的错位及撕扯，其纵轴线发生明显的弯折.

图11 θ=30°、裂纹尺寸为0.994nm 的(7，7)管的轴压应力－应变曲线Fig.11 Stress-strain curve of (7，7)tube with the crack length of 0.994 nm under axial compression when θ=30°

图12 θ=30°、裂纹尺寸为0.994 nm 的(7，7)管的轴压变形Fig.12 Configurations of (7，7)tube with the crack length of 0.994 nm under axial compression when θ=30°

图13 θ=30°时临界屈曲强度随裂纹尺寸的变化Fig.13 Critical buckling strength vs the crack length when θ=30°

图13 给出了裂纹倾角为30°的(7，7)、(10，10)碳纳米管的临界屈曲强度随裂纹尺寸的变化，由图可知，随着裂纹尺寸增加，其临界屈曲强度降低，在裂纹尺寸由0 增加到1.562 nm 的过程中，(7，7)与(10，10)管的临界屈曲强度分别降低了58.45%及52.48%.

2.2 不同长度含裂纹碳纳米管的轴压屈曲

2.2.1 垂直于轴线方向的裂纹

对管长范围为6 ～30 nm 的含垂直于轴线方向裂纹的(7，7)、(10，10)碳纳米管进行分子动力学模拟，分析其轴压屈曲和后屈曲性能.

图14、15 给出了长度分别为10 及20 nm、裂纹尺寸为0.994 nm 的(7，7)管在轴压过程中的应力－应变曲线及变形形态.与前面管长为6 nm 的管进行对比分析可知，纳米管的弯折同样是首先出现在裂纹处.管长为10 及20 nm 的(7，7)管的轴压屈曲性能的区别不大. 根据势能变化及相应的结构形态(图14(b)及图15(b))可知，碳纳米管的压缩与压杆的屈曲相似，在整体发生屈曲后并没有出现局部的屈曲半波，随着荷载增加，纳米管多处出现弯折.

图14 θ =90°、裂纹尺寸为0. 994 nm、管长为10 nm 的(7，7)管的轴压Fig.14 Curves of stress-strain and potential energy of (7，7)tube with the crack length of 0.994 nm and the tube length of 10 nm under axial compression when θ=90°

图15 θ=90°、裂纹尺寸为0.994nm、管长为20nm 的(7，7)管的轴压应力－应变和势能变化曲线Fig.15 Curves of stress-strain and potential energy of (7，7)tube with the crack length of 0.994 nm and the tube length of 20 nm under axial compression when θ=90°

由图16 可知，对于含垂直轴向裂纹的(7，7)、(10，10)管，随着管长增加，纳米管的临界屈曲荷载呈减小的趋势，管长大于10 nm 后，两种管径的临界屈曲荷载变化都不大.由图16(a)可知，对于裂纹尺寸分别为0.994 和1.562 nm 的(7，7)纳米管，随着管长从6 增加到30nm，其临界屈曲强度的减小量分别为32.8%和25.0%.由图16(b)知，对于裂纹尺寸分别为0.994 和1.562 nm 的(10，10)纳米管，随着管长增加，其临界强度分别减小了11.9%和13.4%.

2.2.2 与轴线方向成30°角的裂纹

本节模拟了裂纹倾角为30°、管长变化范围为6 ～30 nm 的(7，7)碳纳米管的轴压变形行为.

图17、18 给出了管长为10 及20 nm 的(7，7)管的轴压性能.与管长为6 nm 的管进行对比可知，纳米管的凹陷同样是首先出现在裂纹附近区域，裂纹上、下边缘出现扭曲. 管长为10 及20 nm 的含裂纹(7，7)管的轴压屈曲行为相似，由势能变化及结构形态可知，碳纳米管的压缩与压杆的屈曲相似，在整体发生屈曲后并没有出现局部的屈曲半波，随着荷载增加，多处出现弯折，这一整体弯曲现象与裂纹倾角为90°、管长为10 及20 nm 的管相似，但相应的裂纹附近区域的弯曲细节不同. 由图17(a)与18(a)可知，对于裂纹倾角为30°的(7，7)管，随着管长增加，其临界屈曲强度有一定的降低，对于较长的碳纳米管，其呈现压杆屈曲的特性越明显.

图16 含裂纹管的临界屈曲强度随管长的变化Fig.16 Critical buckling strength of tube with crack vs. tube length

图17 θ=30°、裂纹尺寸为0.994nm、管长为10nm 的(7，7)管的应力-应变和势能变化曲线Fig.17 Curves of stress-strain and potential energy of (7，7)tube with the crack length of 0.994 nm and the tube length 10 nm under axial compression when θ=30°

图18 θ=30°、裂纹尺寸为0.994nm、管长为20nm 的(7，7)管的应力－应变和势能变化曲线Fig.18 Curves of stress-strain and potential energy of (7，7)tube with the crack length of 0.994 nm and the tube length of 20 nm under axial compression when θ=30°

3 结论

运用分子动力学方法，研究了含不同裂纹的(7，7)、(10，10)碳纳米管的轴压屈曲行为，分别分析了裂纹尺寸及管长变化对扶手椅型纳米管轴压屈曲性能的影响，得到了相应的应力－应变曲线及变形形态图.结果表明，随着裂纹尺寸增加，含裂纹碳纳米管的临界屈曲强度明显降低.对于裂纹倾角为90°的纳米管，在轴压荷载作用下，裂纹区域内凹，并呈现一定程度的错位现象;对于裂纹倾角为30°的纳米管，随着荷载增加，裂纹附近区域出现凹陷，在裂纹的上下边缘出现扭曲. 对于含两种倾角裂纹的纳米管，在整个轴压过程中，裂纹附近区域的凹陷不再会发生回弹. 随着管长增加，含裂纹碳纳米管的轴向承载力同样减小. 对于裂纹倾角为90°、裂纹尺寸为0.994 nm 的(7，7)和(10，10)碳纳米管，在管长从6 增加到30 nm 的过程中，其临界屈曲强度分别减小了32.8%及11.9%.另外由纳米管相应的变形形态可知，裂纹倾角变化也会影响纳米管结构的压缩行为.

［1］Iijima S. Helical microtubules of graphitic carbon ［J］.Nature，1991，354(6348):56-58.

［2］Ebbesen T，Takad T. Topological and SP 3 defect structures in nanotubes［J］.Carbon，1995，33(7):973-978.

［3］Yakobson B I，Brabec C，Bernholc J. Nanomechanics of carbon tubes:instabilities beyond linear response ［J］.Physical Review Letters，1996，76(14):2511-2514.

［4］辛浩.石墨烯/碳纳米管力学性能的研究［D］. 广州:华南理工大学土木与交通学院，2010.

［5］Hirai Y，Nishimaki S，Mori H，et al. Molecular dynamics studies on mechanical properties of carbon nano tubes with pinhole defects ［J］. Japanese Journal of Applied Physics，2003，42(6S):4120.

［6］Huq A，Goh K，Zhou Z，et al. On defect interactions in axially loaded single-walled carbon nanotubes［J］. Journal of Applied Physics，2008，103(5):054306.

［7］Zhang Y，Xiang Y，Wang C.Buckling of defective carbon nanotubes ［J］. Journal of Applied Physics，2009，106(11):113503.

［8］Ang K，Kulathunga D，Reddy J. In buckling of defective carbon nanotube［C］∥Proceedings of the International Conference on Computing in Civil and Building Engineering.［S.l.］:Nottingham University Press，2010.

［9］Kulathunga D，Ang K，Reddy J.Molecular dynamics analysis on buckling of defective carbon nanotubes［J］.Journal of Physics:Condensed Matter，2010，22 (34):345301.

［10］Chowdhury S C，Haque B Z，Gillespie Jr J W，et al.Molecular simulations of pristine and defective carbon nanotubes under monotonic and combined loading［J］.Computational Materials Science，2012，65:133-143.

［11］Vijayaraghavan V，Wong C. Temperature，defect and size effect on the elastic properties of imperfectly straight carbon nanotubes by using molecular dynamics simulation［J］.Computational Materials Science，2013，71:184-191.

［12］Kinoshita Y，Kawachi M，Matsuura T，et al.Axial buckling behavior of wavy carbon nanotubes:A molecular mechanics study［J］.Physica E:Low-dimensional Systems and Nanostructures，2013，54:308-312.

［13］Eftekhari M，Mohammadi S，Khoei A R.Effect of defects on the local shell buckling and post-buckling behavior of single and multi-walled carbon nanotubes［J］.Computational Materials Science，2013，79:736-744.

［14］Stuart S J，Tutein A B，Harrison J A.A reactive potential for hydrocarbons with intermolecular interactions ［J］.The Journal of Chemical Physics，2000，112(14):6472-6486.

［15］Hoover W G. Canonical dynamics:equilibrium phasespace distributions ［J］. Physical Review A，1985，31(3):1695.

［16］Nosé S. A unified formulation of the constant temperature molecular dynamics methods ［J］. The Journal of Chemical Physics，1984，81(1):511-519.

［17］Swope W C，Andersen H C，Berens P H，et al. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules:application to small water clusters［J］. The Journal of Chemical Physics，1982，76(1):637-649.