改进的三相四线制有源电力滤波器谐波电流检测*

王裕 谢运祥

(华南理工大学 电力学院，广东 广州510640)

随着电力电子技术的快速发展，各种非线性功率器件广泛应用，大量谐波和无功功率注入电网，造成系统效率降低，功率因素变差，严重影响电网和用电设备的安全运行［1］.有源电力滤波器(APF)通过向电网注入与原有谐波电流大小相等方向相反的补偿电流，可以补偿电网的谐波，提高电能质量，增强电网的可靠性和稳定性，其良好的性能在国内外引起了广泛关注［2］.

APF 是通过谐波电流检测电路检测到负载电流中的谐波分量作为参考电流，控制逆变器中开关管的通断，产生相应的补偿电流注入电网中，抵消负载电流中的谐波分量，从而抑制负载电流中的谐波分量注入电网，以免造成谐波污染［3］.为了实现APF 的功能，必须对谐波电流检测环节进行合理设计，实时准确地检测出谐波电流［4］.目前常用的谐波检测法有基于瞬时无功功率理论［5］的p-q-r 法、ip-iq 法［6］、FBD 法［7］、离散傅立叶变换法［8］、自适应谐波检测法［9］等.

基于瞬时无功功率理论的检测方法以瞬时无功功率理论为基础，在工程应用中受到了极大关注.对于三相四线制电容中分式APF，该方法能够对零轴电流进行单独提取补偿，并能对上、下电容电压进行均压控制，增加了补偿的灵活性.但该方法存在复杂的Park 变换、Clark 变换及两者的反变换，计算量很大，增加了软件的开销，降低了检测的实时性［10］.FBD 法是近年国外学者新提出的一种时域检测方法.该方法把实际电路中的各相负载等效为串联在各相的电导，根据等效电导对电流分解，可计算出需要补偿的电流分量，其物理意义明确，实时性好，适用于单相、三相三线制和三相四线制系统的电流检测［11］.虽然FBD 法没有进行复杂的坐标变换，乘法器和触发器的数量远少于瞬时无功功率法，但是该方法运用到三相四线制APF 上时需要先剔除零序电流分量再进行计算［12］，增加了计算的复杂性，且目前并没有文献对FBD 法对三相四线制电容中分式APF 的上、下电容均压控制进行探讨，补偿灵活性没有瞬时无功功率法好［13］.而且，以上两种方法都用到低通滤波器，使得检测存在延时，检测结果和实际值有一定的误差.

基于上述分析，为了克服传统谐波检测方法的不足，更快速有效地检测出谐波电流，文中在分析传统瞬时无功功率理论和FBD 法的基础上，将两种方法相结合，取长补短，提出一种改进的谐波检测方法.该方法前半部分采用FBD 法，减少了传统瞬时无功功率法中因坐标变换引起的矩阵运算，降低了运算量，提高了谐波检测的实时性，通过推导证明剔除零序电流分量是不必要且可省略的，进一步降低了算法的复杂性和运算量.算法的后半部分采用瞬时无功功率理论方法，对零轴电流进行单独提取补偿，并能对上、下电容电压进行均压控制，克服了传统FBD 算法中无法对零轴电流进行单独控制，也不能直接对电容中分式APF 的上、下电容进行均压控制的缺陷，补偿欠缺灵活性的不足，保证了在三相四线制电容中分式APF 的适用性.采用改进的移动平均值算法代替低通滤波器，避免低通滤波器采样和计算过程中产生的滞后误差，提高谐波检测的检测精度.通过仿真和实验，验证了所提出方法的可行性与优越性，对于提高谐波检测精度和动态特性，改善APF 补偿效果具有实际意义.

1 改进的谐波检测方法

1.1 改进谐波检测方法的结构

设三相参考电压为

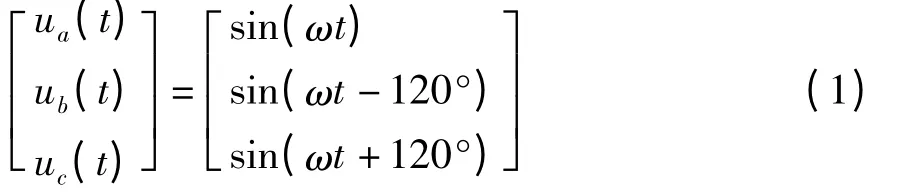
用下标1、2、0 分别表示三相四线制系统中正序、负序、零序电流，则三相电流可表示为正序电流、负序电流以及零序电流之和，即

基于三相系统瞬时无功功率理论的p-q、ip-iq和dqo 旋转坐标法在有源电力滤波器谐波检测中得到了有效的应用，较常用的是ip-iq法［14］.ip-iq检测方法运用在三相四线制APF 中，利用锁相环(PLL)产生与a 相电压Ua同相的正弦和余弦信号，通过Clark 变换和Park 变换，得到ip(t)、iq(t)、io(t).经过坐标变换后，系统的零轴电流io可以单独提取出来，进行均压环控制作用.运算过程为

其中，

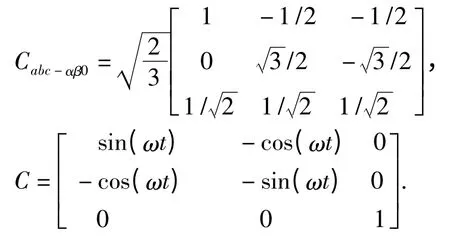
传统FBD 检测方法的有功等效电导和无功等效电导定义如下［15］:

式中，‖u‖2、P∑(t)分别为瞬时总电压和瞬时功率.将三相电压和三相电流代入式(4)，得

经过低通滤波器后分别得到有功电导和无功电导的直流电导分量Gp和Gq，进一步可得到基波正序有功和无功电流.将三相基波正序有功电流分量和无功电流分量分别相加，可得三相基波正序电流分量.用三相负载电流减去基波正序电流分量，既为所需的补偿分量，即

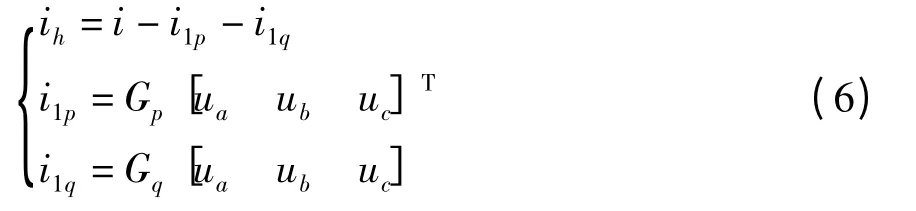
通过对比式(3)和(5)，可以发现瞬时无功功率法中的有功和无功分量ip(t)、iq(t)分别是FBD 法中有功电导和无功电导Gp(t)、Gq(t)的和倍，即

从而，可以根据此关系将两种谐波检测方法进行结合.算法的前半部分采用FBD 法，由三相负载电流ia(t)、ib(t)、ic(t)与三相参考电压作用得到等效电导Gp(t)、Gq(t)，然后根据式(7)的线性变换关系转化为id(t)、iq(t).相比而言，采用改进算法减少了因坐标变换引起的矩阵运算，大大减少了计算量，降低了软件开销，保证了较好的实时性.算法的后半部分采用瞬时无功功率法，将前半部分计算得到的id(t)、iq(t)经过提取直流分量i1d、i1q后，再用ip、iq减去直流参考分量得到交流分量i*p、i*q，稳压环PI 调节器产生的有功电流增量ΔId叠加到谐波检测环节中的有功电流参考值i*p上，上、下电容均压环PI 调节器产生的零轴电流增量ΔIo叠加到谐波检测环节中零序电流参考值i*o中，保证APF 直流测与交流测的能量交换，实现直流测电压和上下电容电压平衡的控制，克服了传统FBD 法无法直接对三相四线制电容中分式APF 的上、下电容进行均压控制的不足.最终得出的有功和无功电流参考量i*p、i*q与补偿零轴电流的指令信号i*o一同经过反Park 和反Clark 变换，得到参考指令电流i*ac、i*bc、i*cc.

1.2 零序电流的处理

为了减小不对称电压对电流检测的影响，不直接使用三相电压来求取功率和等效电导，而是通过锁相环(PLL)来生成与三相电网电压基波同相位的参考电压，使得电流检测结果中不包含电压幅值，因而电压畸变或不对称对检测结果无影响.

将FBD 算法运用到三相四线制APF 中，通常先将三相电流中的零序电流剔除［12，16］，这会增加算法的复杂性和不稳定性.现尝试不将零序电流分离，直接将三相电流代入FBD 算法的计算中，即将式(1)、(2)代入式(5)可得其有功电导:

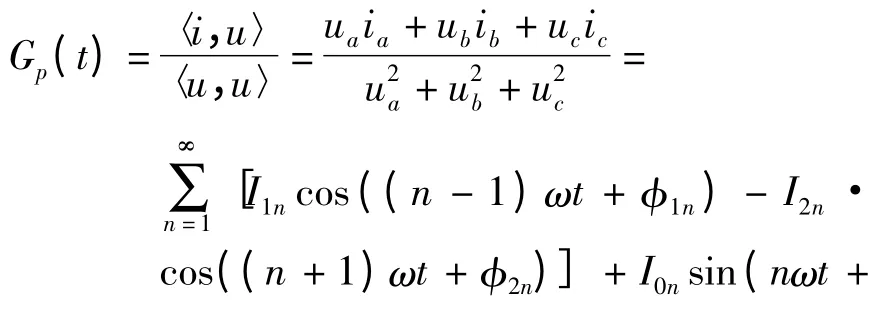
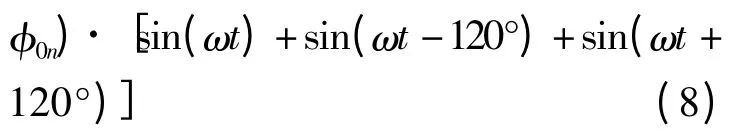
因为sin(ωt)+sin(ωt -120°)+sin(ωt +120°)=0，所以I0nsin(nωt +φ0n)［sinωt +sin(ωt -120°)+sin(ωt+120°)］=0，由此计算出的有功等效电导Gp与式(5)所得出的结果相等.

同样，将式(1)、(2)代入式(5)可得无功电导:

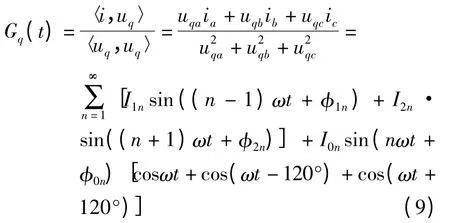
因为cos(ωt)+cos(ωt -120°)+cos(ωt +120°)=0，所以I0nsin(nωt +φ0n)［cos(ωt)+cos(ωt -120°)+cos(ωt+120°)］=0，由此计算出的无功等效电导Gq也与式(5)计算的结果相等.

由以上分析可知，将三相电流代入计算后，其零序电流可抵消为零.所以，FBD 算法运用到三相四线制APF 时，可不必先剔除零序电流，由此可避免计算复杂化，保持算法的简洁和稳定.

1.3 改进的移动平均值法取代低通滤波器

在传统谐波检测方法中，用于提取直流量的低通滤波器的采样和计算过程会产生滞后误差，影响谐波检测精度［17］.为了提高检测精度和提高动态响应速度，文中采用改进的移动平均值法来替代传统的低通滤波器提取直流分量.

在进入直流分量提取单元之前，d 轴信号的直流量对应负载的基波有功功率，q 轴信号的直流量对应负载的基波无功功率.对于dq 轴上的交流分量，其一个工频周期内的所有采样点累加的和为0.而对于直流分量，在一个工频周期内进行所有采样点累加后除以采样点数，结果仍然为该直流信号.

根据以上性质，设每工频周期采样N 个点，通过对这N 个采样点的值进行累加后取一次平均值，即可得到直流分量.但在APF 中，每工频周期取一次平均值的方法不能实时地反映信号的变化.当采样第k 点时，改进的移动平均值法用当前最新的采样信息id(k)代替上一个周期内N 个采样点中最旧的信息id(k-N).即有:

式中，id(k)为当前时刻的新数据，id(k -N)为上一个周期内N 个采样点中最旧的数据.每次采样一次数据，就重新计算一次直流分量，移动平均值随之发生变化.由此，只需要一个采样点的新数据就可以计算出新的输入信号直流分量，在理论上只需要延时一个采样周期，从而保持直流分量根据实际情况实时变化，体现了数据更新的快速性和实时性.

1.4 改进检测算法与传统检测算法特性比较

1.4.1 计算量

传统瞬时无功功率方法在测量出系统电压和电流之后，需要使用36 个乘法器和8 个除法器来决定三相参考电流，计算量很大，而FBD 法没有复杂的Park 变换和Clark 变换，只需要使用18 个乘法器和2 个除法器来决定三相参考电流，且公式中正余弦量均可通过查询正余弦表得到，算法简单，计算量小.因此，通过式(7)的线性变换关系，在算法的前半部分用FBD 法代替瞬时无功功率法，可减少因坐标变换引起的矩阵运算，大大降低算法的运算量，减轻软件的负担，保证了算法良好的实时性.通过推导证明剔除零序电流分量是不必要且可省略的，进一步减小了算法的复杂性和运算量，降低系统的软硬件成本.

1.4.2 上、下电容均压环的控制

虽然FBD 法没有进行复杂的坐标变换，计算量远少于瞬时无功功率法，但它并没有对零轴电流进行单独提取，也不能直接对电容中分式APF 的上、下电容进行均压控制，补偿灵活性没有瞬时无功功率法好.而改进的检测算法后半部分采用瞬时无功功率法，利用其可以通过对零轴电流进行单独控制的特点，将上、下电容均压环PI 调节器产生的零轴电流增量ΔIo叠加到谐波检测环节中零序电流参考值i*o中，实现直流侧上、下电容电压平衡的控制，克服了传统FBD 算法中无法直接对电容中分式APF的上、下电容电压进行均压控制，补偿欠缺灵活性的不足，解决了上、下电容电压平衡的问题.

1.4.3 实时性

由于改进的检测算法前半部分用FBD 法取代传统无功功率法，减少了空间坐标变换，使用的乘法器及除法器个数远比传统的无功功率法少，运算量大大减小，因此改进谐波检测法的实时性相对于传统的无功功率法要更为优越.另外，由于改进的检测方法采用了改进的移动平均值法代替低通滤波器，每采样一个数据就重新计算一次直流分量，只需一个采样点的新数据就可以计算出新的输入信号直流分量，节省软件存储空间，进一步减小软件负担，在理论上只需延时一个采样周期，并且在一个工频周期内，采样点数越多，延时越小，实时性越好.

1.5 改进检测算法总体框图

文中所提出的谐波检测方法总原理框图如图1所示.基于传统的无功功率法和FBD 法应用在电容中分式APF 上的优缺点，推导出两者的内在联系，将两者结合，取长补短.前半部分采用FBD 法，并省去了不必要的零序电流分离环节，由三相负载电流ia(t)、ib(t)、ic(t)与三相参考电压作用得到等效电导Gp(t)、Gq(t)，然后根据线性变换关系转化为id(t)、iq(t)，降低了算法的复杂性，减少了计算量，保证了良好的实时性.后半部分采用瞬时无功功率法，可对零轴电流进行单独提取，直流侧电压和上下电容均压环产生的电流增量分别叠加到谐波检测环节的电流参考值i*p和i*o中，保证了直流测电压稳定和上下电容电压的均衡，确保在三相四线制电容中分式APF 的可行性.采用改进的移动平均值算法代替低通滤波器，避免低通滤波器采样和计算过程中产生的滞后误差，提高了谐波检测精度.

图1 改进的谐波检测法原理框图Fig.1 Block of improved harmonic detected method

2 仿真与实验验证

为了验证所提出算法的可行性和优越性，运用动态仿真软件Matlab 建立的仿真模型进行了仿真分析.同时，搭建了一台33 kW 的三相四线制电容中分式并联有源电力滤波器，在该平台上进行了算法的实验验证.

2.1 仿真验证

运用动态仿真软件Matlab 建立的三相四线制APF 模型进行了仿真实验，仿真参数如表1所示.

表1 系统参数Table1 System parameters

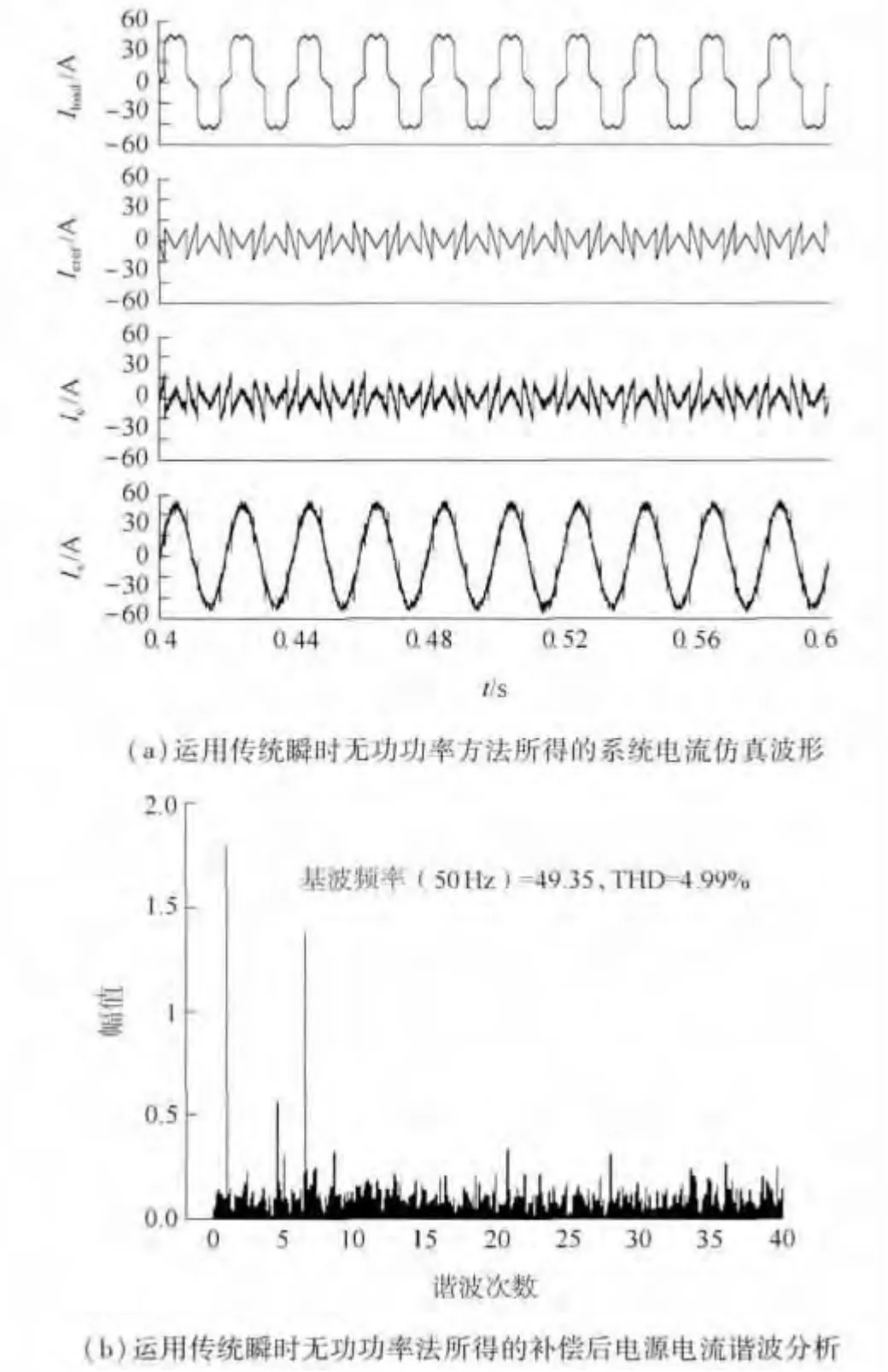
图2 两种检测方法的系统电流仿真波形Fig.2 Simulated current waveform using two detect method

图2为分别运用传统瞬时无功功率算法以及改进的谐波检测算法得出的系统负载电流、输出指令电流、输出补偿电流和补偿后的电源电流波形.由图可以看出，文中所提出的谐波检测算法能准确检测出负载谐波电流，以此作为APF的输出指令电流，电源电流经APF 输出电流补偿后接近正弦，其总谐波畸变率(THD)由补偿前的23.88%下降到补偿后的3.81%，比运用传统瞬时功率检测算法的补偿效果4.99%更好.由此说明，运用改进的谐波检测算法，使得APF 能更精确的检测系统谐波，在相同的电流控制器作用下，具有更好的补偿性能.

为了验证改进谐波算法的动态响应性能，在0.2 s时刻给负载并联一个R=15Ω 的电阻使负载突变.在负载电流突然变大的情况下，将改进的谐波检测算法与传统的谐波检测算法进行比较.图3为当负载发生突变时，分别采用两种检测算法的系统负载和谐波指令电流波形.由图可见，传统的瞬时无功功率算法得到的指令电流需要经过3 个周波才能到达新的稳态，而采用改进的谐波检测算法得到的指令电流只需经过2 个周波就能到达新的稳态.由此说明，采用改进的谐波算法能更迅速的跟上负载的突变，更实时准确地检测出谐波电流的变化，具有更好的动态响应性能.

2.2 实验验证

为了进一步验证该方法的正确性和相对于传统谐波检测算法的优越性，搭建了一台33 kW 的三相四线制电容中分式并联型APF 进行实验验证.为保持仿真和实验的一致性，APF 样机系统参数与仿真一致.检测方法分别为改进的谐波检测法和传统瞬时无功功率法，直流侧电压环和均压环均采用PI控制，电流控制采用基于PI 与重复控制并联的控制策略［18］.

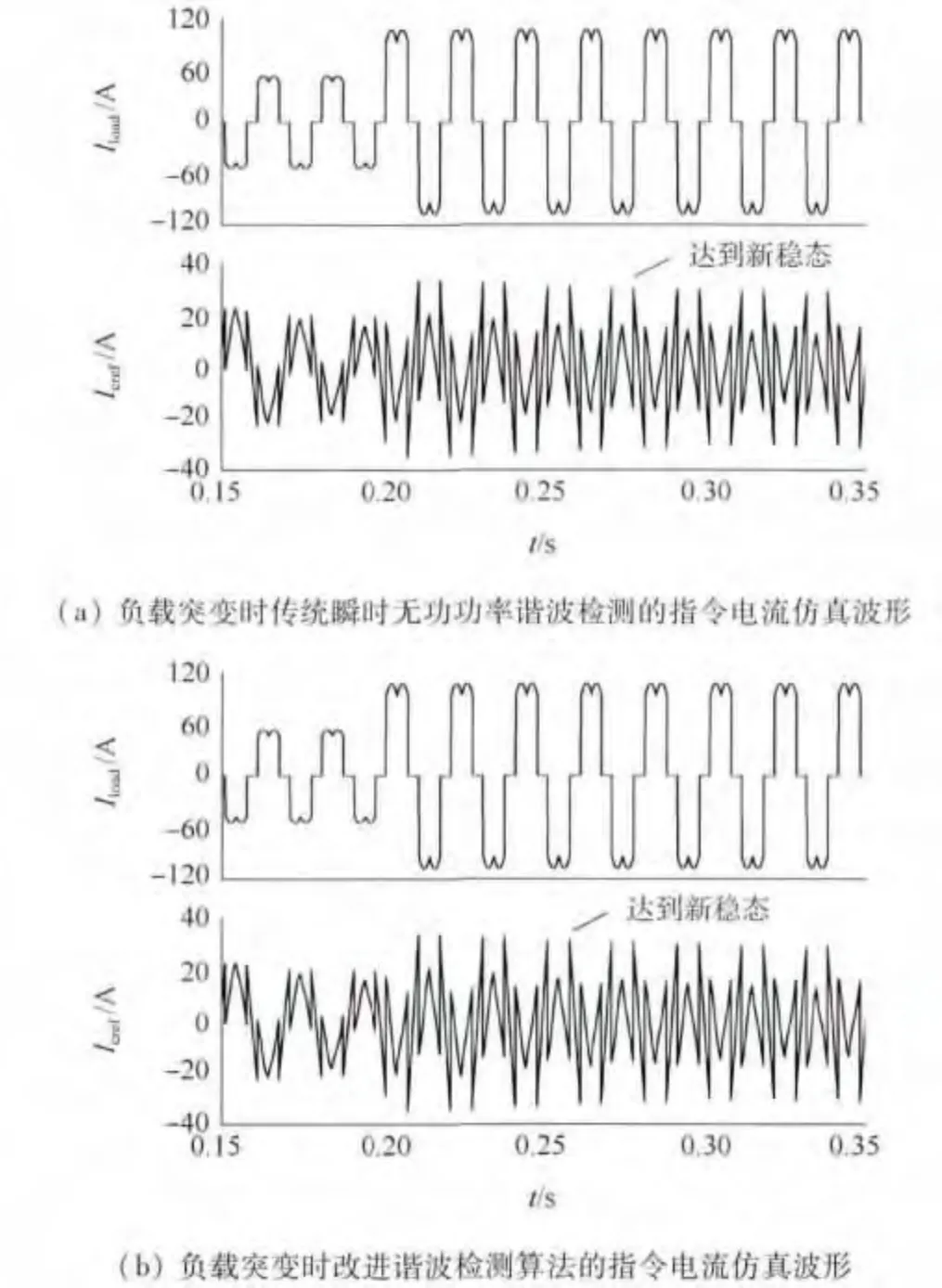
图3 负载突变时指令电流仿真波形Fig.3 Simulated current waveform when load changes

图4为采用改进的谐波检测算法时系统的电压和电流波形.由图可看出，运用改进的谐波检测算法，通过谐波检测算法形成的APF 直流测电压环和均压环均能正常工作，APF 直流侧电压很好地稳定在预设的750 V，上、下电容电压平衡且均为375 V，波动很小，达到直流侧电压稳定控制的目的.以谐波检测算法得出的谐波电流为指令，APF 输出的补偿电流很好地补偿了系统谐波，电源电流经补偿后接近正弦波，其THD 值由24.45%降至4.53%，比运用传统瞬时功率检测算法的补偿效果5.85%更好，补偿后电源电流在换相处的尖峰更小，进一步改善了电源电流质量，达到国标标准.

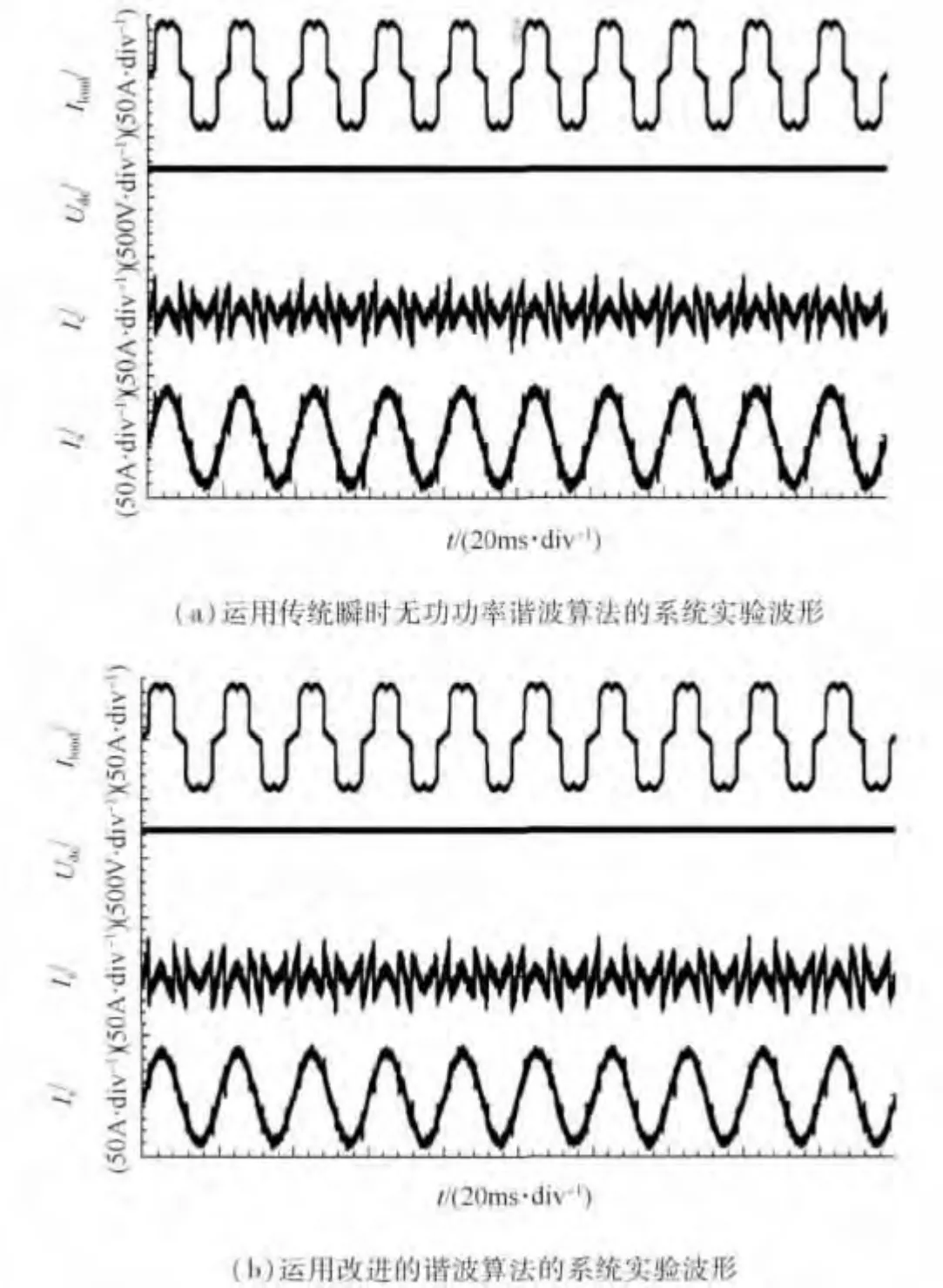
图4 稳态时系统实验波形Fig.4 System experimental waveforms

图5为当负载发生突变时，分别采用传统瞬时无功功率算法和改进的谐波检测算法的系统电流波形.由图可见，采用传统瞬时无功功率谐波检测算法，输出补偿电流因负载突变产生较大的波动，补偿后的电源电流在波峰处产生小幅畸变，而采用改进的谐波检测算法，输出的补偿电流因负载突变产生的波动较小，能更快到达新的稳态，且补偿后的电源电流在波峰处波形更佳，电流换相处的尖峰更小，补偿效果更好.由此，采用改进的谐波检测算法，能更实时准确的检测出谐波电流的变化，具有更好的动态响应，保证有源滤波器在采用相同的电流控制器的情况下，APF 的输出能更迅速的跟上谐波变化，更准确高效的补偿系统谐波，具有更好的动态性能.

图5 负载突变时系统实验波形Fig.5 Experimental waveform when load suddenly change

3 结论

针对传统瞬时无功功率和FBD 谐波检测算法的不足，为了更快速有效的检测出有源电力滤波器中的谐波电流，在分析传统瞬时无功功率理论和FBD 法的基础上，将两种方法相结合，提出一种改进的谐波检测方法.该方法省去了不必要的零序电流分离环节，降低了算法的复杂性.减少了传统瞬时无功功率算法因坐标变换引起矩阵运算，大大减少了计算量，降低了软件开销，并保证了良好的实时性，提高了谐波检测的动态性能.对零轴电流进行单独提取，并对上、下电容的均压进行控制，克服了传统FBD 算法中无法直接对电容中分式APF 的上、下电容进行均压控制，补偿欠缺灵活性的不足，确保算法在三相四线制电容中分式APF 中的可行性.采用改进的移动平均算法代替低通滤波器，避免低通滤波器采样和计算过程中产生的滞后误差，提高了谐波检测精度.所提出的方法对于提高谐波检测性能，改善有源滤波器补偿效果具有实际意义，并可在此基础上进一步探索在三相四线制四桥臂APF 中的应用与改进.

［1］李战鹰，任震，杨泽明.有源滤波装置及其应用研究综述［J］.电网技术，2004，28(22):40-43.Li Zhan-ying，Ren Zhen，Yang Ze-ming.Survey on active power filter devices and their application study［J］.Power System Technology，2004，28(22):40-43.

［2］Singh B，Al-Haddad K，Chandra A.A review of active filters for power quality improvement ［J］.IEEE Transactions on Industrial Electronics，1999，46(5):960-971.

［3］陈国柱，吕征宇，钱照明.有源滤波器的一般原理及应用［J］.中国电机工程学报，2000，20(9):17-21.Chen Guo-zhu，Lü Zheng-yu，Qian Zhao-ming.The general principle of active filter and its application［J］.Proceedings of the CSEE，2000，20(9):17-21.

［4］丁祖军，郑建勇，胡敏强，等.FBD 算法电流检测的滞后误差建模［J］.电工技术学报，2008，23(2):133-137.Ding Zu-jun，Zheng Jian-yong，Hu Min-qiang，et al.Modeling of the delay Error of current detection based on FBD algorithm［J］.Transactions of China Electro Technical Society，2008，23(2):133-137.

［5］王丽，刘会金，王陈.瞬时无功功率理论的研究综述［J］.高电压技术，2006，32(2):98-103.Wang Li，Liu Hui-jin，Wang Chen.Summary of the instantaneous reactive power theory ［J］.High Voltage Engineering，2006，32(2):98-103.

［6］谢运祥，陈坤鹏，邓衍平，等.改进型谐波与基波有功和无功电流检测［J］.华南理工大学学报:自然科学版，2005，33(4):15-19.Xie Yun-xiang，Chen Kun-peng，Deng Yan-ping，et al.Improved detecting method for harmonic and fundamental active and reactive currents［J］.Journal of South China University of Technology:Natural Science Edition，2005，33(4):15-19.

［7］Liu Wenye，Luo Longfu，Zhang Zhiwen，et al.Harmonic current detection algorithm based on the improved FBD method and its application in active power filters［C］∥Power and Energy Engineering Conference.Asia-Pacific:APPEEC，2012:1-5.

［8］周柯，罗安，汤赐，等.一种大功率混合注入式有源电力滤波器的工程应用［J］.中国电机工程学报，2007，27(22):80-86.Zhou Ke，Luo An，Tang Ci，et al.High-power hybrid injection active power filter’s engineering application［J］.Proceedings of the CSEE，2007，27(22):80-86.

［9］张俊敏.基于改进型自适应算法的谐波检测及其性能研究［J］.电力自动化设备，2011，31(4):23-27.Zhang Jun-min.Harmonic detection based on improved adaptive method and its performance study ［J］.Electric Power Automation Equipment，2011，31(4):23-27.

［10］周柯，罗安，夏向阳，等.一种改进的谐波检测方法及数字低通滤波器的优化设计［J］.中国电机工程学报，2007，27(34):96-101.Zhou Ke，Luo An，Xia Xiang-yang，et al.An improved harmonic current detecting method and digital low-pass filter's optimized design［J］.Proceedings of the CSEE，2007，27(34):96-101.

［11］Yang Chao，Huang Qing-xiu，Zhou Jiang-man.Research of hybrid active power filter based on FBD Method detection［C］∥IEEE AIMSEC.［S.l.］:IEEE，2011:4205-4208.

［12］刘宏超，吕胜民，张春晖，等.采用FBD 电流检测法的三相四线APF［J］.电力自动化设备，2010，30(1):45-48.Liu Hong-chao，Lü Sheng-min，Zhang Chun-hui，et al.Three-phase four-wire APF based on FBD-method current detection ［J］.Electric Power Automation Equipment，2010，30(1):45-48.

［13］陈娟，郑建勇，丁祖军，等.p-q-r 法与FBD 法在三相四线制系统谐波电流检测中的对比［J］.电力自动化设备，2007，27(11):30-33.Chen Juan，Zheng Jian-yong，Ding Zu-jun，et al.Comparison of harmonic detection in three-phase four-wire system between p-q-r method and FBD method ［J］.Electric Power Automation Equipment，2007，27(11):30-33.

［14］Ding Zu-jun，Sen Wang，Zhen Guo，et al.Study on hysteresis error and dynamic performance of ip-iq harmonic detection algorithm ［C］∥IEEE AIMSEC.［S.L.］:IEEE，2011:4383-4386.

［15］丁祖军，郑建勇，胡敏强，等.基于优化FBD 算法的谐波与闪变综合抑制装置的应用与研究［J］.电力自动化设备，2008，28(9):19-22.Ding Zu-jun，Zheng Jian-yong，Hu Min-qiang，et al.Harmonic and flicker suppression device based on optimized FBD algorithm［J］.Electric Power Automation Equipment，2008，28(9):19-22.

［16］Dong Ming-xuan，Huang Zhi-hao，Wu Jian，et al.Study on three-leg-based three-phase four-wire shunt active power filter［C］∥IEEE 7th International Power Electronics and Motion Control Conference.［S.l.］:ECCE，2012:552-556.

［17］王群，姚为正，王兆安.高通和低通滤波器对谐波检测电路检测效果的影响研究［J］.电工技术学报，1999，14(5):1-10.Wang Qun，Yao Wei-zheng，Wang Zhao-an.A study about influence of high and low pass filters on detecting effect of harmonics detection circuits［J］.Transactions of China Electro Technical Society，1999，14(5):1-10.

［18］Aurelio García-Cerrada，Omar Pinzón-Ardila，Vicente Feliu-Batlle.Application of a repetitive controller for a three-phase active power filter ［J］.IEEE Transactions on Power Electronics，2007，22(1):237-246.