致密油体积压裂缝网扩展模型建立与应用

2014-10-18程远方王光磊李友志

特种油气藏 2014年4期

程远方，王光磊，2，李友志，时贤，徐鹏

(1.中国石油大学，山东青岛 266580;2.中石化胜利石油管理局，山东东营 257017;3.中海油研究总院，北京 100027;4.中油勘探开发研究院，北京 100083)

引言

中国致密油气等非常规资源储量丰富[1－3]。水平井和体积压裂是致密油等非常规能源进行有效开采的关键技术[4]。体积压裂技术是以大排量泵入低黏度压裂液，在地层中形成以主裂缝为主干，多条分支缝与主缝相通的复杂裂缝网络系统[5－9]。传统水力压裂裂缝几何尺寸计算模型都是基于双翼对称裂缝理论，只适用于计算单一裂缝形态，无法有效模拟复杂缝网的扩展规律及获得最终几何形态参数，因此，需要建立专门的缝网扩展模型来模拟体积压裂缝网扩展规律。

1 缝网扩展数值模型

假设缝网由一条主裂缝及多条不规则分布的次生缝组成。用2簇分别垂直于最大、最小水平主应力方向的平行缝簇表征不规则次生缝，并以水平井筒及主裂缝为中心对称分布(图1)。图1中:a为主裂缝半缝长，m;b为缝网在Y方向的最大延伸半缝长，m;dx、dy分别为垂直于X轴、Y轴的次生缝缝间距，m;σh、σH分别为最小、最大水平地应力，MPa。

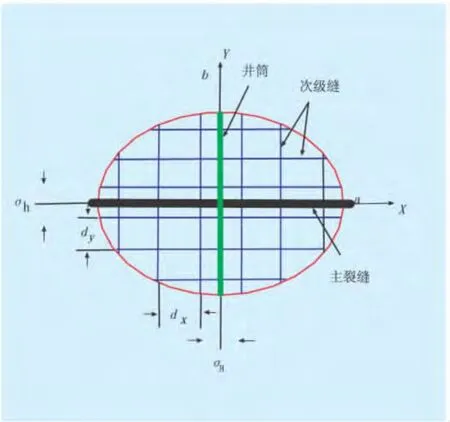
图1 缝网几何形态示意图

1.1 主裂缝拟三维扩展模型

通过调研传统裂缝扩展模型的相关资料[10]，认为主裂缝在地层中满足拟三维裂缝扩展规律，并作出如下假设:①储层为连续性弹性体，具有很大的厚度，裂缝只在储层内扩展;②以恒排量注入压裂液，压裂液在裂缝中沿缝长方向一维流动，流动方式为层流;③主裂缝为垂直于井的水平段的横断缝，以井筒为轴心对称分布;④不考虑支撑剂的铺设及温度对压裂液性质的影响。

1.1.1 连续性方程

假设压裂液不可压缩，则在体积压裂过程中，注入地层的压裂液一部分充填主裂缝，一部分充填次生缝，剩余的滤失到地层中。根据质量守恒原理可知，用于充填主裂缝的压裂液体积与主裂缝体积相等，即:

式中:qD为充填主裂缝的流量，m3/min;t为施工时间，min;VD主裂缝体积，m3。

1.1.2 压降方程

主裂缝的横截面为椭圆形，根据Nolte对平行板缝中的流体流动的压降方程，引入管道形状因子Φ(n')，则幂率流体在主裂缝中某一位置处的压降梯度为:

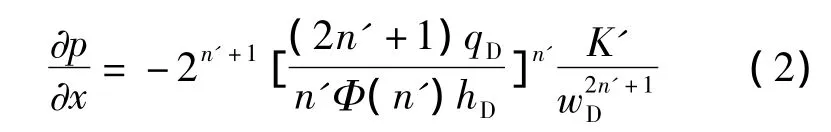
式中:n'为幂率流体的流态指数;Φ(n')为形状因子，在本模型中近似取为3π/16;hD为主裂缝缝高，m;K'为幂率流体的稠度系数，Pa·sn＇;wD为主裂缝缝宽，mm。

1.1.3 缝宽方程

将裂缝沿缝长方向分成若干段，则任意裂缝垂直剖面均可依照平面应变问题求解裂缝宽度。假设主裂缝只在储层内扩展，则对England和Green公式进行简化可获得计算主裂缝缝宽的表达式:

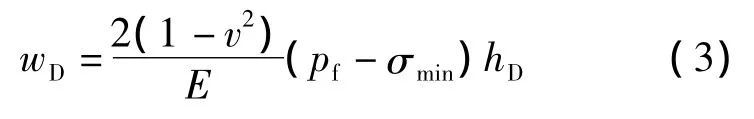
式中:v为储层泊松比;E为储层弹性模量，MPa;pf为主裂缝流体压力，MPa;σmin为储层最小水平主应力，MPa。

因为主裂缝的横截面是椭圆形，缝宽在缝高及缝长方向上的分布均满足椭圆公式，为了之后模型计算的方便，用平均缝宽表征主裂缝缝宽，其表达式为:

1.1.4 缝高方程

根据断裂力学裂纹延伸准则建立计算裂缝高度的控制方程。由线弹性断裂力学的理论可知，裂缝尖端应力强度因子KI1为:

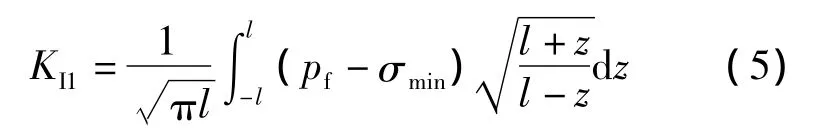
式中:KI1为应力强度因子，MPa·m1/2;l为半缝高，m。

由断裂力学可知，当裂缝尖端应力强度因子达到裂缝断裂韧性时，裂缝开始扩展，即:

式中:KIC1为裂缝的断裂韧性，MPa·m1/2。

联立式(4)和式(5)可得主裂缝高度控制方程:

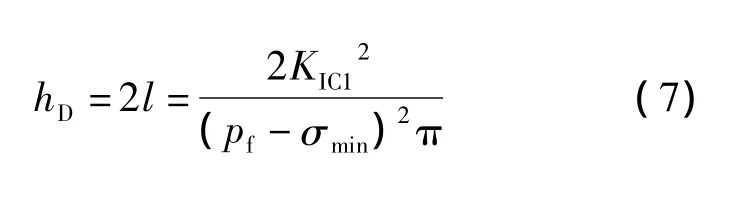
1.2 次生缝几何形态计算模型

利用拟三维扩展模型获得主裂缝的半缝长a、缝高hD、缝宽wD等几何形态参数，参考模拟区块历史压裂设计方案，设定次生缝缝间距dx、dy，椭圆形纵横比γ和次生缝缝宽与主裂缝缝宽的比值λx、λy。基于主裂缝几何形态以及设定的次生缝与主裂缝之间的几何关系，可以获得次生缝几何形态的表达式。

利用缝间距与椭圆半轴长的关系可得次生缝条数的表达式，即:

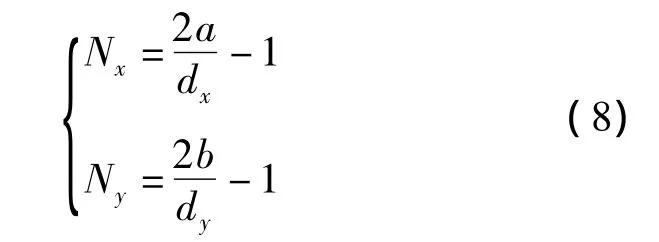
式中:Nx、Ny分别为垂直于X轴、Y轴的次生缝条数;b为椭圆半短轴长，大小为γa，m。

次生缝的总缝长为所有次生缝缝长之和，根据次生缝的位置以及主裂缝缝长，可得:

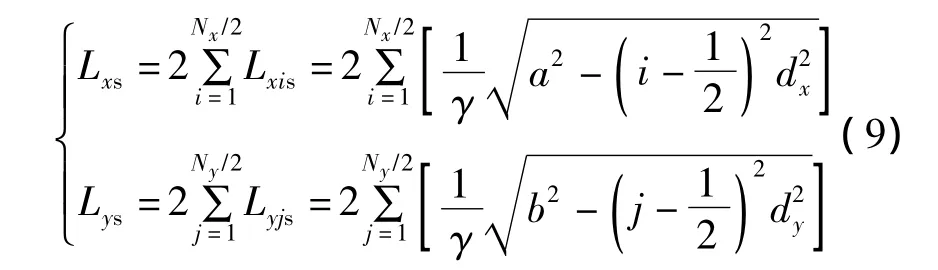
式中:Lxs、Lys分别为垂直于X轴、Y轴次生缝的总缝长，m;Lxis为垂直于X轴第i条次生缝的长度，m;Lyjs为垂直于Y轴第j条次生缝的长度，m。

根据设定的次生缝缝宽与主裂缝缝宽的关系，在已知主裂缝缝宽的前提下，可获得次生缝缝宽的表达式，即:

式中:wxs、wys分别为垂直于X轴、Y轴的次生缝缝宽，mm;λx、λy分别为垂直于 X 轴、Y 轴的次生缝缝宽与主裂缝缝宽的比值。

本模型所模拟的缝网的压裂改造体积为椭球体，次生缝缝高的分布与主裂缝缝高之间满足椭圆关系公式，即:

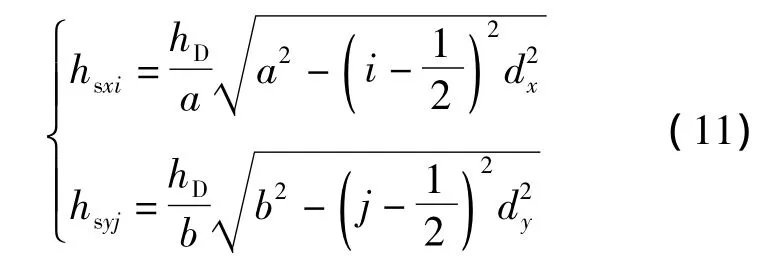
式中:hsxi为垂直于X轴第i条次生缝的缝高，m;hsyj为垂直于Y轴第j条次生缝的缝高，m。

用具有相同a、b的椭柱体体积等效所述椭球体体积，可获得缝网的平均缝高为:

则次生缝网的裂缝壁面面积及体积的表达式为:

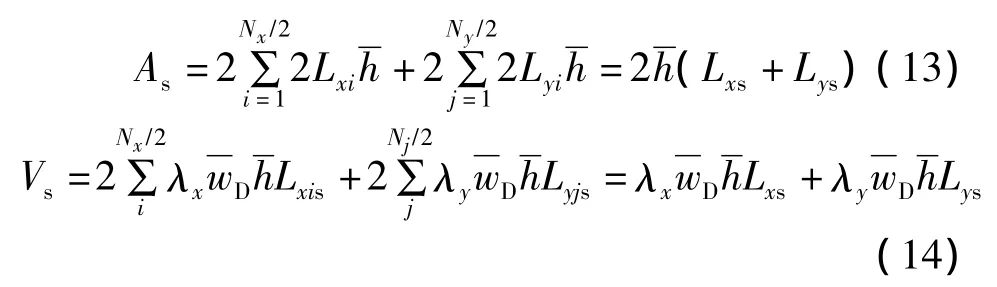
式中:As为次生缝壁面面积，m2;Vs为次生缝体积，m3。

1.3 缝网内压裂液滤失计算模型

假设在缝网主裂缝及次生裂缝的壁面均有压裂液的滤失，且两者滤失系数相同。利用压裂液滤失计算经典理论获得针对于缝网的压裂液滤失计算公式:

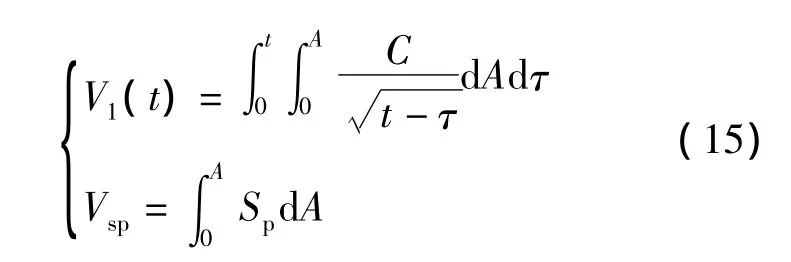
式中:Vl为缝网压裂液滤失体积，m3;A为缝网总面积，大小为主裂缝壁面面积与次生缝壁面面积之和，m2;C为压裂液滤失系数，m·min－1/2;t为压裂施工时间，min;τ为压裂液开始滤失时间，min;Vsp为主裂缝中压裂液初滤失体积，m3;Sp为初滤失系数，m3/m2。

利用主裂缝拟三维扩展模型获得主裂缝壁面面积，利用次生缝几何形态计算模型获得次生缝壁面面积，在给定滤失系数及初滤失系数的前提下，利用式(15)即可求得体积压裂过程中压裂液在缝网中的滤失总量。

2 缝网扩展数值模型的求解

主裂缝扩展模型、次生缝几何形态计算模型和压裂液滤失计算模型之间是相互联系的，并可用质量守恒方程进行最终约束，即:

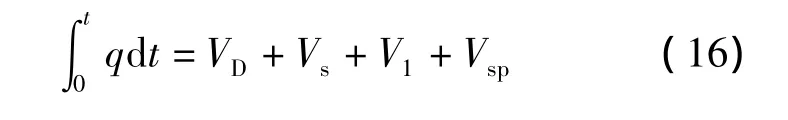
获取压裂液在主裂缝和次生缝中的分配关系是求解缝网扩展模型的关键。因此，首先假设注入主裂缝中的压裂液排量为qD，以时间间隔Δt对压裂施工时间离散，并利用四阶龙格－库塔方法迭代求解出主裂缝几何形态参数、压力及流量分布;其次，基于次生缝几何形态与主裂缝几何形态的关系，求得次生缝几何形态参数;然后利用式(15)求得压裂液在缝网中的滤失体积;最后用式(16)质量守恒方程验证所假设qD的准确性，并获得缝网扩展规律及最终几何形态参数。

3 缝网扩展数值模型的应用

以长庆油田某水平井A井为例。A井是陕北区块长7段水平开发井，水平段垂深为2054 m，水平段长934 m。地层渗透率约为0.21×10－3μm2，孔隙度为10.1%，岩石弹性模量为23.5 GPa，泊松比为0.22，最小水平地应力为32 MPa，最大水平地应力为39 MPa，水平应力差为7 MPa。

对A井共进行了10级压裂，在此以第5段压裂为例，利用缝网扩展模型计算压裂后缝网几何形态参数。设计以8 m3/min的排量泵入567.8 m3清洁压裂液及65.9 m340～70目陶粒。参考该区块历史压裂设计方案及天然裂缝发育程度，设定次生缝缝间距dx为10 m，dy为10 m，椭圆形纵横比为0.3，次生缝缝宽与主裂缝缝宽的比值 λx为0.8，λy为 0.8。

利用缝网扩展模型计算，A井第5段压裂后所获压裂改造体积延伸长度为511.8 m，延伸宽度为153.5 m，缝网中所含裂缝的平均缝宽为1.70 mm，总缝网平均缝高为41.8 m(表1)。通过微地震监测获得的缝网形态参数与模拟计算结果进行对比，表明模型模拟结果与实际微地震监测结果具有良好的一致性(表2)。