基于自适应模糊逻辑的活塞发动机TCU故障检测算法研究
2014-10-11熊云涛唐荣澳刘爱兵
熊云涛,唐荣澳,刘爱兵
(1.中航工业洪都,江西南昌330024;2.电子科技大学航空航天学院,四川成都611731)
0 引言
开展活塞发动机TCU地面试车及故障诊断研究,对于确保试飞安全具有重要意义。发动机故障自动检测本质上属于模式识别问题[1],即通过计算机自动完成复杂的数据分析工作,实现发动机状态的分析与判断。近年来,现代故障检测理论和算法不断完善和拓展,建立了基于信号处理、统计、人工智能等的多种故障检测新理论和新方法[2-3],包括:模糊逻辑法、频谱分析法、状态模型辨识法、随机模型参数法、专家系统法等。[4-5]
为检测发动机运行状态及故障分析,本文通过分析模糊逻辑系统的数学原理及其自适应学习算法,引入模糊逻辑算法,建立了基于模糊逻辑的故障诊断方法,并利用MATLAB软件实现了该模块功能,经分析获得了一些参考结果,为实现对发动机TCU运行状态监控与分析奠定了基础。
1 自适应模糊逻辑数学原理
设备故障检测存在着不确定性,这种不确定主要表现在随机性和模糊性两个方面[7]。随机性是由于事物的因果关系不确定造成的。模糊性是指事物在质上没有确切的含义,在量上没有明确的界限,造成亦此亦彼的性态。为了解决在设备检测中存在的逻辑和数值上的逻辑性现象,采用了模糊数学的描述方法。模糊数学在精确数学的基础上进行了延伸和推广,能够描述事物的不确定性现象。

以上所述模糊集合是针对某单个论域而言的。当将论域扩展至N个论域时,形成了一种模糊关系。这种模糊关系表现为N个集合的叉积。假设有N个论域:X1,X2…,XN, 则定义在U=X1×X2×…×XN上的模糊集称为X各元素间的N元模糊关系。简记为关系式(4)。 隶属度函数简记为(5)。
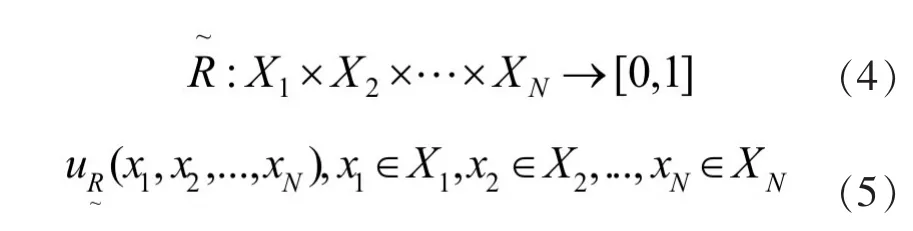
当论域数N=2时,二元模糊关系式(6)被称为从X1到X2的模糊关系。若论域中元素个数是有限值,如,,则模糊关系可以表示为模糊矩阵,如式(7)。

在模糊关系中,每一个模糊元组都有一个介于0与1之间的隶属度,表示该元组隶属于该关系的程度。隶属度还可以表示为式(8)。则在论域X1和X2中,隶属函数可表示为(9)。符号“◦”为模糊集上的广义模糊算子,包括Zadeh算子、概率算子、有界算子、ν算子等。其中,在自适应模糊逻辑系统的设计中,使用T算子作为模糊隶属度的计算规则。T算子的计算过程如式(10)。

模糊关系描述了两个论域之间的隶属度关系,利用这个关系集可完成由论域空间模糊集到另一空间模糊集的映射。自适应模糊逻辑系统既是实现从输入空间模糊集向输出空间模糊集的映射。在模糊关系中,每个模糊规则确定了一个定义于输出空间的模糊集,其隶属函数可表示为(11)。
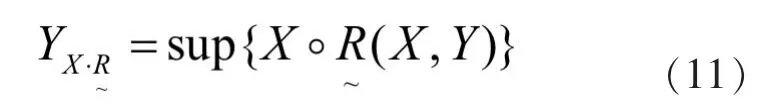
在模糊逻辑系统中,系统输出是逻辑运算的结果,对应的是精确值,所以还需完成模糊集到确定值之间的映射,这一过程是反模糊化。一般情况下,对输出进行反模糊化的运算采用式(12)所示的规则。由此可以证明,式(12)所示的模糊逻辑系统可以任意精度逼近非线性函数f。
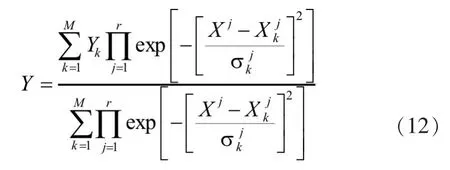
在获取系统的非线性输入输出数据后,确定模糊逻辑系统,以使其以任意精度逼近原系统输入输出,这就是模糊逻辑系统的构造问题。自适应模糊逻辑系统的构造采用学习算法实现。
定义训练数据对(Xp,Yp),及误差函数如式(13),自适应模糊系统的学习就是调整模糊系统的结构及参数,使得误差J最小。经典的方法是最速下降法,如式(14)所示。
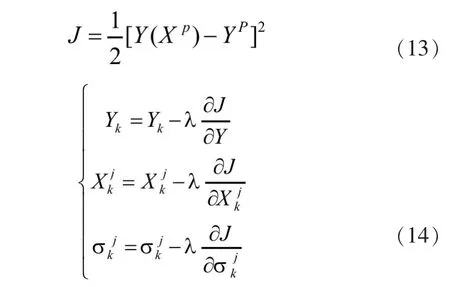
令
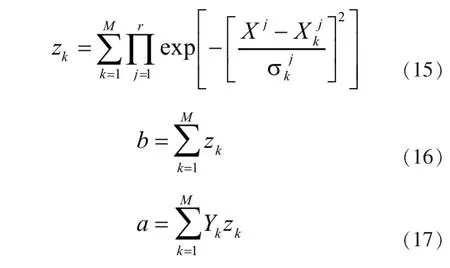
由式(14)推导可得,最速下降法的数学描述如式(18)所示。

最速下降法的学习在临近局部最小误差时容易出现震荡,使性能下降。为减小学习震荡对系统学习性能的影响,采用了“惯性项”的方法,如式(19)。


2 基于自适应模糊逻辑的故障检测算法设计
在利用自适应模糊逻辑算法设计某型发动机故障检测系统时,需首先确定系统输入和能够体现发动机工作状态的输出参数。将发动机系统输入/输出参数归纳如表1所示。表中整理了与发动机工作状态密切相关的参数,参数中某个输入参数发生变化可能导致发动机状态的变化,体现为输出参数的变化。在输入/输出栏,给出了参数的输入输出性质,若一个参数可以作为预测系统的参考输入值则其具有输入属性;若一个参数可作为发动机工作状态的特殊体现,则其具有输出属性,有的参数兼具有输入和输出两个属性。在状态描述栏中主要描述了参数的作用和所体现的发动机状态。

表1 参数属性列表
若将表1中除转速外的所有具有输入属性的参数作为输入量XIN,发动机转速作为输出量YAN。设计观测器系统f,输入输出关系如式(21)所示。

模糊系统的构建按3个步骤展开:模糊化、模糊规则构建、反模糊化。
模糊化运算既是将输入空间U向定义在U上的模糊集的映射,如式(22)所示。将输入向量XIN中各向量分别定义为模糊集
。首先对输入向量进行归一化操作,规则如式(23)。设计隶属度函数,如图1所示,选用高斯函数,将空划分为若干模糊子集。即将输入空间映射到了模糊集上,假设n=8。
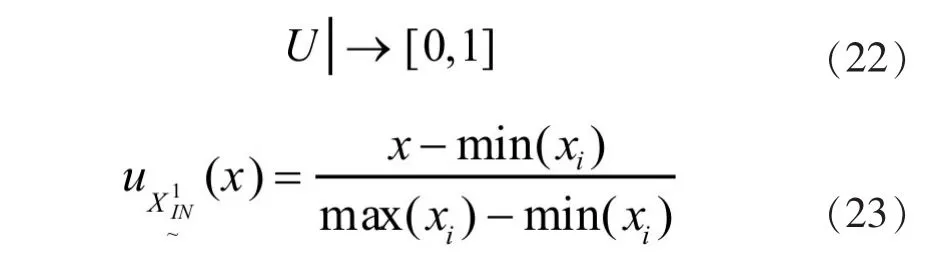

图1 隶属函数
构建模糊逻辑系统的第二步操作是构建模糊规则库。模糊规则库由一组模糊规则构成,构建模糊规则库的过程即是求解隶属度矩阵的过程。由于自适应模糊逻辑系统具有自学习的能力,可以使用随机矩阵通过学习算法得到准确的模糊矩阵。其目的是实现到输出空间的模糊集的映射。最后是确定反模糊化准则,利用模糊系统输出的模糊集到精确量之间的映射。式(15)描述了改进型中心反模糊化的方法。
自适应模糊逻辑系统的数学模型可表示为式(24),自适应学习算法表示为式(25)。其中Yk是输出对输出论域中第k模糊集的属度,是第k输入参数中第j隶属度函数的对称中心,是第k输入参数中第j隶属度函数的标准差。
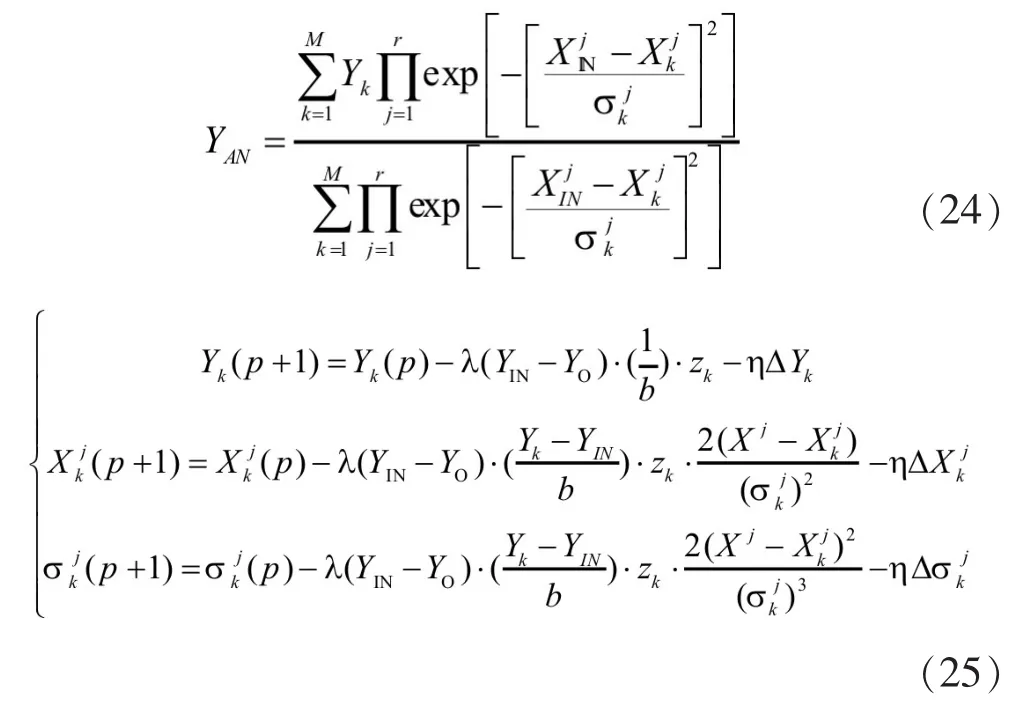
判决器采用窗函数与输出残差的卷积运算实现。设备故障的判定标准为观测器输出与设备实际输出之间残差,且持续时间。构建残差判决函数如式(26)所示,其中H(t-τ)为窗函数,如式(27)。 故障的判决条件如式(28)。
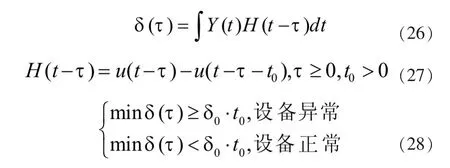
3 算法分析及MATLAB程序实现
基于观测器的故障检测算法,核心在于实现系统的准确建模。对系统性能的分析,集中在影响建模准确性的两个方面:模型的拟合精度和输入完整性。模型拟合精度指模型对非线性函数的拟合效果及其稳定性,输入完整性指系统输入是否能真实反映影响系统状态的量。只有满足两方面的特征,故障检测系统才能正常工作。
建立模糊系统,其输入输出满足式(29)。令x2在区间[0,10]内取值。该模糊系统输入输出关系如图2所示。构建自适应模糊逻辑系统,对f(x)进行模拟。其中,输入输出论域被划分为5个模糊集,隶属度函数分别满足,如图3所示。
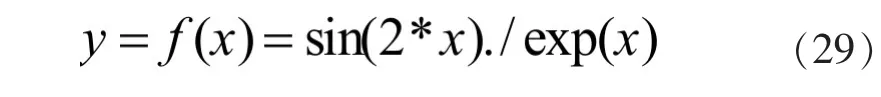
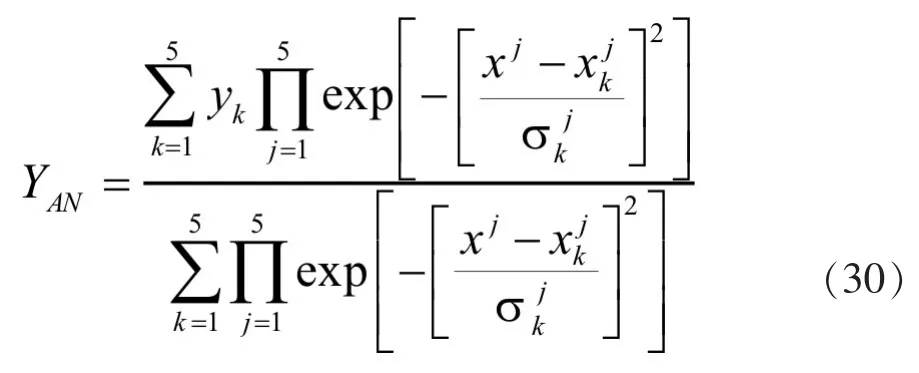
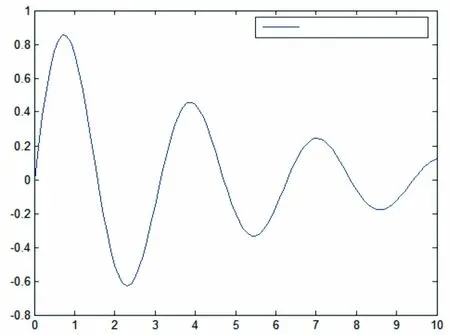
图2 模糊系统输入输出关系

图3 隶属度函数n=5
自适应模糊系统经训练数据的训练,其对系统f(x)输出的线性逼近,如图4(a)所示。该系统经过20次参数调整,均方根误差小于0.042。取输入x∈[2,4],其函数逼近效果如图4(b)所示。可见,自适应模糊系统能够实现对非线性系统的逼近,随着训练次数的增大,误差逐渐减小。
实现对系统建模的另一个关键因素是输入向量真实反映系统的因变量。将某型发动机转速作为系统输出的系统,其输入可以直接等价于油门开度。该发动机某次地面测试数据如图5所示。利用自适应模糊逻辑系统对该关系进行建模,油门作为输入,转速作为输出,模型对系统的逼近如图6所示,误差小于0.015。

图4 自适应系统对f(x)的逼近

图5 速度-油门数据图

图6 模型对速度的逼近
基于MATLAB软件,其模糊逻辑工具箱中,提供了对模糊逻辑算法的支持。典型的自适应模糊逻辑系统是学者Jang Roser提出的ANFIS结构。该结构利用反向梯度下降算法和最小二乘方法来完成对输入、输出数据的建模,相应的MATLAB函数为anfis。本文利用了其构建观测器及其学习能力的程序。
4 结论
活塞发动机地面试车检测系统的故障分析与诊断功能,对于确保试飞安全具有重大意义。本文通过分析模糊逻辑系统的数学原理,研究了基于模糊逻辑的故障诊断模块分析算法,并在MTALAB环境中编程实现了故障诊断模块,经分析获得了一些参考结果,为分析并监测发动机TCU运行状态奠定了基础。
[1]何勇.航空发动机台架试车CAT系统研发:[硕士学位论文],南京:南京航空航天大学,2009:2-3.
[2]屈梁生,张海军.提高故障检测质量的几种方法,中国机械工程,2001,10:1168-1172.
[3]吴昭同,杨世锡.旋转机械故障检测特征提取与模式分类新方法,科学出版社,2012:13-16.
[4]屈梁生.谈谈机组故障的可检测性问题,检测技术,1994,5:22-23.
[5]屈梁生,张海军.机械检测中的几个基本问题,中国机械工程,2000,11(1-2):211-216.
[6]洪涛.液体火箭发动机涡轮泵实时故障检测算法研究:[博士学位论文].成都:电子科技大学,2012,5:33.
[7]吴今培.模糊检测及其理论应用,科学出版社,1995:27-28.
