马尔科夫链推广模型在股指预测中的应用*

孙建英，王显昌，陈建云

（1.青岛理工大学琴岛学院，山东青岛 266106；2.大连海洋大学理学院，辽宁大连 116023；3.德乐生软件有限公司，北京 100020）

马尔科夫链推广模型在股指预测中的应用*

孙建英1，王显昌2，陈建云3

（1.青岛理工大学琴岛学院，山东青岛 266106；2.大连海洋大学理学院，辽宁大连 116023；3.德乐生软件有限公司，北京 100020）

将状态集空间法引入到马尔科夫链预测模型中，并且分析了状态集空间对预测结果的影响.同时将这种新型的马尔科夫推广模型，应用于股指数据的预测问题.发现这种方法不仅符合马氏检验的条件，而且预测的准确率也有所提高.

马尔科夫链；沪深300；状态集空间法；马氏检验

马尔科夫链模型，得名于俄罗斯的数学家安德烈·马尔科夫，是一种非常重要的随机决策模型.它的最显著的特性是：预测时刻的状态只与随机变量当前的状态有关，而与历史状态无关，这种“无后效性”的特点使得该模型广泛地应用在投资决策、桥梁技术、植被变化、股票价格、汇率预测［1－4］等方面，并取得了很多令人满意的成果.

本文引入了状态集，提出了状态集空间法，通过将t个状态作为一个状态，来预测下一个大盘交易日状态的方法，结果是准确率随t的增加大幅上升，这种马尔科夫链推广算法，应用到沪深300样本股2010.1.30－2012.4.5的数据，预测2012.1.31－2012.4.5的股指变化情况，发现这种新方法不仅符合马氏检验的条件，而且预测的准确率也有所提高.

1 马尔科夫链模型

1.1 马尔科夫链的定义

定义1：对离散空间I中的随机序列｛Xn，n＝0，1，2，…，｝若在任意时刻n，以及任意的状态i0，i1，…，in－1，i，j满足：

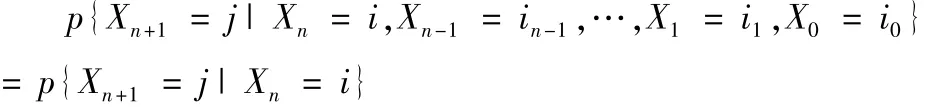
则随机序列｛Xn，n＝0，1，2，…｝即为马尔科夫链，简记｛Xn，n≥0｝．马尔科夫链是最简单的一类马尔科夫过程.

1.2 一步转移概率

定义2：设｛Xn，n≥0｝为一马氏链，条件概率

称为在时刻n的一步转移概率.

由于从状态i出发，经过一步转移以后，必须到达状态空间I的一个状态，且只能够到达一个状态，故一步转移概率pij（n）应满足下列条件：

若马氏链的一步转移pij（n）与n无关，则称此马氏链为齐次马氏链，这时，记pij为元素构成的矩阵

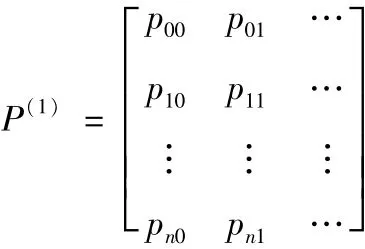
称为一步转移概率矩阵.

若状态空间I是有限集.则称｛Xn，n≥0｝为有限马氏链.

1.3 马尔科夫链预测模型

定理1：设｛Xn，n≥0｝是一个齐次马氏链，具有初始概率分布p0（i），i∈I，且其n步转移概率为p（n）ij，i，j∈I，n≥0，则

式中（1）式表明，在n时刻的绝对概率分布完全被初始概率分布和n步转移概率所确定，式中（2）式就是著名的查普曼－科尔莫格罗夫（Chapman－Kolmogorov）方程，（2）式的矩阵形式即为：

由上式进一步得到：P（n）＝（P（1））n，由此可见，n步转移概率矩阵可由一步转移概率矩阵获得.

2 马尔科夫链推广模型及实证分析

2.1 数据集

数据来源：http：／／www2.resset.cn／product／

训练数据集：沪深300样本股2010.1.30－2012.4.5

预测数据集：沪深300样本股2012.1.30－2012.4.5

2.2 状态集空间法

状态集空间法是将T作为一个状态，用T这个状态来预测下一个大盘交易日的股指期货的变化情况.T＝1，2，3，…，n.

T＝1表示将一天的数据作为初始状态矩阵，再和状态转移矩阵相乘来预测下一交易日的变化情况.T＝2表示，将连续两个大盘交易日的数据作为一个状态，来预测下一交易日的股指期货的变化情况，依次类推.

通过实验分析，T越大，预测准确率也会越大.我们将状态空间分为三个状态，规定大盘指数下降超过20点为大跌，记为3；下降点数在20点到上涨20点之间保持不变，记为2；上涨在20点以上为大涨，记为1.随T变化此方法预测的准确率汇总表见表1（MATLAB6.5）.

表1 状态集空间法预测准确率统计表

由上表我们可见状态集空间法的马尔科夫链对股指的预测有很好的效果，在一定范围内，T越大，准确率越高.

2.3 状态转移矩阵

由状态集空间法，我们研究将连续两天的状态作为初始状态，来预测下一个大盘交易日的涨跌情况.

由初始可能出现的状态1到下一个状态的转移情况，在此状态空间有3*3种情况，在将这两个已知状态作为初始状态预测下一个交易日的状态，共有3*3*3种情况，也就是说状态转移矩阵S为3*3*3的三维矩阵.利用训练数据集，我们求出状态转移矩阵为

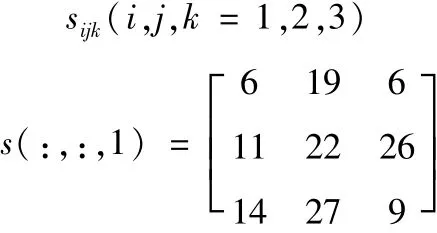
s（：，：，1）表示有已知两个状态转向状态1，即大涨的频数.

s（：，：，2）表示有已知两个状态转向状态2，即保持不变的频数.

s（：，：，3）表示有已知两个状态转向状态3，即大跌的频数.

将上述三个矩阵合起来就是状态转移矩阵.

2.4 状态转移概率矩阵

状态转移概率矩阵也是一步转移概率矩阵，在状态集空间法下，我们把已知的两个状态作为初始状态，来看转向下一状态的概率，由状态转移矩阵分析，我们可知状态转移概率矩阵也为

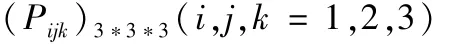
根据概率的性质，有：

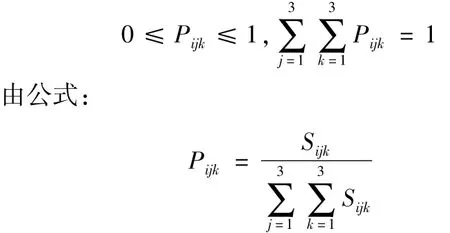
状态转移概率矩阵为：

p（：，：，3）表示有已知两个状态转向状态3，即下跌的概率.

我们对状态转移概率矩阵进行分析，对 p（：，：，1）、p（：，：，2）和p（：，：，3）进行分析，这三个3*3的矩阵对应相同位置表示由已知前两个状态转移到状态1、2和3的概率，且其概率和为1.

由此我们可知相同位置上概率最大的就是前两个状态最可能转移到那个状态，我们取出这三个矩阵中每个位置概率最大的值重新组成一个新矩阵fmax．

由fmax矩阵，我们可以得出前两个状态对应最可能转移到那个状态值，状态值组成矩阵Q．

从而我们可以通过已知的初始状态预测其下一个可能转移的状态.

2.5 数据分析

我们以2012／2／21和2012／2／22日的大盘交易状态为初始状态集对2012／2／23到2012／4／6日的大盘交易的数据进行预测，结果如表2所示.

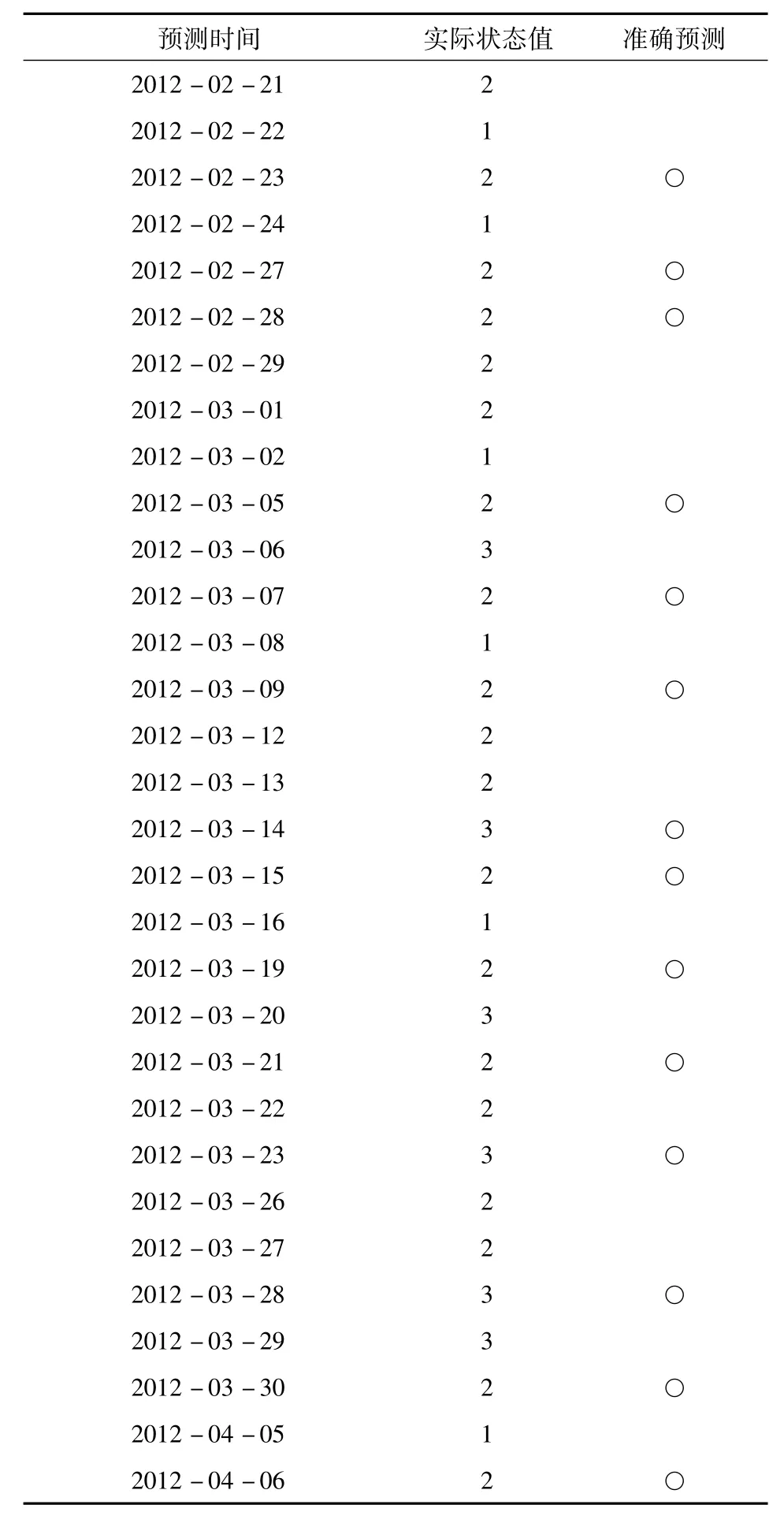
表2 2012.2.21－2012.4.05期间31个大盘交易日的预测状态与实际状态对比

通过统计得出其准确率为50%，其准确率相对较高，说明此种改进的马尔科夫链方法对股指期货的预测效果还是明显的.

2.6 马氏检验

在此我们将马氏检验的公式进行推广：

设nijr（k）表示k期X1，X2，…，Xn从状态集（i，j）经过一步转移到状态k的频数，并记频数矩阵：

在此Pijr表示状态转移矩阵的第（i，j，r）个元素，即由状态i转移到j再转移到r的概率.

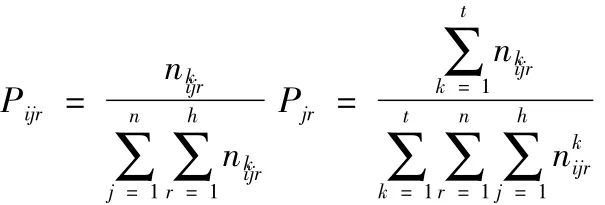
统计量服从自由度为（m－1）（n－1）（h－1）（t－1）的χ2分布.选定置信度α，查表得χ2α（（m－1）（n－1）（h－1）（t－1）），令

3 结论

通过对改进算法进行的马氏检验和准确率分析可知，改进后的算法有可行性，此种算法可以应用到其他经济决策领域中.但是不可否认，马尔科夫链模型只是一种概率预测模型，只是说明未来的一种趋势，而不是绝对的状态.同时状态集的划分和样本容量的大小等都会对预测的准确性有一定的影响，在应用过程中要注意具体问题具体分析，灵活运用.

［1］耿波，王君杰，张谢东.桥梁技术状况预测的灰色马尔科夫链模型研究［J］.武汉理工大学学报，2007，（1）：107－110.

［2］李晖，白杨，杨树华，等.基于马尔科夫模型在怒江流域中段植被动态变化预测［J］.生态学杂志，2009，（2）：371－1376.

［3］刘宗明，贾志洵，李兴莉.基于灰色马尔科夫链模型的交通量预测［J］.华东交通大学学报，2012，（1）：30－34.

［4］陈渝，谢天添，林涛，等.两种马尔科夫链菜单预测模型建模［J］.四川大学学报（自然科学版），2013，（2）：255－260.

（责任编校：晴川）

App lication of M arkov Chain Expansion M odel in the Predication of Stock M arket

SUN Jianying1，WANG Xianchang2，CHEN Jianyun3
（1.Qindao College，Qingdao Technological University，Qingdao Shandong 266106，China；2.College of Science，Dalian Ocean University，Liaoning Dalian 116023，China；3.CRM－factory，Beijing 100020，China）

A new concept of State of Spacemethod is introduced in Markov chain predication model and its effect on predication result is analyzed in this paper.The new method is applied to the predication of stock market.It is not only in conformity with the Markov test，and the prediction accuracy is also improved.

Markov chain；Hu－Shen 300；state of spacemethod；Markov chain test

F064

A

1008－4681（2014）05－0100－03

2014－08－15

孙建英（1979－），女，山东烟台人，青岛理工大学琴岛学院讲师，硕士.研究方向：应用数学.