非线性时滞微分方程组周期解存在的一个充分条件*
2014-10-10翁爱治
翁爱治
(上海政法学院经济管理学院,上海 201701)
非线性时滞微分方程组周期解存在的一个充分条件*
翁爱治
(上海政法学院经济管理学院,上海 201701)
考虑非线性时滞微分方程组周期解的存在性问题,应用Leray-Schauder不动点定理,证明了非线性微分方程组周期解新的存在性结果.
周期解;Leray-Schauder度;非线性
记R为实数集,R+为非负实数集.本文研究非线性时滞微分方程组

的周期解存在性问题,其中x∈Rn,A∈Rn×Rn,τ∈C(R,R+),对任意的t∈R+有τ(t+T)=τ(t),f∈C(R×Rn,Rn)且对任意的t∈R,x∈Rn有f(t,x)=f(t+T,x).
近几年,有不少文献(例如参考文献[1-7])研究时滞微分方程的周期解问题,例如参考文献[1]应用锥不动点定理研究标量方程
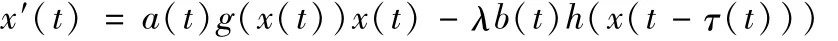
正周期解的存在性.h∈C(R×R,R).参考文献[6]研究如下方程组
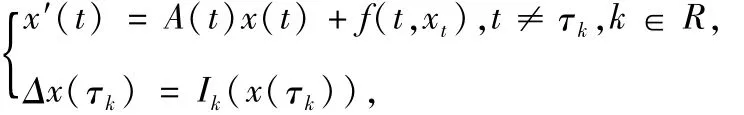
正周期解的存在性问题,其中x∈Rn,A(t)是对角矩阵,即
A(t)=diag{a1(t),a2(t),…,an(t)},对任意的t∈R,要求ai(t)>0,i=1,2,….
这里我们以一个形式简单的方程为例,叙述文献[1-7]中共同的研究方法和条件.考虑方程
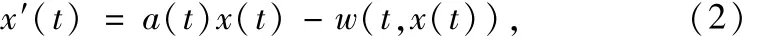
其中x是标量,a∈C(R,R+)是T-周期解,w∈C(R×R,R)关于第一变元是T-周期的.方程(2)是参考文献[1-7]所考虑方程的特殊情况,从而就方程(2)而言,参考文献[1-7]的研究方法和假设条件存在共同点,即定义Banach空间
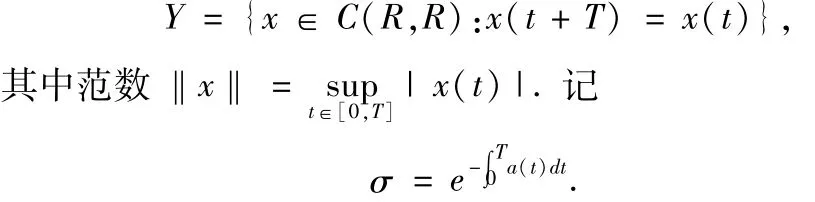

定义锥定义映射Φ:K→Y:
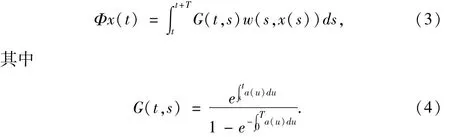
方程(2)的周期解存在性问题转化为Φ的不动点存在性问题.从(3)和(4)式看出条件

是必不可少的,而且以下的两个条件

足以保证Φx>0,从而保证方程(2)的周期解是正的.假设n阶矩阵A的所有特征根均不为零(这个假设条件与(5)式对应),在Banach空间(具体定义见基本引理部分)中定义映射Γ:
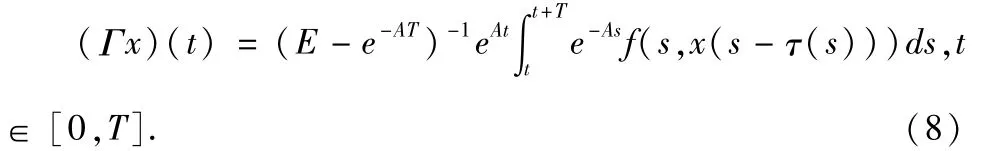
把方程(1)的周期解转化映射Γ的不动点.以方程(1)为研究对象,与(6),(7)式对应的假设条件应为
(i)A的所有特征根都是正的,
(ii)对任意的t∈R,x∈Rn都有f(t,x)>0.
但是这两个条件无法保证Γx>0.本文仅获得方程(1)周期解的存在性,而没能保证周期解的正性.所用的方法为Leray-Schauder不动点定理.关于方程(1)的正周期解,需要进一步的条件,我们将在今后的文章中研究.
1 基本引理
本文将利用下面的Leray-Schauder不动点定理.



以AH表示矩阵A的转置矩阵.若AHA=AAH,则称A为正规矩阵.根据线性代数的知识,A∈Rn×n是正规矩阵的充分必要条件是存在酋矩阵Q使得

本文假设如下的条件成立
(H1)矩阵A是正规矩阵,且所有特征根λi,i=1,2,…,n全不为零,
(H2)存在单调不减函数g:[0,∞)→[0,∞)及正实数r,使得对任意的x∈Rn,只要‖x‖≤r,t∈[0,T],则如下的不等式成立

这里要求r满足不等式

引理2 对任意的x∈X,Γx∈X.
证明 因为f(t,x)是连续函数,所以对任意的x∈X,

从而Γx∈X.证毕
另外,易证Γ:X→X是全连续的.比较(10)和(11)式得Γ的不动点即为方程(1)的周期解.
2 主要结果


(13)式和(15)式矛盾,从而(14)式不成立.根据引理1,Γ在¯U中存在不动点x0,从而x0是方程(1)的一个周期解.证毕.
[1]Wang H.Positive periodic solutions of functional differential equations[J].Journal of Differential Equations,2004,(2):354-366.
[2]Zeng Z,Bi L,Fan M.Existence ofmultiple positive periodic solutions for functional differential equations[J].Journal of Mathematical Analysis and Applications,2007,(2):1378-1389.
[3]Yan J.Existence of positive periodic solutionsof impulsive functional differential equationswith two parameters[J].Journal of Mathematical Analysis and Applications,2007,(2):854-868.
[4]Zhang X,Yan J,Zhao A.Existence of positive periodic solutions for an impulsive differential equations[J].Nonlinear Analysis:Theory,Methods and Applications,2008,(10):3209-3216.
[5]Zhang N,Dai B,Chen Y.Positive periodic solutions of nonautonomous functional differential systems[J].Journal of Mathematical A-nalysis and Applications,2007,(2):667-678.
[6]Bai D,Xu Y.Periodic solutions of first order functional differential equations with periodic deviations[J].Computers and Mathematics with Applications,2007,(9):1361-1366.
[7]Zhang N,Dai B,Qian X.Periodic solutions for a class of higherdimension functional differential equations with impulses[J].Nonlinear Analysis:Theory,Methods and Applications,2008,(3):629-638.
[8]Granas A,Dugundji J.Fixed Point Theory[M].New York:Springer-Verlag,2003.
(责任编校:晴川)
A Sufficient Condition for the Existence of Periodic Solutions of Nonlinear Differential Systems
WENG Aizhi
(Department of Economics and Management,Shanghai University of Political Science and Law,Shanghai201701,China)
This paper deals with the existence of periodic solutions for nonlinear delay differential systems.Some new existence results of periodic solutions for this system are obtained via the Leray-Schauder Nonlinear Alternative.
periodic solution;Leray-Schauder Nonlinear Alternative;nonlinear
O175.14
A
1008-4681(2014)05-0003-03
2014-06-19
上海政法学院院级课题(批准号:sz12015).
翁爱治(1975-),女,福建莆田人,上海政法学院经济管理学院副教授,博士.研究方向:微分方程稳定性理论及应用.
