基于MATLAB的多目标规划最优投资组合方法的探讨*

杨伍梅，刘 权

（1.益阳职业技术学院基础课部，湖南益阳 413049；2.湖南创元电厂，湖南常德 415000）

基于MATLAB的多目标规划最优投资组合方法的探讨*

杨伍梅1，刘 权2

（1.益阳职业技术学院基础课部，湖南益阳 413049；2.湖南创元电厂，湖南常德 415000）

目前投资种类繁多且风险各异，投资者很难选取收益较高而风险较低的可操作性投资组合.针对这一问题，利用多目标规划的方法建立投资组合优化问题的一般模型，在合理假设的基础上将多目标规划问题转化为单目标规划问题，使模型简化更具有可操作性.采用Matlab对实例进行计算，验证了所提方法的可行性和实效性.

多目标规划；最优投资组合；MATLAB；收益；风险

现实投资中，在各类投资的收益和风险各不相同的情况下，投资者希望对收益和风险做出综合分析，找出一种收益最大而风险最小的最优投资组合［1］.与之相关的理论层出不穷，伴随着Matlab优化工具箱的出现，极大地简化了人们对此问题优化算法求解的实现过程［2］.这里介绍一种多目标规划择取最优投资组合的方法［3］，在Matlab平台下编写程序，设计和实现投资组合最优化.

1 多目标规划最优投资组合模型

1.1 理论假设

（1）在一定时期内针对各种投资所给出的平均收益率、损失率、交易费率保持不变［4］.

（2）在一定时期内所购买的各种资产不进行买卖交易.（3）各种投资是否收益是相互独立的.

（4）在投资过程中，不管盈利与否必须付交易费.

1.2 符号说明

M（元）：投资总额；

n：投资种类；

Si（i＝0，1，2，…，n）：购买的第i种投资；其中S0代表存入银行；

xi（i＝0，1，2，…，n）：购买Si的金额；

ri（i＝0，1，2，…，n）：购买Si的平均收益率；r0为存入银行的利率，取值为5%；

qi（i＝0，1，2，…，n）：购买Si的损失率；

pi（i＝0，1，2，…，n）：购买Si超过ui时所付交易费率．

1.3 建立模型

由分析可知，对Si投资的收益为：rixi；对Si投资xi时所付的交易费为C（x），则ii

为简化计算，可假设投资额M相当大［5］，从而对每个Si的投资xi均会超过ui，则（1）式可简化为：

显然，这是一个多目标规划问题，现采用主要目标法，将之转化为单目标最优化问题.

1.4 模型简化和求解

方案一：如果以收益为主要目标，则可固定风险水平［7］，将问题转化成为求最大风险不超过a时的最大收益，对应式（3）的线性规划模型一：

方案二：若投资者希望总盈利超过K，则可在风险最小的情况下寻找最优投资组合［8］，从而转化为如式（4）的线性规划模型二：

2 利用Matlab求解模型、分析结果

为了检验上述两个模型的实用性和可操性，我们针对表1所提供的数据，利用模型一进行求解.

设某公司有笔足够大的资金M用来投资，而目前市场上有n种资产可供选择，相关数据如表1所示.

表1 投资风险与收益表

下面我们利用Matlab对此问题进行求解并进行投资分析.将表中的数据代入模型一中，可以得到Matlab的标准型为：

由于a是任意给定的风险度，为了简化计算，在求解的过程中不妨用试探的方法，从a＝0开始，以步长Δa＝0．001进行搜索，通过实验来分析风险度a和收益Q之间的关系.

相应的Matlab代码如下：

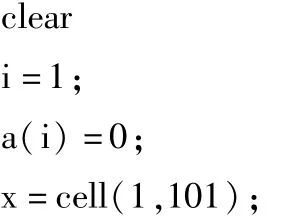
通过运行Matlab程序，可得风险与收益关系图如下：

图1 风险度与收益关系图

图2 图1的局部放大图

分析上述两图：

（1）由图1可知，收益随风险增大而增大.

（2）由数据可以看出，投资者若要降低风险，则需分散投资.

（3）曲线上的每一点都表示该风险水平下最大可能收益和该收益下的最小风险.投资者可根据其风险承受能力，选择该风险水平下的最优投资组合.

（4）由图2可以看出，在a（18）＝0．025附近有一个转折点．在该点左边，风险增加很少时，而利润增长很快；在该点右边，风险增加很大时，而利润增长却很缓慢．所以对于风险和收益没有特殊偏好的投资者来说，应选择该转折点a（18）＝0．025，Q*＝Q（18）＝0．267作为最优投资组合，所对应投资方案为：x＝［0，1，1．6667，0．4545，0．78125，1.7857，0．9615］T．

3 结论

由上述分析可知，利用Matlab求解多目标规划最优投资组合是一种操作简单、结果可靠、计算精度高的方法［9］.此方法采用投资取舍原则，排除了部分项目，将十分复杂的多目标规划问题简化为线性规划求解，在找到合适的解的同时又提高了计算速度和效率.而且采取固定风险求解最大收益的方案，不仅可使求解过程极大简化，也可给投资者多种选择方案，可操作性较强.

［1］任立民，邓芳.投资组合中多目标规划最优化数学模型的应用［J］.海峡科学，2007，（7）：72－75.

［2］李明.详解MATLAB在最优化计算中的应用［M］.北京：电子工业出版社，2011.

［3］方运生.目标规划最优投资组合方法［J］.池州师专学报，2003，（3）：4－6.

［4］马昌凤.最优化方法及其MATLAB程序设计［M］.北京：科学出版社，2010.

［5］石猛，孙静.基于MATLAB的优化工具箱的最优投资方案的设计与实现［J］.现代计算机，2003，（10）：80－82.

［6］曹圆圆，朱孔来.基于MATLAB的证券投资组合优化分析［J］.科技情报开发与经济，2006，（16）：142－143.

［7］李伯德.最优投资组合的数学模型与案例分析［J］.兰州商学院学报，2006，（2）：98－99.

［8］畅文生，黄晓乃，伍衡山，等.模糊数学在采矿方法优化选择中的应用［J］.长沙大学学报，2002，（4）：54－57.

［9］张国辉，赵丽红.紧急物资调运问题的数学模型研究［J］.湖南城市学院学报（自然科学版），2011，（2）：36－39.

（责任编校：晴川）

Study of MATLAB Multi－objective Programm ing Method Based on Optimal Portfolio

YANGWumei1，LIU Quan2
（1.Department of Basic Courses，YiYang Vocational and Technical College，Yiyang Hunan 413049，China；2.Chuangyuan Power Plant in Hunan，Changde Hunan 415000，China）

Currently，there are various different investment risks，so it is hard for investors to select an operational portfolio with high income and low risk.In allusion to this problem，the study utlizes themethod ofmultiobjective programming to setup the generalmodel of portfolio optimization，and on the basis of reasonable hypothesis，themultiobjective programming problem is transformed into a single objective programmingwhich ismore operational.Matlab is used to calculate the example，which has verified the effectiveness and feasibility of the proposed method.

multiobjective programming；optimal portfolio；Matlab；income；risk

O221.6

A

1008－4681（2014）05－0009－03

2014－08－30

杨伍梅（1981－），女，湖南益阳人，益阳职业技术学院基础课部讲师，硕士.研究方向：最优化理论与算法.