求解二维半线性微分方程多解问题的间断Galerkin有限元方法*
2014-10-10杨婧
杨 婧
(湖南农业大学理学院,湖南长沙 410128)
求解二维半线性微分方程多解问题的间断Galerkin有限元方法*
杨 婧
(湖南农业大学理学院,湖南长沙 410128)
结合间断Galerkin有限元和插值系数有限元方法计算二维半线性多解问题,并通过数值例子证实了方法的有效性.
半线性微分方程;多解;间断Galerkin有限元;插值系数有限元
在科学和工程计算中半线性微分方程非常常见,它们往往有多个甚至无穷多个解.对于这些结构复杂的解,尤其是非稳定解,用数值方法进行求解,是一个具有挑战性的重要课题.陈传淼等[1]提出了一种用于计算多解的搜索延拓法,理论上能计算出任意高Morse指标的解,但实际上,当Morse指标很大时,解的图形中含有很多陡峭的峰,数值解容易振荡.
近三十年来,在椭圆方程、对流扩散方程、Hamilton方程、Maxwell方程等问题上取得卓越成效的间断有限元方法[2,3],在解决含有振荡现象的问题中发挥着巨大的作用.间断有限元方法既能保持传统有限元方法的优势,又能克服其不适于间断问题的缺点,对于求解含边界峰和内部峰的解是一个有效的方法[4],所以本文结合插值系数有限元,采用间断有限元方法计算半线性微分方程多解问题.
1 半线性椭圆问题的间断有限元
我们在区域Ω=(0,π)×(0,π)上讨论以下Dirichlet问题
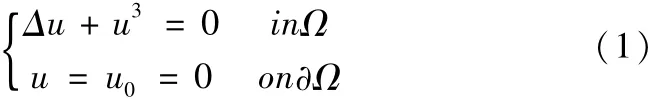
令q=▽u,可将方程(1)改写为

取试探函数v∈L2(Ω),r∈L2(Ω)2,分别与方程(2)中的前两个方程相乘,然后在每个单元上进行分部积分,可得(2)的弱解形式

其中nk是边界上的外法向向量.
记s(k)为对Ω剖分成的矩形网格T上的双线性分片多项式空间,定义有限元空间MN={q∈L2(Ω)2:q|k∈s(k)2,∀k∈T},VN={u∈L2(Ω):u|k∈s(k),∀k∈T},则有限元解qN∈MN,uN∈VN满足弱解形式,且对任意的v∈VN,r∈MN有其中G为五对角块阵,D为对角块阵,U为未知向量.


2 数值例子
我们用前面叙述的间断有限元和插值系数有限元方法实际计算半线性问题(1),最终转化为用牛顿法求解一个非线性方程组(5),故有必要讨论初值的选取.
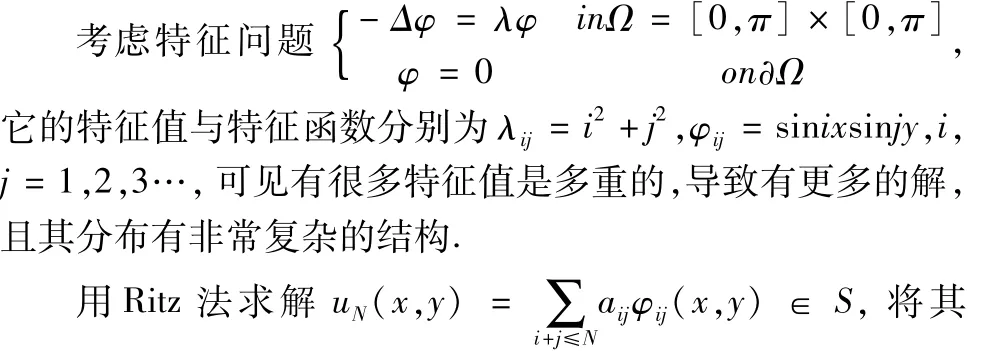


图1 λ11对应的解,N=32
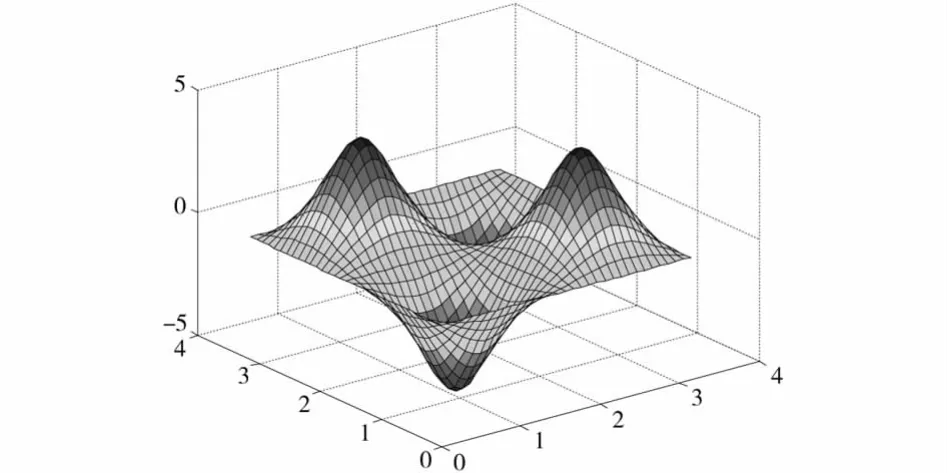
图2 λ22对应的解,N=32

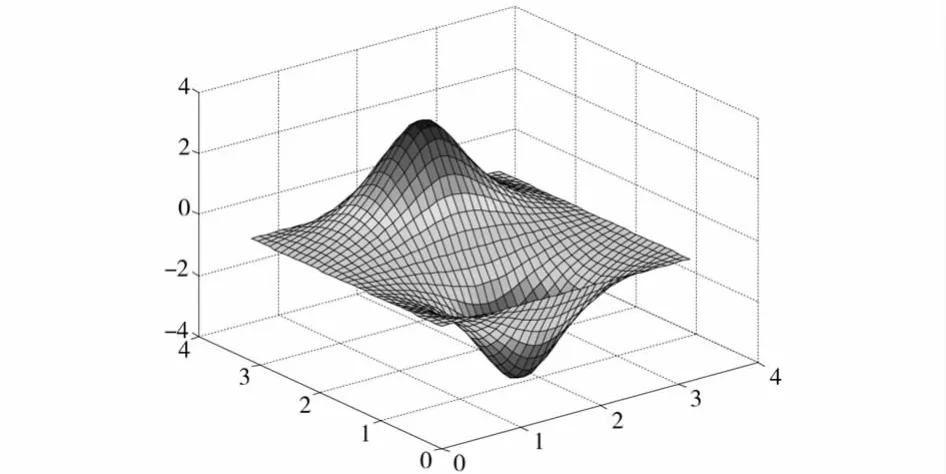
图3 λ12对应的解,N=32
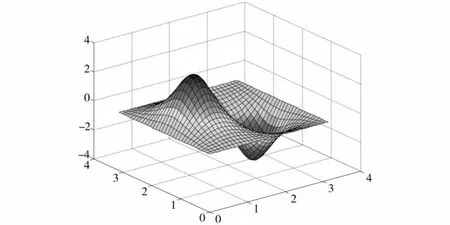
图4 λ21对应的解,N=32
从图中可以看出,间断有限元处理多解问题仍能体现出它的优点,它所计算出来的解没有任何振荡.但间断有限元的缺点是计算量偏大,故可以考虑采用并行算法进行运算.
[1]陈传淼,谢资清.非线性微分方程多解计算的搜索延拓法[M].北京:科学出版社,2005.
[2]Cockburn B,Shu C.The local discontinuous Galerkin method for time-dependent convection-diffusion systems[J].SIAM Journal on Numerical Analysis,1998,(6):2440-2463.
[3]张作政.对流扩散方程间断有限元方法的后验误差估计指[J].长沙大学学报,2012,(2):1-2.
[4]Xie Z,Zhang Z,Zhang Z.A numerical study of uniformsuperconvergence of LDGmethod for solving singularly perturbed problems[J]. Journal of Computational Mathematics,2009,(2-3):280-289.
[5]Xie Z,Chen C.The interpolated coefficient FEM and its application in computing the multiple solutions of semilinear elliptic problems[J].International Journal of Numerical Analysis and Modeling,2005,(1):97-106.
(责任编校:晴川)
The DG M ethod for Solving M ultip le Solutions of Two-dimensional Sem ilinear Differential Equations
YANG Jing
(College of Science,Hunan Agricultural University,Changsha Hunan 410128,China)
In this paper,discontinuous Galerkin finite elementmethod and interpolated coefficient finite elementmethod are combined to solve two-dimensional semilinear problem with multiple solutions.Numerical results are presented to show the efficiency of the method.
semilinear differential equation;mutiple solutions;DGFEM;ICFEM
O241.81
A
1008-4681(2014)05-0001-02
2014-07-09
湖南农业大学青年科学基金(批准号:12QN28)资助项目.
杨婧(1982-),女,湖南长沙人,湖南农业大学理学院讲师,硕士.研究方向:微分方程数值解.
