易拉罐轴向受压失稳试验研究及有限元分析

2014-10-10李魏梓宋昕宜马新玲

制造业自动化 2014年15期

李魏梓，宋昕宜，杨凯，马新玲，杨刚

LI Wei-zi, SONG Xin-yi, YANG Kai, MA Xin-ling, YANG Gang

(华东理工大学机械与动力工程学院，上海 200237)

0 引言

在外压容器进行设计的时候，需要对外压容器的稳定性进行计算与校核[1]。与周向失稳不同的是，薄壁圆筒容器的轴向失稳不遵循线性小挠度理论，而是遵循非线性理论[2]。但是，轴向圆筒的外压实验在本科教学中较难实践，也因此缺乏足够的实验案例，这使得探索合适的实验方法成为了一项值得探究的课题。市面上所生产的330毫升“雪碧”铝制易拉罐(如图1所示)，不仅取材方便，而且符合薄壁圆筒的结构要求，是合适的薄壁圆筒试验模型。另外，为进一步验证轴向失稳非线性理论的适用性[3]，同时也为验证易拉罐模型试验结果的可靠性，还采用ANSYS软件对其轴向失稳的过程进行了有限元法计算与分析[4]，并与试验结果进行了比较和研究。

图1 330ml“雪碧”易拉罐

图2 除去封头与外漆的易拉罐

图3 易拉罐轴向失稳试验装置

图4 易拉罐粘贴应变片并与导线连接

1 外压圆易拉罐薄壁圆筒轴向稳定性试验

试验首先应获得易拉罐的结构数据。使用游标卡尺测得易拉罐的外径D为62.5mm，使用螺旋测微器测得易拉罐的壁厚为0.0945mm，则中径的值可计算得62.4055mm。去除封顶后的圆筒使用直尺测得计算长度为90mm。

对易拉罐圆筒施加轴向外压进行稳定性试验的装置如图3所示，为多功能材料力学实验台和XL2118C电阻应变测试仪[5]。装置主要由支架、操作手轮、加压装置与电阻应变仪组成。试验采用电测法[6]。首先对易拉罐采取封盖去除与外壁除漆的措施，以便轴向外压的施加与应变片的粘贴，处理结果如图2所示。电阻应变片粘贴完成后，如图4所示，通过导线将应变片与电阻应变仪相连，再利用加压装置与垫板将易拉罐轴向对中固定在装置上，至此准备工作完成。然后，将应变仪器的读数清零，转动操作手轮，加压装置不断下降，开始缓慢施加轴向载荷。载荷施加过程中，对应变仪中的应变与压力值进行记录，同时注意观察易拉罐筒壁的变形情况。当载荷施加到一定程度，易拉罐圆筒会发出轻微的“砰”的响声，同时应变仪上的应变值会出现突变，表明此时易拉罐轴向失稳发生，停止加载，并记下此时的压力（临界载荷）。重复上述试验步骤，总共得到10组试验数据，并计算得到试验临界载荷平均值。

表1 试验临界载荷值汇总表

临界载荷值测定完毕后，还需要获得易拉罐的杨氏模量以供试验数据分析和有限元分析。而在轴向受压失稳试验时记录的载荷与应变数据，为杨氏模量的计算提供了原始材料。本试验选择了5组数据的部分试验点作图，纵轴为试验得到载荷换算而来的应力值，横轴为应变仪读得该载荷下的应变值。近似以线性来计算弹性模量。通过Origin软件对图表做线性回归分析，所得到的斜率即为杨氏模量E[7]。其中一组的数据分析图如图5所示。5组数据分析得到的杨氏模量汇总如表2所示，并计算得到杨氏模量试验平均值为74.6182GPa。

表2 实测杨氏模量值汇总表

图5 应力应变实测关系图

在《全息干涉测铝板杨氏模量算法的讨论》[8]一文所给出的可靠数据中，铝材弹性模量的值约为70GPa。本研究的试验计算结果与查得的铝材弹性模量数值接近，并考虑到制造与缺陷的各方面原因，因而可以认为74.6182GPa的试验结果是较为可靠。

2 易拉罐薄壁圆筒的有限元屈曲分析

在ANSYS软件中建立屈曲模型时，需要易拉罐的杨氏弹性模量与泊松比的数据[9]。杨氏模量取为与试验结果相近的75GPa，泊松比一般取0.3[10]。确定杨氏模量、泊松比与其它物性尺寸数据后，采用ANSYS软件建立如下线性与非线性共两个屈曲分析模型。

2.1 线性小挠度理论模型

筒体采用shell 93单元进行模拟，壳单元数为1512，节点数为4748[11]。在筒体一端轴向方向固定，另一端轴向施加10000N/m的受压线载荷。筒体两端的半径方向位移以及切向转角固定，进行特征值屈曲分析，即线性分析。在筒的轴向施加10000N/m的线载荷。有限元计算模型如图6所示。图7是有限元分析后得到的筒体应变与应力分布情况。根据ANSYS有限元软件分析，特征值为1.2818，即临界线载荷q1=1.2818×104N/m。由图7可见，线性理论分析下，筒体的纵向出现波形但在圆周方向无波形。

图6 有限元网格剖分与计算模型

图7 筒体失稳模态（线性理论分析）

2.2 非线性前屈曲理论模型

在线性分析的基础上施加结构缺陷，进行非线性分析。约束与线性分析相同，同时在筒的轴向施加5400N/m的线载荷进行非线性分析，直至模型失稳。ANSYS软件分析完毕后，可由软件绘制出筒体轴向受压的载荷—位移曲线（如图8所示）。当时间t=0.998701时，结构发生了屈曲，此时对应的临界载荷q2=5400×0.998701=5392.99N/m时，结构发生非线性屈曲。显然，图8中载荷与轴向位移并不是线性关系。

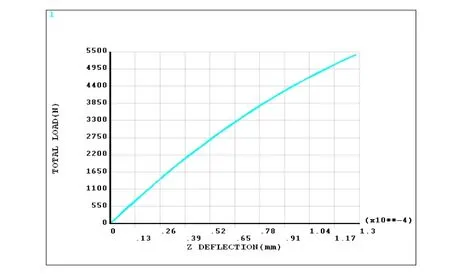
图8 受压载荷与轴向变形分析图表（非线性理论分析）

3 分析讨论

3.1 易拉罐圆筒轴向失稳临界载荷值计算

试验所获得的临界载荷值为1021.6N，如表1所示。《化工容器设计》[12]一书中所给的薄壁圆筒轴向受压失稳的临界压力经验表达式为：

上式中，E为圆筒的杨氏弹性模量，t为圆筒壁厚，R为圆筒外半径。

代入易拉罐的相应物性数据，可求得理论临界应力值：

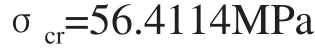
由《材料力学I》[13]一书中所介绍的应力与载荷关系：

求得理论临界载荷值为1045.1N。其中，A是为圆筒壁横截面积。A=π(D2-d2)/4，D为圆筒外径，d为圆筒内径。

在ANSYS有限元软件分析中，线性理论分析得到的特征值为1.2818，即临界线载荷q1为1.2818×104N/m，由式(3)：

求得临界应力σr1=135.6402MPa。式中dm为圆筒中径。而同样由上式，取非线性分析结果中临界线载荷q2=5392.99N/m，求得临界应力σr2=57.0687MPa。。根据σr1与σr2，计算得基于线性理论与基于非线性理论的临界载荷值F1与F2分别为2513.0N与1068.8N。所有临界载荷值计算结果汇总如表3所示。

3.2 线性理论与非线性理论的正确性

从失稳形态上看，所有试验中失稳的易拉罐由于壁厚不均匀、筒身直度不同、筒身圆度不同等各方面因素的影响，失稳形态都不一致。但是，整个试验过程中，所有易拉罐均未出现如同有限元特征值分析中所描述的纵向的波形。如果线性小挠度理论应用在薄壁圆筒的轴向失稳过程中是正确的，则试验现象与假设结果将出现矛盾。

表3所呈现的数据结果和表1的试验数据显示，试验临界载荷值与理论临界载荷值误差在5%以内，同时试验测得的各临界应力数据较为稳定，因此试验结果有效。由ANSYS有限元软件分析的结果来看，根据线性理论计算得到的的临界应力远远大于根据非线性理论计算得到的临界应力，且与理论值之间的误差过大。同时，非线性分析的结果与试验结果以及理论结果都十分契合，这就充分证明了薄壁圆筒的轴向受压到失稳的过程符合非线性理论，将线性小挠度理论应用于薄壁圆筒的轴向失稳是不正确的。

3.3 易拉罐作为试验试件的可行性

尽管各试验用易拉罐圆筒在失稳形态上并不一致，但是鉴于试验数据结果与理论值吻合，且其作为试验材料成本较低，取材方便，将易拉罐圆筒作为薄壁圆筒轴向外压试验的试验试件是可行的。而能否进一步推广至实验室甚至是工程领域，还需要多次试验来评价其可靠程度。

4 结论

通过析轴向外压试验和有限元分计算分别对易拉罐进行屈曲分析，发现对于薄壁圆筒的轴向失稳是不能采用线性小挠度理论进行分析而应该采用非线性前屈曲理论分析。工程设计标准上，如果采用线性理论，则临界值过大，易发生危险，必须采用非线性前屈曲理论[14]。在试验方法与分析方法上，对压力容器轴向失稳的过程给予了较为直接易懂的理解方式。试验设备简单、可操作性强，为学生自主创新和创造搭建了创新平台[15]，结论对于工程实际具有借鉴意义。

[1]陈盛秒.薄壁外压容器设计的图算法与解析公式法[J].石油化工设备,2009,38(1):37-41.

[2]刘鸿文,林建兴,曹曼玲.板壳理论[M].杭州:浙江大学出版社,1987.

[3]黄克智.板壳理论[M].北京:清华大学出版社,1987.

[4]聂君峰,李晓轩,张海泉.壳体容器跌落事故的相似试验设计与有限元分析[J].原子能科学技术,2012,46(10):1237-1242.

[5]李伟,陈孟诗,邹远文.多功能材料力学实验系统的设计[J].实验科学与技术,2007,7(5):29-31.

[6]戚坤.卡箍性能有限元分析与测力仪研制[D].湖北工业大学,2010.

[7]肖信.Origin 8.0实用教程:科技作图与数据分析[M].北京:中国电力出版社,2009.

[8]李建雄,谢永鹏,苗明川.全息干涉测铝板杨氏模量算法的讨论[A].全国高等学校物理基础课程教育学术研讨会[C]. 浙江,2007.

[9]高炳军,唐辉永,苏亮.“露露”易拉罐作为外压圆筒稳定性试验试件的可行性研究[J].河北工业大学成人教育学院学报,2008,23(1):53-56.

[10]张红信,管殿柱.有限元基础理论与ANSYS 11.0应用[M].北京:机械工业出版社,2009.

[11]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007.

[12]王志文,蔡仁良.化工容器设计3版[M].北京:化学工业出版社,2012.