离心通风器转子壁面油膜分布的数值研究

胡 慧，徐让书，邵长浩，张所刚

(沈阳航空航天大学航空航天工程学部(院)，沈阳 110136)

油滴与气流以混合两相流的形式存在于离心通风器内［1－2］。垂直向下和水平流动中颗粒的沉积速率随驰豫时间(无量纲数)的增加而增加［3］。对于小stokes数的颗粒，方形管内的沉积率大于圆管内的沉积率［4］。不考虑湍流弥散时，油滴基本全部跟随旋转气流的运动轨迹，撞击到壁面上的油滴所形成的油膜大多分布在气流经过的位置，而湍流脉动引起的颗粒弥散现象改变了油滴的“正常”运动轨迹，可以使油膜在壁面上的分布更加均匀，更接近实验结果［5］。除了离心力作用外，气流在壁面上的碰撞过程对提高分离效果也具有重要作用［6］。Farrall等［7－8］研究了轴承腔内空气、油滴颗粒和油膜行为的两相数值建模方法，其模型包含了重要的颗粒与油膜间的相互作用。当分散相油滴颗粒的含量较少时，可以采用针对于单个颗粒的动力学模型，只考虑连续相对分散相的作用［9－10］，忽略分散相对连续相流动的影响与动量贡献，颗粒相之间的相互作用与颗粒自身的脉动都不计入数值计算范畴［11－12］。由于离心通风器具有与轴承腔内的油/气两相流相似的流动特征，因此本文以离心通风器内空气与滑油颗粒组成的两相流为研究对象，应用计算流体力学(Computational Fluid Dynamics，CFD)方法［13－14］，分别计算通风孔偏心距e为5 mm、7 mm、9 mm时各壁面油膜厚度值，并分析了偏心通风孔对各壁面油膜厚度的影响。

1 数值计算

1.1 计算域与计算网格

如图1所示，为模拟离心通风器转子在实验腔内分离油气过程中的壁面油膜的分布，将整个计算域由转子壁面分割为:实验腔;旋转辐板腔;通风孔腔;空心旋转轴腔。通风器空心轴上的径向通风孔和辐板在周向上均布，即通风器流道结构具有以60°为周期的旋转周期性，所以实际计算过程中选取整体流动域的轴向1/6为计算域。

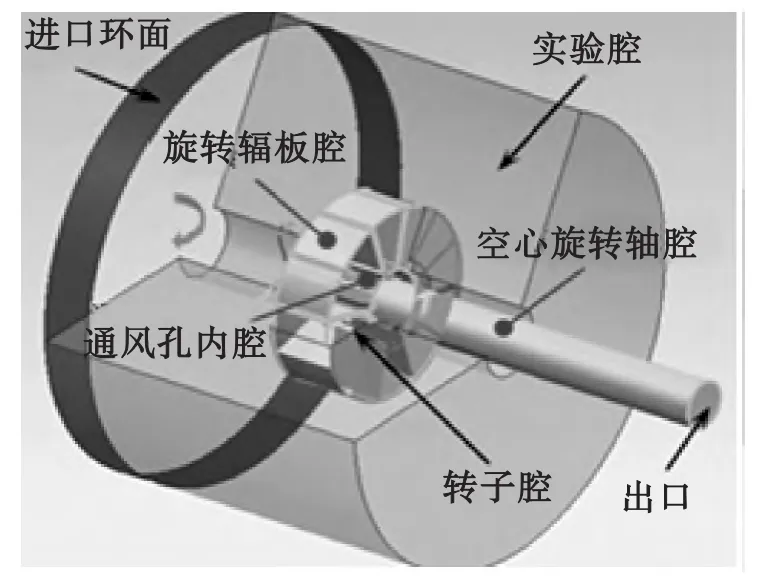
图1 整体计算域

工作时，来自轴承腔的滑油颗粒与空气一起流入通风器实验腔，在离心力的作用下，旋转轴带动辐板高速旋转，由于滑油颗粒的密度大，受到的离心力远大于空气，从而滑油颗粒被分离到壁面上形成一层油膜，通过回油孔回收，未被分离的油滴随空气从通风孔流经空心旋转轴，最后被排入大气。

良好的计算网格是快速获得精确收敛解的有效保障。由于离心通风器内部流道结构具有一定的复杂性，采用分块划分网格的方法将整个计算域分割为多个具有独立特征的几何体，然后以控制线网格的方式划分各块的网格。由于通风孔及其上下游的共面几何体特征不一致，所以局部网格采用四面体网格，四面体网格分布如图2所示，其余计算域均为六面体网格。为适应壁面处油膜与气流的两相流动的模拟，靠近壁面处的网格采用边界层处理，保证y+在合理范围内。

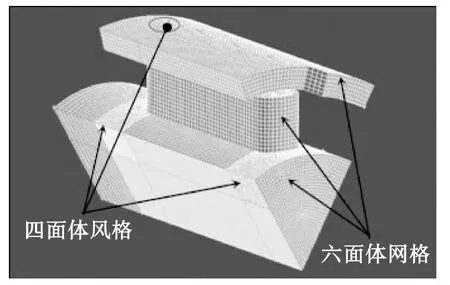
图2 通风孔及其上下游网格处理

1.2 边界条件及计算方法的定义

入口边界条件为质量流量入口，质量流率为总通风流量的1/6。湍流强度采用适用于管内充分发展流动的经验公式计算为5%，湍流粘性比给定为500，各壁面表面粗糙度给0.0002。采用DPM模型模拟颗粒的初始喷射条件，初始喷射以颗粒包文件的形式给定颗粒的初始位置、速度、温度、颗粒直径大小等。其中，颗粒的初始位置与速度均采用随机分布形式，颗粒直径大小的分布采用R分布，入口与出口的DPM边界条件均为逃逸(escape)类型。取标准大气压力(10.132 5 kPa)为参考压力，出口定义为压力出口，出口静压(表压力)为 Pg，cut=0 kPa。

采用雷诺应力方程模拟通风器内的气流流动，首先计算稳态下的连续相流场，然后以该流场做为初始化条件，计算非稳态下的颗粒颗粒轨迹追踪。采用标准壁面函数进行近壁处理，离散相的壁面边界用壁面液膜模型处理，模拟离心通风器内部油滴颗粒与壁面油膜碰撞后的各种情况。颗粒的轨迹追踪可以采用随机轨道模型［15］，这样就以可控时间步长的方式，模拟离心通风器稳态流场内颗粒的轨迹运行情况。亚松弛求解直至收敛，求解收敛的判断标准为残差小于10－3。

2 物理方程

2.1 颗粒的运动轨迹

颗粒运动轨迹方程通过对其受力积分获得:

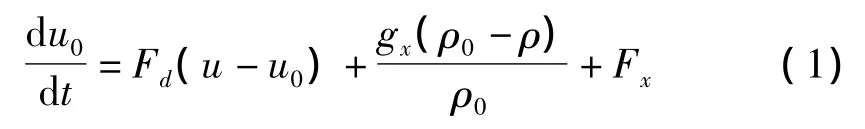
式中:u0为油滴速度，u为流体速度，ρ0为油滴密度，ρ为流体密度，Fd(u－u0)。为单位颗粒质量受到的空气阻力。油滴轨迹跟踪模型中提到的速度是流体的瞬时速度，积分颗粒轨迹方程就可以得出颗粒轨迹。

2.2 颗粒的Stokes数

颗粒在气流中的运动状态受颗粒的动量非平衡程度影响，主要受力分为自身惯性力和来自气流的力。动量非平衡程度可以按St数定来度量，其值为颗粒响应时间与系统响应时间之比:

式中，τd为颗粒响应时间(也称为松弛时间或弛豫时间)，代表颗粒与连续相动量非平衡松弛过程的快慢，在连续相速度为常数以及Stokes阻力条件下，颗粒相对于连续相的速度按指数规律衰减，经过时间τd后衰减为初始值的e－1，τs为系统响应时间，为系统特征长度Ls与特征速度Vs之比，即τs=。当St=1时，颗粒将紧密跟随连续相，主要受流体漩涡的影响，离心通风器内的滑油油滴颗粒直径为数十微米，典型情况下St数为0.01，当St=1时，颗粒的运动将独立于连续相，受自身惯性力的影响。

2.3 颗粒与壁面液膜相互作用

根据壁面温度T和碰撞能量E，油滴与壁面相互作用会发生如下图所示四种结果:粘附、散布、飞溅和反弹。

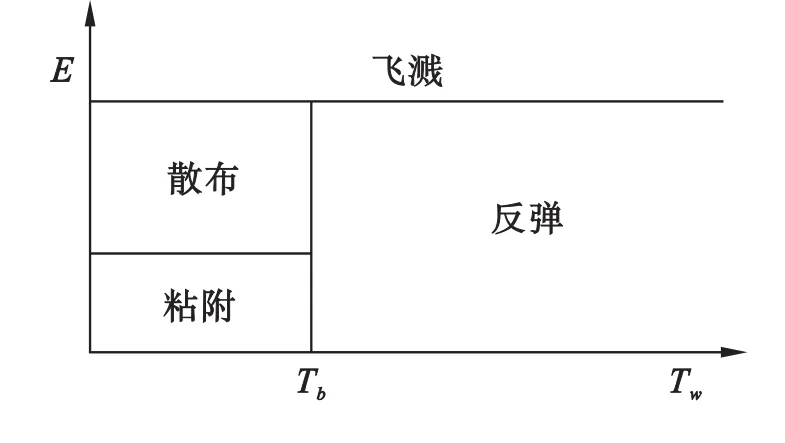
图3 液滴与壁面相互作用的结果

T＜Tb(油滴沸点温度)时，若E小于16，颗粒粘附于壁面。若E大于16时，颗粒散布于壁面，颗粒的初始方向和速度利用壁面射流模型确定。T＞Tb(油滴沸点温度)时，若E小于57.7，这时发生反弹，若E大于57.7则发生飞溅。碰撞能量关系式如下:

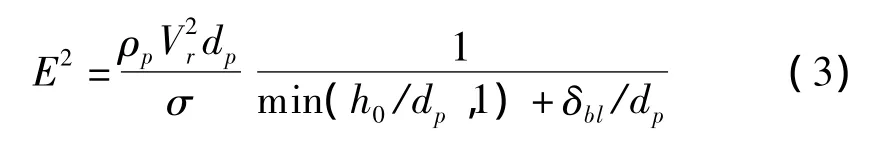
式中:Vr为油滴颗粒相对于壁面的速度，σ为油滴颗粒的表面张力，h0为初始的油膜厚度，δbl为壁面边界层厚度。

Vr为Rep的特征速度。

2.4 油膜分离准则

当油膜的边缘应力大于油膜对壁面的粘附力时，油膜就会从壁面分离。这些力很复杂并且屈居于局部壁面条件。对油膜的转角数量级分析表明液膜边缘应力与角度成正比。

2.5 壁面液膜上颗粒群的动量守恒方程

壁面液膜上颗粒群的动量守恒方程为:

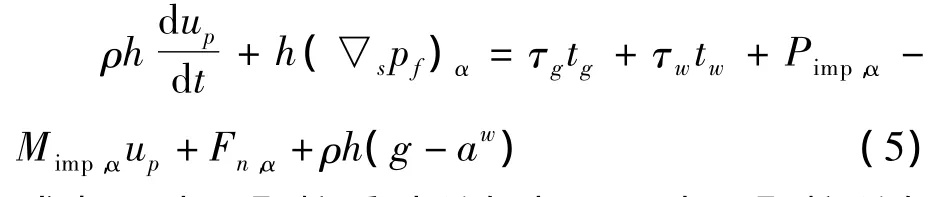
式中，α表示颗粒瞬时所在表面;h表示颗粒所在位置油膜的厚度;▽s是表面梯度;pf为油膜表面压力;τg表示空气流经液膜表面时的剪切应力大小;tg为空气与液膜表面相对运动方向的单位矢量;τw为壁面对液膜的剪切应力大小;tw为壁面与液膜相对运动方向的矢量大小;Pimp，α为液膜表面的撞击压力;－Mimp，αup为碰撞损失的动量;Fn，α壁面与液膜的粘附力;ρh(g－aw)为体积力项，需要说明的是尽管采用移动壁面时，可以看到在加速度的作用下油膜会很薄，但是体积力仍然是重要的。

3 CFD计算结果与分析

3.1 各腔室内流动状态分析

图4为CFD计算的离心通风器流道内各腔室的流动迹线图。从图中可以看出，离心通风器内流动较为复杂，流线弯曲特点明显，流动速度分布的跨度较大。

图4 各腔室流动迹线图(单位m/s)

辐板腔内流线弯曲和回折特点明显，可以看出油气混合气进入辐板腔内后，不是直接冲向下游，而是在整个辐板腔内形成一个较大的漩涡。此外，由于旋转辐板的高速旋转，使该区域的流体获得了很大的切向运动，因此辐板腔内的流体速度较高，在100 m/s左右。上述各因素，都使跟随气流一起运动的油滴颗粒的碰壁概率有很大提高。

由于通风孔形成了类似喉道的流动结构，使气流经过通风孔时损失掉一部分能量，速度减小到50 m/s左右。虽然流速减小增大了气流经过该区域的时间，但通风孔内的气流是沿着径向(即通风孔壁面的切向方向)，因此油滴颗粒在通风孔腔中的碰壁几率很低。

气流由径向的通风孔流到轴向的旋转空心轴腔会发生突然的的弯折，也会导致流速减小。但是，偏心通风孔使气流获得更大的切向速度，增大了气流中油滴颗粒的碰壁几率。

3.2 通风器内颗粒浓度分析

图5为CFD计算的离心通风器内的颗粒浓度分布情况。从图中可以看出，油滴的颗粒浓度主要分布在0至0.3(单位:kg/m3)范围内，分离的主要区域为实验腔。

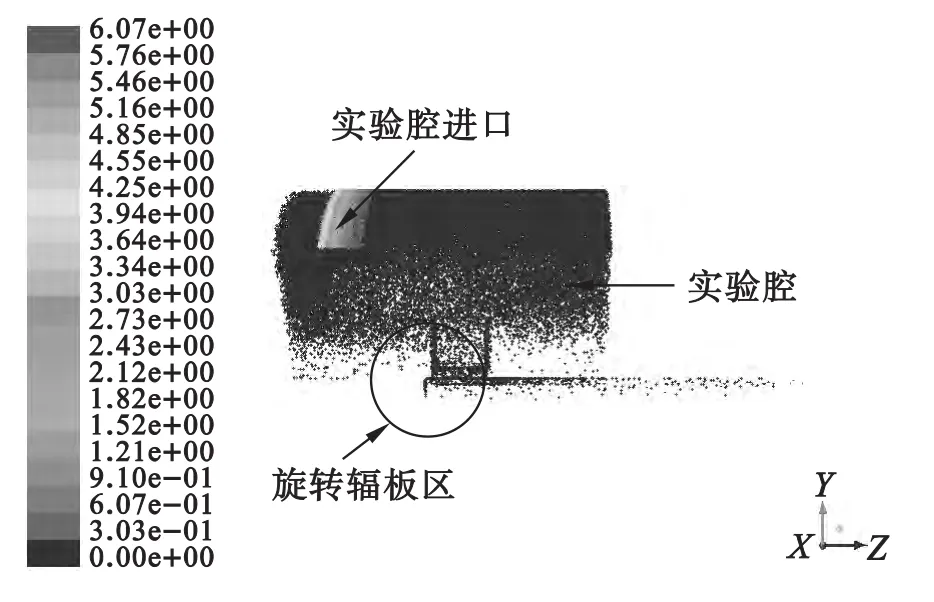
图5 离心通风器内的颗粒浓度分布

夹杂着滑油油滴的气流进入通风器试验器，首先冲向旋转辐板区，旋转的辐板使试验器腔内气体高速旋转产生离心力，使直径较大的颗粒被分离，加大了油滴碰到实验腔壁面形成油膜的几率，这样油膜在辐板侧壁面的厚度必然增加，而直径较小的颗粒随气流弥漫于通风器实验腔内。偏心通风孔的设计使进入空心轴腔内的气流与轴腔内螺旋气流的方向一致，使空心轴腔内的气流获得更大的离心加速度，更多的油滴颗粒向空心轴壁面迁移，形成更高的油膜厚度。由于通风管内的螺旋气流使油滴颗粒受到一定的离心力，所以在通风管中也存在分离，也会有油膜产生。

3.3 壁面捕获颗粒的能力

各壁面捕获颗粒的能力用每个腔室内颗粒的碰壁质量率统计，碰壁质量概率的物理定义为:腔室入口颗粒的质量流量采样值与出口颗粒的质量流量采样值之差除以腔室入口颗粒的质量流量采样值。各段壁面的碰壁率在图6中给出。

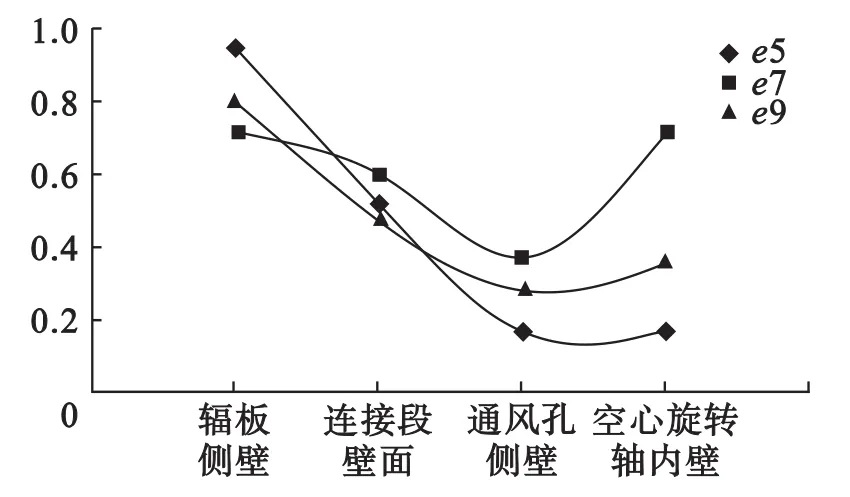
图6 各腔室的碰壁质量概率

从图6中可以看出，由于辐板腔内存在较大的流体漩涡，增大了油滴颗粒的碰壁几率，所以辐板侧壁对颗粒的捕获能力较高，一般在0.8左右。e=7 mm时，连接段壁面、通风孔侧壁和空心旋转轴内壁的颗粒捕获能力都高于其他两种情况下各壁面的碰壁质量概率。e=5 mm时，通风孔侧壁和空心旋转轴内壁的颗粒捕获能力很低。

3.4 壁面剪切应力分析

图7为辐板侧壁的剪切应力分布，可以看出高剪切应力出现在辐板偏左上侧，并以此为中心向边缘方向递减。辐板上边缘剪切应力偏高，大概为20～30 Pa，下边缘中间段存在高剪切应力，两侧剪切应力几乎为零。

图7 辐板侧壁的剪切应力分布

图8为通风孔内壁的剪切应力分布，可以看出通风孔的出口边缘处剪切应力随偏心距的增加而增大。高剪切应力主要分布在通风孔的入口后端和出口前端。当e为9 mm时，通风孔的出口前端剪切应力达到143 Pa，并且沿着出口边缘有一定的分布范围。入口后端壁面边缘的最大剪切应力约为100 Pa。

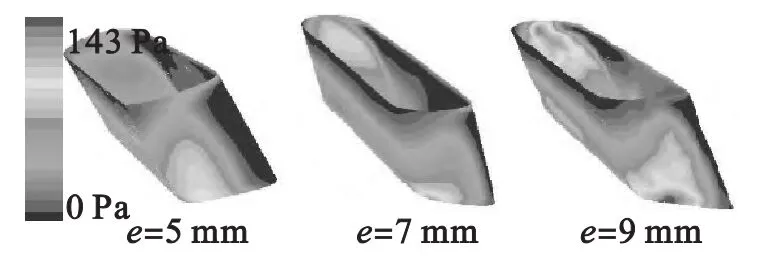
图8 通风孔内壁的剪切应力分布

图9为空心旋转轴内壁的剪切应力分布，越接近通风孔处的剪切应力越大，剪切应力主要分布在10～70 Pa之间。

图9 旋转空心轴内壁的剪切应力分布

3.5 壁面油膜厚度CFD计算结果

CFD计算的不同通风孔偏心距下各壁面的油膜厚度值如表1所示。从表中可以看出，辐板侧壁的油膜厚度随e的增加而增大。主要是因为通风孔偏心增大了气流阻力，使气流吹飞壁面边缘处油膜的动力减小。但是，偏心距增大使辐板上的剪切应力提高(如图7)，使油膜向辐板壁面边缘迁移的趋势增强。

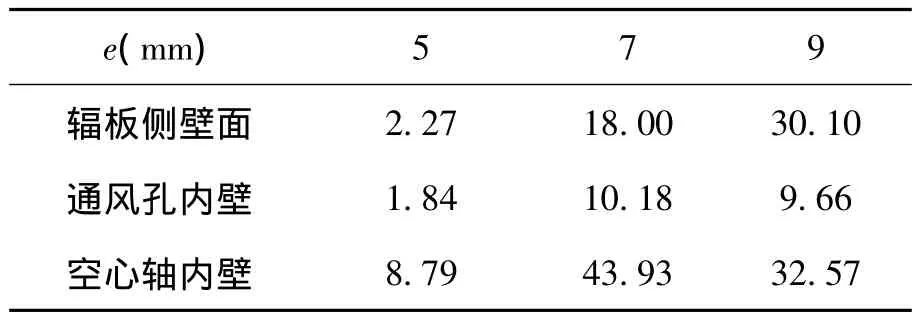
表1 各壁面油膜厚度计算值(单位10－10m)

通风孔内壁和旋转空心轴内壁的油膜厚度在e为7 mm时最大。相较于e为5 mm时各壁面的油膜厚度，e为7、9 mm时的油膜厚度要高出一个数量级。这是因为加大偏心距使通风孔壁面边缘处形成更高的剪切应力区(见图8)，驱动壁面油膜向上游运动，这一方向与气流运动方向相反，这样油膜在通风孔内壁面上厚度必然增加。偏心通风孔使进入空心轴腔内的气流与轴腔内螺旋气流的方向一致，加大了空心轴腔内气流的离心加速度。油滴颗粒向空心轴壁面迁移的几率增加，更多的油滴颗粒碰壁后，形成的油膜厚度自然要更高。但是通风孔偏心距的增大，使通风孔出口壁面边缘处应力增加，这样油膜被吹飞的几率更高。

4 结论

本文在旋转坐标系下应用DPM模型采用CFD方法计算离心通风器内的气液两相流动情况，并用壁面液膜模型模拟颗粒的碰壁机制。计算并分析了偏心通风孔对各壁面油膜厚度的影响，所得主要结论为:壁面油膜厚度受剪切应力的影响。增大通风孔偏心距使各壁面的剪切应力提高，增大了油膜向壁面边缘迁移的驱动力。辐板壁面的油膜厚度随通风孔偏心距的增加而加大。在e为7 mm时，通风孔内壁和空心轴内壁的油膜厚度出现最大值。

［1］航空发动机设计手册总编委会.航空发动机设计手册:传动及润滑系统:第12册［M］.北京:航空工业出版社，2002:507－508.

［2］马枚.航空发动机轴心通风系统的结构演变及分析［J］.燃气涡轮实验与研究，1994(4):23 －30.

［3］刘洪涛，张力.微细颗粒壁面沉寂的数值研究［J］.工程热物理学报，2010，31(3):431 －434.

［4］ Winkler C N，Rani S L，Vanka S P.A.Number Study of Particle Wall deposition in a Turbulent Square Duct Flow［J］.Power Technol，2006，170(1):12 －25.

［5］徐让书，宗庆贺，刘立博，等.湍流弥散对轴心通风器油气分离的影响［J］.航空发动机，2011，37(4):5－9.

［6］周华，夏南.油气分离器内气液两相流的数值模拟［J］.计算力学学报.2006，23(6)，767 －771.

［7］ Farrall M，Hibberd S，Simmons K.The effect of initial injection conditions on the oil droplet motion in a simplified bearing chamber［J］.Journal of Engineering for Gas Turbines and Power，2008，130(1):012501 －1－0125018.

［8］ Eastwick C N，Simmons K，Wang Y，et al.Study of aero-engine oil-air separators［J］.Proc.Journal of Power and Energy，2006:707 －717.

［9］ Gorse P，Busam S，Dullenkopf K.Influence of operating condition and geometry on the oil film thickness in aero-engine bearing chambers［J］.Proc.of ASME Turbo Expo 2004，Vienna，Austria，June 14 －17，2004.

［10］ Said Elghobashi.An updated classification map of particle-laden turbulent flows［C］.Proceedings of an IUTAM Symposium held at Argonne National Laboratory，October 4 －7，2004.

［11］张楠，刘振侠，吕亚国，等.航空发动机滑油系统叶轮式通风器数值计算研究［J］.科学技术与工程，2011，10(15):130 －133.

［12］冯健美，畅云峰，张勇，等.喷油压缩机卧式油气分离器特性的数值模拟及实验研究［J］.西安交通大学学报，2008，42(5):561 －577.

［13］ A Glahn，S Busam，M F Blair，et al.Droplet generation by disintegration of oil films at the rim of a rotating disk［J］.Journal of Engineering for Gas Turbines and Power，2002，124:117 －124.

［14］ A Glahn，M F Blair，K L llard，et al.Disintegration of oil jets emerging from axial passages at the face of a rotating cylinder［J］.Journal of Engineering for Gas Turbines and Power，2003(125):1003 －1110.

［15］孙秀君，孙海鸥，姜任秋.油气分离器内有底轨迹的数值模拟［J］.应用科技，2006，33(10):69 －72.