基于Haar小波变换的码元速率估计

61251部队 安佰强

吉林大学计算机科学与技术学院 61251部队 郑 伟

解放军电子工程学院 罗高健

61251部队 陈晓辉

码元速率是数字通信中最重要的参数之一，对码元速率的准确估计在通信对抗中有着重要的意义，它是实施无线电通信干扰时选择干扰样式和干扰参数的重要依据，也是进行通信信号盲识别和盲解调的重要前提。本文提出了一种在没有任何先验知识的条件下，采用Haar小波对中频信号进行码元速率估计的算法。这种算法可以在较低的信噪比下对ASK、PSK和QAM调制信号进行有效的码元速率估计，并且容易在FPGA上实现。

1.基本原理

假设经过前端处理后的中频信号为x(t)，载频为fc，以采样频率fs对x(t)进行采样，得到离散信号x(k)，设其数学模型为：

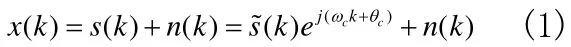
这里s(k)是调制信号，n(k)是高斯白噪声， ωc=2πfc/fs是信号的数字频率，θc为载波的初始相位。(k) =Akejφk代表码元的幅度和相位信息，在同一个码元内，(k)的值不变。根据幅度Ak和相位φk取值范围的不同，(k)可以分别表示MASK、MPSK和MQAM信号。

小波变换具有在时间和频率上突出信号的局部特性的能力，因此可以利用小波变换提取信号码元间的跳变信息。离散小波变换的公式为：

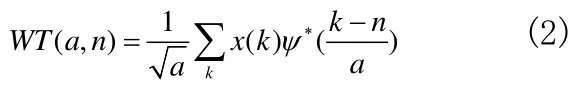
其中，a是尺度参数，n是时间平移参数，*表示复共轭，ψ是小波函数，本文选取离散Haar小波函数，并乘以一个与信号有关的系数x(n)。Haar小波函数为：

增加系数的Haar小波函数为：

式中尺度参数a取偶数。在不考虑噪声的情况下，对信号s(k)进行小波变换：

(a,n)的突变特性与尺度参数a的选择有着密切的关系，一般来说，小尺度下的小波变换能精确刻画信号的边缘信息，但受噪声影响较大，不利于码元速率的精确估计；大尺度下的小波变换对噪声有较好的平抑作用，但容易淹没真实局部极值，不能正确反映信号的局部特征。文献[7][8]研究了如何选择最优尺度和如何进行多尺度小波变换，利用他们提出的方法，可以大幅提高码元速率估计的准确性。为了便于分析，本文只讨论单一尺度的小波变换，并假设尺度参数小于一个码元周期，此时（5）式会出现两种情况：

1）在尺度参数范围内无码元变化，即当 -a/2 ≤k≤a/2- 1时，(k) =Aejφ，此时有：

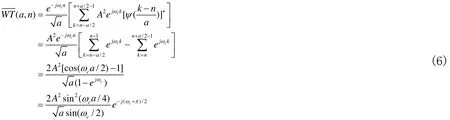
2）在尺度参数范围内有码元变化，即存在i满足 -a/2 ＜i≤a/2- 1，当 -a/2≤k＜i时，有(k) =A0ejφ0，当i≤k≤a/2- 1时，有(k) =A1ejφ1。为方便计算，不妨设i=n，此时计算的结果对分析小波变换的突变特性无太大影响。此时有：

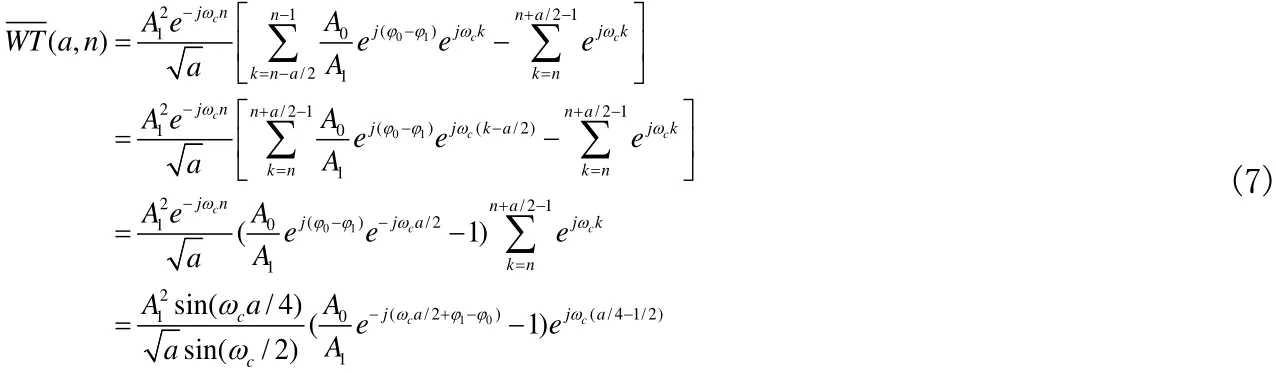
设PWT为的相位，则：

由（6）和（7）式可以看出，当无码元变化时，PWT为常数 - (ωc+ π)/2，当码元发生变化时（无论是相位变化还是幅度变化），都会使PWT产生突变，因此，PWT具有与码元相同的周期性。

在实际应用中，由于信号的码元不一定连续变化，可能会出现连续相同的码元，因此直接从PWT中获得码元周期信息比较困难。可以先对PWT做FFT变换，从频谱上估计码元速率，具体方法见下节内容。

2.算法仿真

用MATLAB工具对本文提出的算法进行仿真，以128QAM调制信号为例。产生载频fc= 10KHz，采样率fs= 100KHz，码元速率fd=4KHz的128QAM数字通信信号，噪声为高斯白噪声，SNR=5dB，取N= 1024点计算小波变换（尺度参数为2）。

MATLAB产生的128QAM信号如图1所示。

图1 128QAM信号（I路和Q路）

利用式（5）获得信号的小波变换，并计算其相位PWT，如图2所示。

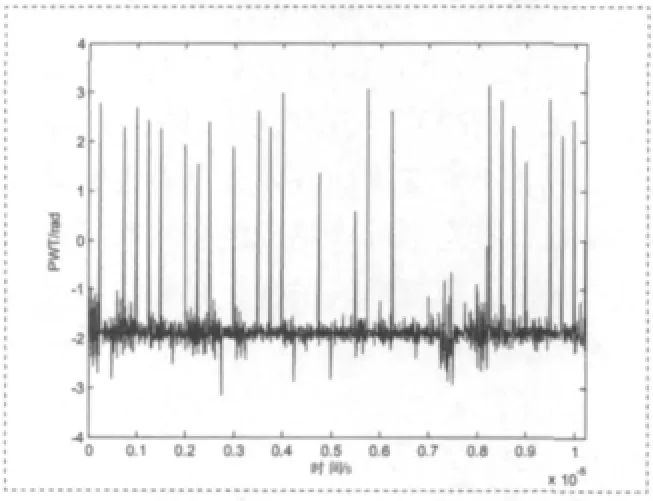
图2 128QAM信号的PWT

对相位PWT做FFT变换，获得相位的频谱FWT。未经处理的频谱具有较大的零频。去掉零频，并设置门限β，将低于β的频点滤除。β的取值可根据频谱的最大值max(FWT)确定（不含零频的最大值），在此设 β= 0.8max(FWT)。未经过处理的FWT和经过处理的FWT见图3。

图3 128QAM信号PWT的频谱

由图3可以看出，第一个谱峰对应的频率即为码元速率。也可以先计算出各谱峰间的距离，取其平均值来估计码元速率，以提高估计的精度。设谱峰的平均间距为ΔN，则码元速率可以表示为：

码元速率的估计精度Δf与频谱的频率分辨率相同，即为 Δf=fs/N。

3.仿真结果

为了分析不同噪声条件和调制方式对码元速率估计性能的影响，我们在不同信噪比下，分别对4ASK、8ASK、BPSK、QPSK、64QAM和128QAM六种调制信号进行1000次码元速率估计。设估计误差在±Δf内为准确估计，则当尺度参数a=2时，码元速率估计的准确率如图4所示。这六种通信信号的参数为载频fc= 10KHz，采样率fs= 100KHz，码元速率fd=4KHz，码元个数N=100。

图4 码元速率估计的准确率

从仿真结果可以看出，在信噪比不低于4dB时，此算法对码元速率估计的准确率可以达到95%以上。值得指出的是，64QAM和128QAM的估计效果较好，其原因是QAM调制信号在码元之间不仅有相位突变，同时还有幅度突变，包含更多的码元突变信息。

4.结论

本文提出的利用Haar小波变换估计中频信号码元速率的算法，充分利用了码元变化时的幅度突变和相位突变信息，可以在较低的信噪比下正确获取MASK、MPSK和MQAM调制信号的码元速率。在低尺度参数下，该算法可以较容易的在FPGA上实现，具有一定的实用价值。

[1] 邓振淼,刘渝.基于多尺度Haar小波变换的MPSK信号码速率盲估计[J].系统工程与电子技术,2008,30(1):36-40.

[2] 许小东,路友荣,戴旭初,徐佩霞.一种基于最优尺度小波变换的符号率估计算法[J].中国科学技术大学学报,2008,38(10):1147-1152.

[3] 秦永,万国金,谢芳娟.基于小波变换的MPSK信号符号率估计方法[J].通信技术,2009,42(1):81-83.

[4] 冯旭哲,杨俊,罗飞路.基于小波变换的通信信号码元速率估计[J].系统仿真学报,2008,20(5):1259-1261.

[5] 张晓勇,罗来源,罗武忠.一种基于瞬时幅度的PSK信号符号速率估计方法[J].信号处理,2008,24(2):316-319.