X射线衍射方法分析粗晶铁硅合金的残余应力
2014-09-27姜传海
万 鑫,詹 科,姜传海
(上海交通大学材料科学与工程学院,上海 200240)
0 引言
残余应力是材料在机加工或合金化过程中产生的平衡于材料内部的应力。实践证明,金属材料中残余应力的大小和分布对机械构件的静态强度、疲劳强度、耐腐蚀性和构件的尺寸稳定性等都有直接的影响,同时对检查焊接、表面强化处理(喷丸、渗氮、渗碳等)和热处理等工艺效果,以及控制磨削等机械加工的表面质量都具有实际意义。目前,有多种方法可以用来测材料的残余应力,如机械拉伸法、小孔松弛法、光弹性法、中子衍射法、X射线衍射法等。其中,X射线衍射法因具有无损、快速、精确等诸多优点,已被广泛应用[1]。
残余应力按其作用范围可分为宏观残余应力(第Ⅰ类残余应力)和微观残余应力(第Ⅱ类和第Ⅲ类残余应力)。宏观残余应力是指在晶体材料宏观尺度范围内保持平衡的一种内应力,微观残余应力则是指平衡晶体材料内部几个晶粒之间甚至更小范围内的残余应力。实际上,在发生塑性变形的金属中,这两类应力通常是共存的。
目前用X射线法测大块单晶或粗晶材料并不多见。由于单晶材料内部各向异性,对其残余应力测量有较多难点,例如晶体取向的确定、衍射峰位置的确定和衍射仪的校正等,因而单晶材料残余应力测定结果的可靠性较差[2];另外,单晶和粗晶材料残余应力的测量往往耗时过长。鉴于单晶和粗晶材料的使用日益广泛,Imura等提出了测量单晶材料残余应力的改进方法[3],在此方法中,先设法求得弹性应变的张量,然后再根据胡克定律推导出全部的应力张量。作者尝试利用Imura方法测量了粗晶铁硅合金的残余应力,并且对测量结果进行分析和可靠性讨论。
1 试样制备与试验方法
1.1 试样制备
试验材料为Fe-1%Si合金,将其切割加工成如图1所示试样,经过再结晶处理(600℃保温3 h)后获得了较大尺寸的晶粒(约10 mm),采用Imura方法测试样的残余应力,试样的点1和点2为XRD测量点。计算应力需要用到该合金的弹性力学常量:C11=232 GPa,C12=135 GPa 和 C44=116 GPa[4]。
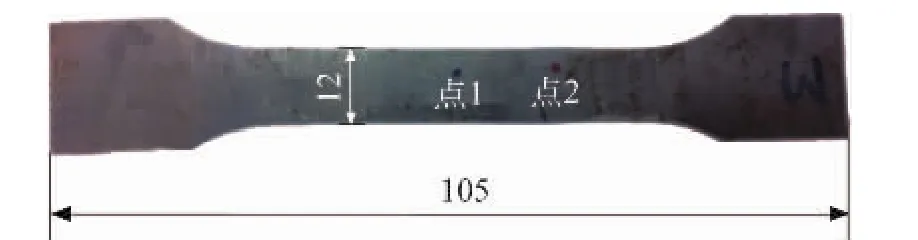
图1 试样的形状与尺寸Fig.1 Shape and dimension of sam p le
Fe-1%Si合金具有较大的晶粒尺寸,传统的多晶材料残余应力测量方法不再适用。它的微观结构示意如2所示。可见,当X射线照射试样表面时,只有单个晶粒发生衍射,因此可以利用单晶残余应力的分析方法来分析此类材料。
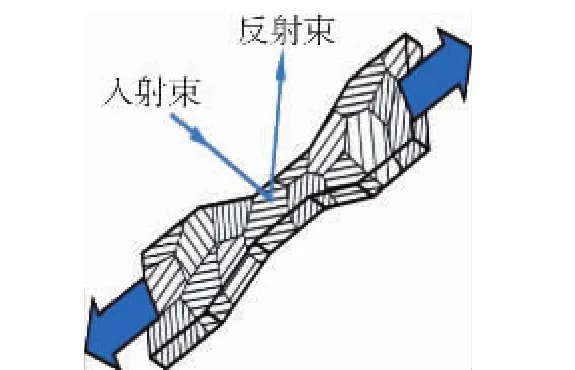
图2 试样的微观结构示意Fig.2 Diagram of them icrostructure of samp le
1.2 测试原理
在Imura等提出的方法中,先设法求得弹性应变的张量,然后再根据胡克定律推导出全部的应力张量。其中,弹性应变张量(应变矩阵)由6个互相独立的因子组成,即3个对角线应变(ε11,ε22,ε33)和3 个非对角线应变(ε12,ε23,ε13)。因此,应变 的张量可以写成:
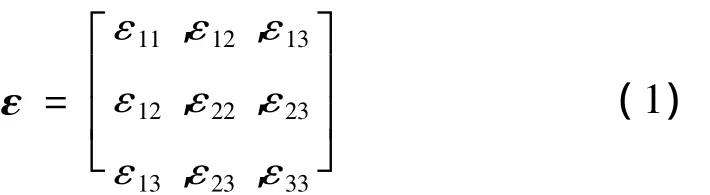
由式(1)可以看出,若要计算出应变张量,必须至少获得6个互相独立的测量数据点。通过测量材料变形前后衍射峰(θ)的相对位移可以实现应变张量的测量,晶格的应变与衍射角之间满足布拉格定律。
下面将仔细阐述这种方法计算残余应力的原理。从图3可见,单晶材料发生变形后,衍射峰的位置也随之变化。图中d(hkl)和d0(hkl)分别为变形前后的(hkl)晶面间距;θ为偏移后的入射角;θ0为原始入射角。
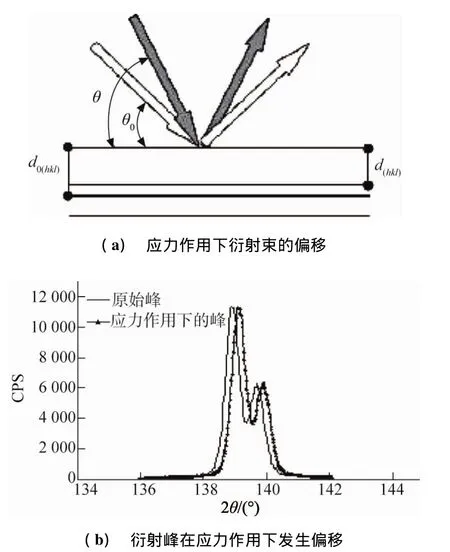
图3 材料变形所引起的衍射峰的移动[5]Fig.3 Displacement of diffracted peak induced by deformation ofmaterial:(a)movement of diffracted beam s under stress and(b)movement of diffracted peak under stress
为了应用这种方法,需要通过测量独立晶面的晶面间距来求得对应应变张量的独立因子至少6个。对于应变ε(hkl),发生衍射的晶面(hkl)之间的距离在晶体坐标系中可以写成:
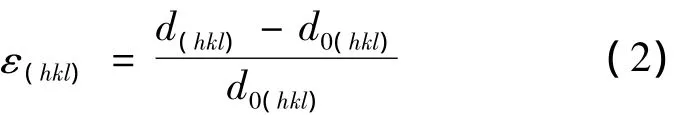
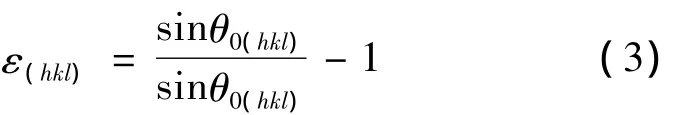
通过体坐标系和试样坐标系的转换矩阵n(hkl),可以将晶格应变转换为弹性应变,即:
根据Bragg关系可以将式(2)改写成:
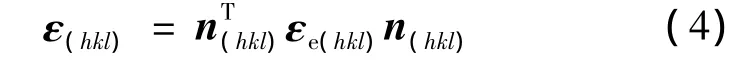

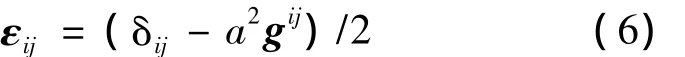
度量张量的计算是一个求解线性方程组的问题,可以通过以下的公式进行推导。式(7)可以简写成:
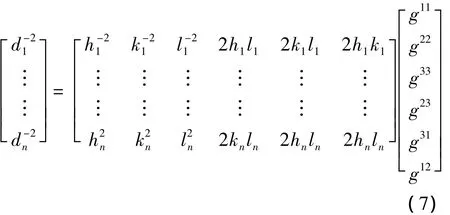

由式(8)可看出,为了求解线性方程组,至少要有6个相互独立的方程。因此,在使用此方法过程中至少要求得6个晶面以上的衍射角位置。根据式(8)和矩阵变换,度量张量G*可以写成:
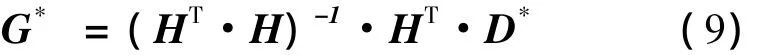
向量D*可以通过每组衍射晶面的衍射角和布拉格定律求得,H矩阵是由测量结果中各晶面的晶面指数决定的。因此,通过至少6个晶面的测量数据便可以求得度量张量gij。再结合式(6),便可以计算出晶体坐标系(Ac)中的应变张量。则可以通过材料特性计算出,再结合广义胡克定律便可以计算出晶粒坐标系中的应变张量。
晶体坐标系Ac和试样坐标系Ap的过渡矩阵M可以写成:
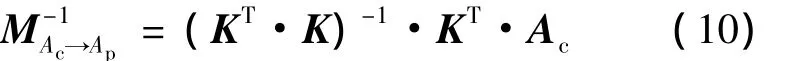
式 中:K = [k1,k2,k3,……,kn]T, 且 kn=(cosψn,sinψn,cosψn);Ac= [Ac1,Ac2,Ac3,……,Acn]T,Acn为晶粒坐标系中衍射晶面指数,即:Acn=(hn,kn,ln)。
接着,可以通过对M矩阵奇异值分解,找到旋转矩阵R,通过旋转矩阵便可将求得的应变和应力张量转换到试样坐标系中。即:
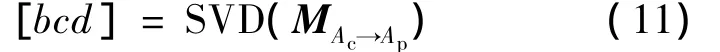
式中:b,c,d为奇异值分解结果的三部分。
旋转矩阵R可以写成:

最终,可以通过旋转矩阵R求得试样坐标系中的应力和应变的张量。其结果如下:
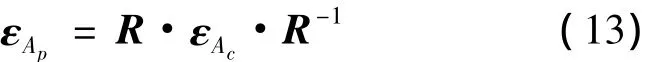
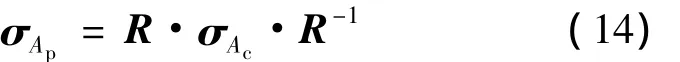
1.3 试验方法
使用SEIFERT XRD3000PTS型X射线衍射仪进行应力测试,X射线波长λ为0.229 09 nm,衍射位置由参数Ψ,φ确定,Ψ(绕x轴旋转方向)为试样法线和衍射面法线之间的角度,φ(绕y轴旋转方向)可以认为是测量位置绕试样法线的旋转角度,如图4所示。试验中,将Ψ的扫描范围设置为0°~70°,φ的扫描范围设置为0°~360°。铁在无应力状态下(211)面的衍射角2θ为156°。因此可以将初次扫描的衍射角设为156°,由于试样中存在应力,实际的衍射角度应该在这个角度附近。
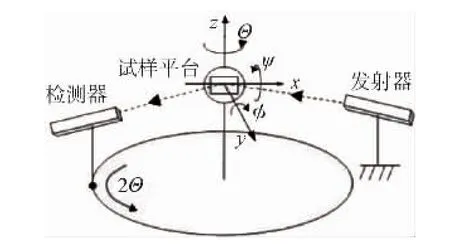
图4 SEIFERT XRD3000PTS衍射仪和角度示意[5]Fig.4 Diffractometer SEIFERT XRD3000PTS and schema of angles
衍射试验的步骤:初步扫描确定衍射晶面的位置,Ψ和φ的扫描步长为2°,2θ的扫描步长设为0.05°;在得到初步的衍射面位置和衍射角度后,根据这些角度重新设置参数,然后再将Ψ和φ的扫描步长调整为1°,2θ的扫描步长调整为0.02°,开始第二次试验;从第二次试验中可以得到更为精确的衍射面位置和衍射角度,再重新修改原始参数开始第三次扫描,并将Ψ和φ的扫描步长调整为0.5°,2θ的扫描步长调整为0.01°;同样,得到第三次试验结果后,继续修改原始参数设置,开始第四次试验,并将Ψ和φ的扫描步长调整为0.25°,2θ的扫描步长调整为0.01°。经过以上四步后,可以得到较为精确的衍射面位置和衍射角大小,保证了试验的精度。
2 试验结果与讨论
2.1 晶面指数和衍射峰位置的确定
在图5中可以看到共有7处衍射峰,与立方晶系(0 0 1)方向的标准投影图对比便可获得衍射晶面的晶面指数。
衍射晶面的位置确定后,再通过设定Ψ和φ来定位来这些晶面所对应的衍射角。在试验中可能会出现两个相邻的峰值,如图6所示,此时应选取强度最高的那组,这是由于使用的X射线中可能包含了Kα1和Kα2两种波长相似的射线。出现这种情况时,需要利用软件自带的Pseudo-Voigt函数对分峰进行处理,从而确定衍射峰的位置。
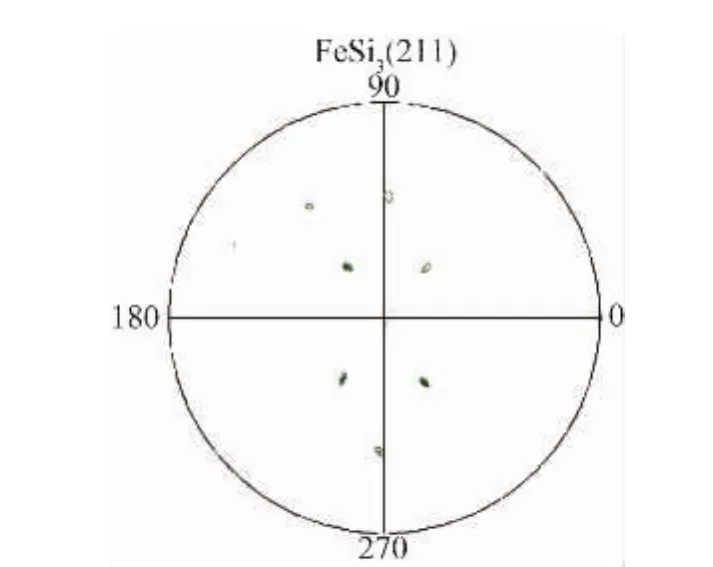
图5 {211}晶面族的位置Fig.5 Positions of{211}crystal planes fam ily
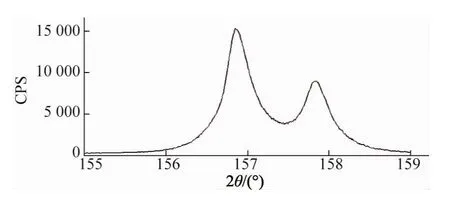
图 6 (2-11)面的衍射峰Fig.6 Diffraction peak of crystal plane(2-11)
衍射峰值处即为对应晶面的衍射角度,在得到了精确的衍射角度后,便可利用Imura方法来计算残余应力。由上可知,衍射角的精度直接影响了应力测试的准确度,而Ψ和φ的精度则可以反映出衍射角的精度。试验中,通过设定不同的扫描步长来保证准确找出衍射峰,越小的步长测出的结果越准确。此外,为了保证每次试验的准确性,先用铁粉做成的标准试样进行测试来调试机器参数,以减少试验的系统误差。
2.2 应力计算与结果分析
对铁硅试样进行了不同程度的拉伸,变形量分别为0%,2%,5%和10%,并且每次拉伸后在点1和点2位置进行应力测量,结果见表1。
从表1中可以看出,未发生变形时点1和点2应力张量的各个分量的绝对值都比较小,其中绝对值最大的仅为9 MPa,这是由试验中测量的不确定度造成的,主要体现在Ψ和φ的精度上。而σ33的值均接近于零,基本上符合初始状态中应力张量的理论值,验证了此方法是有效的,可以用来分析此类材料的残余应力。

表1 不同变形量铁硅合金试样上1点和2点处的残余应力张量各分量Tab.1 Components of Residual stress tensor at the point 1 and 2 on the Fe-Sialloy sample in different deformation degrees MPa
从表1还可知,拉伸变形后,相较于初始状态,两个点的应力都有明显增大,这是由于材料内部结构的各向异性使其在塑性变形后出现了残余应力;σ11增大最为明显,这是因为它的方向与拉伸方向一致,所以在这个方向上应力的增幅也最大;同时,横向的拉伸并不会在试样表面法向上造成应力,因此这几组测量结果中的σ33也都接近于0。由于每次都是在卸载外力之后对试样进行静态的应力测量,所以测得的各个应力分量均不显著。可见,以上这些试验结果都与理论预期相符。
从图7可以看出,随着变形量的增加,σ11也随之增大,而且总为正值。这是因为两个被分析的晶体有着相似的晶体学取向,它们都阻碍了塑性变形的滑移,即这两个晶体的取向因子(Schmid因子)较低,当试样被拉伸时,这两个晶粒内部很难发生塑性变形,从而导致宏观应力 σ11随之增大;拉伸结束后,便在这两个晶粒中残留了较为明显的应力,与周围晶粒对它们的压应力相平衡。
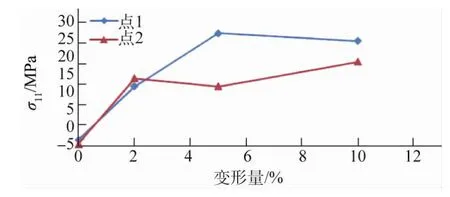
图7 铁硅合金试样上点1和点2处σ11随拉伸变形量的变化Fig.7 Variation of the stress σ11 with deformation degree at the point 1 and 2 on the Fe-Si alloy samp le
对于1点来说,随着拉伸变形量的增加,各个衍射晶面的半高宽度(FWHM)也随之增大,即衍射峰变宽,如图8所示。这是因为在单晶或者粗晶体中,参加衍射的晶面很少,即使很少量的位错和空位,也会对衍射面的峰位移产生比较大的影响。拉伸产生的塑性变形往往会伴随着位错的出现,较密集的位错就会导致衍射峰有变宽的趋势。因此,衍射峰的宽度在一定程度上反映了材料的应力水平和塑性变形程度,进而也可以反映材料中的位错密度等。
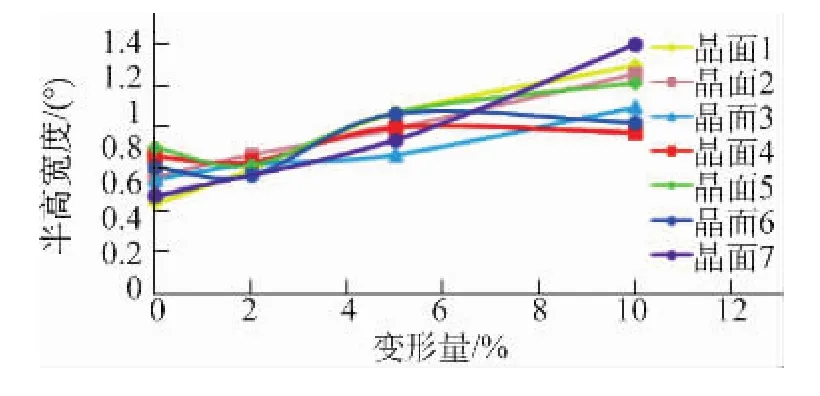
图8 各晶面半高宽度随着变形量的变化Fig.8 Variation of the FWHMwith deformation degree for different planes
然而,由于试验存在误差,造成了结果的小幅波动。试验中出现误差的主要原因有两点。其一为测量结果中的晶面数过少,由于仪器的限制,只找到了7~8组衍射峰较为明显的晶面,因此以上这些数据,全部是通过7组衍射晶面算出的,根据数学理论可知,参与计算的衍射晶面越多,计算的结果也就越精确。有研究表明,如果测出的晶面个数为18个时,残余应力的计算结果基本稳定[6]。其二为试验精度的设定,Ψ 和 φ 的精度为0.25°,2θ的精度为0.01°,如果减小上述两者的精度再次进行扫描,所得结果的精度就会更高,但是过小精度会造成测量时间大大增加,从而增大试验成本。按照本试验中的精度对试样完成一次扫描用时约为8 h。
3 结论
(1)运用了X射线衍射法测单晶材料残余应力的方法(Imura方法),成功地测得了粗晶材料铁硅合金的残余应力,测试结果与理论预期相符。
(2)采用Imura方法进行测试时至少要找到6个衍射晶面才可以计算残余应力张量,而且晶面数越多,计算结果越准确;晶面位置参数(Φ,Ψ)及衍射角精度2θ都会对试验结果产生影响,当晶面位置参数精度为0.25°、衍射角精度为 0.01°时,计算的应力状态基本符合试样拉伸后应力状态的理论值。若要得到更为接近于真实的应力分布状态,还需要找到更多的衍射面或采用其它改进方法。
(3)随着拉伸变形量的增加,各个衍射晶面的半高宽随之增大,即衍射峰变宽;这是因为拉伸产生的塑性变形往往会伴随着密集位错出现,较密集的位错会导致衍射峰有变宽的趋势。
[1]姜传海,杨传铮.材料X射线衍射与散射分析[M].北京:高等教育出版社,2010:213-220.
[2]陈艳华,须庆,姜传海,等.单晶材料X射线应力测定原理与方法[J].理化检验-物理分册,2012,48(3):144-147.
[3]IMURA T,WEISSMANN S,SLADE J J.A study of age-hardening of Al-3.85%Cu by the divergent X-ray beam method[J].Acta Crystallographica,1962,15(8):786-793.
[4]SAKATA K,DANIELD,JONASJJ.Estimation of8th,10th and 12th order ODF coefficients from elastic properties in cold rolled steel sheets by adjustment of single crystal[J].Textures and Microstructures,1990,12:175-185.
[5]HUANG WJ.Contribution à l'analyse par diffractomètre X des déformations et des contraintes à l’échelle des grains[D].Paris:Ecole Nationale Superieure d'Arts etMetiers(ENSAM),2007:18-52.
[6]鞠明,黄坚,吴毅雄.X射线衍射法测AM1镍基单晶合金的残余应力[J].机械工程材料,2013,37(3):99-103.
