Crowbar阻值对双馈感应发电机低电压穿越特性的影响

栗 然,王 倩,卢 云,刘会兰,祝晋尧

（华北电力大学 新能源电力系统国家重点实验室,河北 保定 071003）

0 引言

风电场对电网安全稳定的影响已成为风电发展的重要课题之一。如果大规模风电机组从电网解列，就不能支撑电网电压，进而导致连锁反应，对电网的稳定运行造成严重影响。因此各国电网的风电并网规范相继提出了低电压穿越LVRT（Low Voltage Ride Through）的要求，即要求风机在一定程度的电网电压跌落下维持可靠并网运行一定时间，从而为电网提供有功和无功支持，以利于电网电压的快速恢复和电网的安全稳定运行[1-3]。

双馈感应发电机DFIG（Doubly Fed Induction Generator）是目前主流风电机型之一，由于其变换器容量较小，对电网电压跌落造成的暂态过电流冲击尤为敏感，需要采取可靠的保护措施，防止变换器中功率器件损坏[4-6]。从研究方向上看，对于双馈感应风力发电系统动态特性及其低电压穿越能力的研究主要集中于3个方面：①DFIG控制策略的分析和改进[7-8]；② DFIG 硬件电路的改进[9-10]；③ 在风电场出口加装动态无功补偿装置、DVR、TCSC或串联电阻等[11]。通过改进DFIG控制策略提高低电压穿越能力只适用于并网点电压跌落不是很严重的情况；改进DFIG硬件电路最常见的措施是添加撬棒电路，即 Crowbar。文献[12-14]指出，Crowbar阻值的选取对低电压穿越影响较大，选取合适的Crowbar阻值有利于DFIG实现低电压穿越。目前，对Crowbar保护下的DFIG动态特性的研究主要集中在Crowbar阻值的选取及其与DFIG暂态电压、电流的关系上，而对Crowbar阻值与定转子暂态磁链和暂态电流衰减时间常数的数学关系方面的研究则并不深入。对电压跌落时DFIG电磁转矩波动的抑制措施也少有文献研究。

本文研究双馈感应风力发电系统低电压穿越时的Crowbar保护技术，针对DFIG机端发生三相对称短路机端电压跌落至零的情况，首先数学分析Crowbar阻值对DFIG运行特性、电磁转矩和转子转速的影响；然后在MATLAB/Simulink平台上搭建模型，通过设定不同电压跌落程度、不同Crowbar阻值验证理论分析的正确性；最后通过在Crowbar回路中串联附加电感缓和电压跌落发生瞬间DFIG电磁转矩的波动。三相短路故障发生在远离机端的电网导致机端电压部分跌落时，其对暂态直流磁链、电磁转矩和转子转速的影响规律相似，只是此时机端电压不再为零，本文不再单独分析。

1 Crowbar阻值对低电压穿越特性的影响

1.1 Crowbar阻值对DFIG运行特性的影响

1.1.1 理论分析

列写空间静止坐标系下DFIG的发电机矢量方程如式（1）所示[14]。

由式（1）可推得：

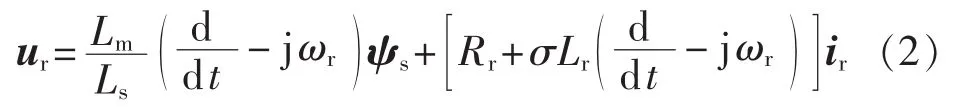
其中，u、i、R、L、ψ、ω 分别为电压、电流、电阻、电感、磁链和角频率；下标s和r分别表示定子和转子侧各变量。

以发电机出口发生三相短路故障为例，故障后Crowbar立即投入短接转子，突然发生的短路故障使定子绕组和转子绕组中分别感应产生相对定子和转子静止的暂态直流磁链，将其分别定义为：

其中，ψssn和ψrrm分别为定子和转子暂态直流磁链的空间矢量；ψs0和ψr0分别为定、转子直流磁链的幅值；α和α′为初始相位；上标s和r分别表示相对定子和转子静止的空间坐标系下各变量的表达式；下标n和m分别表示定子和转子直流磁链作用下产生的各电气量。将定子和转子暂态直流磁链的特性分开考察，首先假定故障后定子和转子直流磁链恒定不变。

设Rcrowbar为Crowbar电阻阻值，则在出口三相短路且Crowbar投入的情况下应满足：

将式（3）中第 1 式和式（4）中第 2 式代入式（2）并整理得：

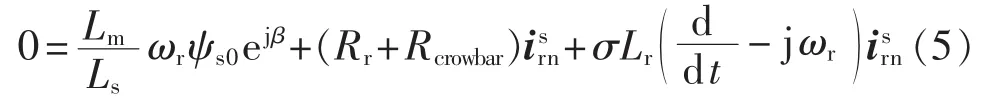
其中，β=α-90°。

将式（5）变换到转子坐标系下可得：

将式（6）整理成相量的形式如式（7）所示：

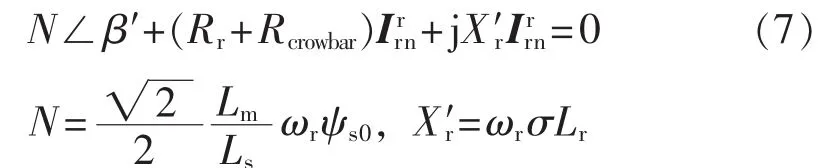
则：

不计励磁支路电流，近似认为：

将式（8）代入式（9）并变换到定子坐标系下可得：

β′经坐标变换后变为 β″。 由式（8）和式（10）可以得到恒定子直流磁链作用下系统的有功损耗为：

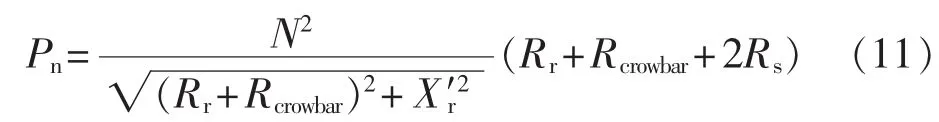
对式（11）进行数学处理可知，Pn取最大值时应满足：

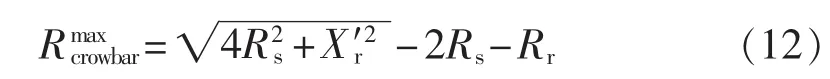
此时有功损耗最大，与之对应的定子直流磁链的衰减速度也最高。

以上是对定子直流磁链影响的讨论，接下来对转子直流磁链的影响进行分析。将式（3）中第2式变换到定子坐标系下：

其中，α″为转子直流磁链变换到定子坐标系下的初始相位。

仿照式（2），由式（1）可得：

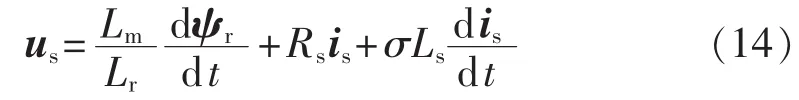
将式（4）中第 1 式和式（13）代入式（14）可得：

其中，θ=α″+90°。

将式（15）变换成相量表达式后整理如下：

则：

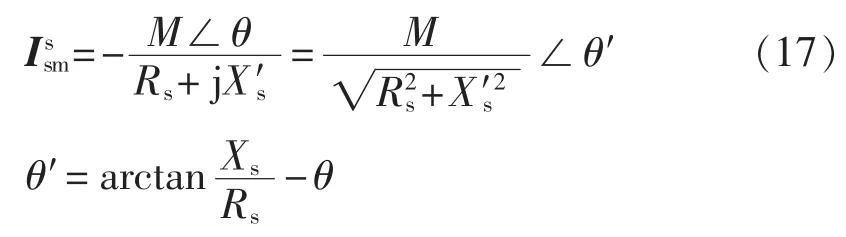
同理，不计励磁支路电流，得到转子坐标系下的转子电流为：

θ′经坐标变换后变为 θ″。 由式（17）、（18）可知，恒转子直流磁链作用下系统的有功功耗为：

式（8）表明转子暂态电流交流分量的幅值受Crowbar阻值影响，阻值越大，转子电流交流分量的幅值越小；式（18）表明转子暂态电流的直流分量幅值的大小与Crowbar电路的具体阻值无关。

由于定转子直流磁链的衰减速度主要取决于磁场储能的耗散速度，故本文采用式（11）和式（19）的有功耗散速率来表征定转子直流磁链的衰减速度。式（11）表明，当 Crowbar阻值大于 Rmcraoxwbar以后，定子直流磁链的衰减速度随着Crowbar阻值的增大而减小；式（19）表明，转子直流磁链的衰减速度随着Crowbar阻值的增大而增大。

1.1.2 仿真验证

研究Crowbar保护下DFIG动态特性时，以等值单机接无穷大系统机端三相短路为仿真研究对象，分析发电机自身参数及Crowbar阻值对转子电流及定转子直流磁链动态特性的影响，仿真模型如图1所示。

图1 等值单机接无穷大系统Fig.1 Equivalent single-generator connected to infinit system

Crowbar保护电路采用主动式结构，由晶闸管三相整流桥、IGBT开关元件及卸荷电阻构成。

仿真中，t=0.1 s时机端发生三相短路故障，Crowbar保护迅速动作，t=0.2s时退出，t=0.3s时故障切除，短路持续时间为200 ms。

图2和图3分别为定子和转子磁链幅值波形（文中图形纵轴均为标幺值），由图2知，t=0.1s故障发生时，定子磁链幅值逐渐减小，且随着Crowbar阻值的增大，定子磁链幅值的衰减速度也越慢，表明定子磁链直流分量的衰减时间常数越小。由图3知，Crowbar阻值越大，转子磁链幅值的衰减速度越快，对应的转子中暂态直流磁链的衰减时间常数越大。由于t=0.2s时Crowbar退出，转子变换器重新投入运行，故转子磁链幅值在t=0.2s时出现阶梯式增长。

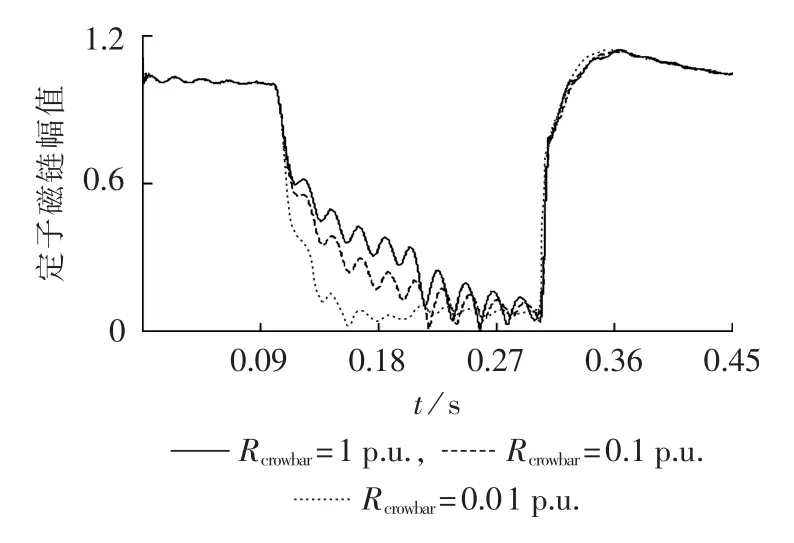
图2 定子磁链幅值Fig.2 Amplitude of stator flux

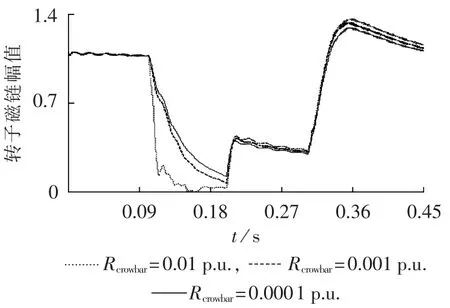
图3 转子磁链幅值Fig.3 Amplitude of rotor flux

由图2同时可以看出，不论Crowbar阻值的大小，t=0.3s故障切除时，定子磁链的幅值迅速突变到稳态值附近，故障切除时定子磁链中不出现直流分量。

图4 不同Crowbar阻值下转子三相电流波形Fig.4 Waveforms of three phase rotor currents for different Crowbar resistances

图4为Crowbar阻值取不同值时转子三相电流波形。0.1～0.2 s为故障期间Crowbar动作时段，0.2 s时Crowbar退出、变换器投入但故障仍未切除，0.3 s时故障切除，DFIG恢复正常运行。

图4（a）表明Crowbar投入后转子电流直流分量迅速衰减，只维持了Crowbar投入后初始时刻的几个波峰，而由于直流分量的快速衰减，转子电流中仅存在三相对称的交流分量，如图所示，Crowbar投运阶段转子电流为三相对称且缓慢衰减的工频交流电流。转子交流分量的缓慢衰减意味着定子直流磁链的缓慢衰减，当Crowbar退出时定子直流磁链未充分衰减，导致变换器重新投运后转子电流出现工频振荡成分，如图4（a）中0.2～0.3s时段的转子电流波形所示。未充分衰减的定子直流磁链及其相应的转子工频振荡电流会诱发Crowbar保护的二次动作，从而不利于Crowbar保护快速稳定地退出。

图4（c）中，转子电流交流分量的衰减速度较图4（a）中加快，而随着Crowbar阻值的减小，直流分量的衰减速度变慢，如图 4（b）、（c）中所示，随着Crowbar阻值的减小，转子电流直流分量越来越明显地“析出”，且0.2 s时Crowbar退出并未引起转子电流的振荡。

图4（b）中转子电流的交流分量和直流分量都取得了较为理想的衰减效果。

综上可知，在本文的仿真算例中，随着Crowbar阻值的增大，定子直流磁链的衰减速度减小而转子直流磁链的衰减速度增大，反之亦然。Crowbar阻值的选取存在一最优值，在此最优值附近定转子暂态直流磁链及其对应的转子电流的交直流分量均能得到迅速而有效的衰减，从而有利于Crowbar保护的快速退出。本例中，Crowbar阻值整定在0.01 p.u.附近时定、转子直流磁链均获得合适的衰减速度。

由理论分析与仿真波形可知Crowbar阻值的增大能有效抑制转子电流交流量的幅值，转子交流电流幅值的减小并不表示定子直流磁链衰减速度的增加。转子直流分量的幅值在图4中各Crowbar阻值下大致相同，表现为除去交流成分影响后转子电流初始时刻不对称偏移量的大致相同。这与式（18）的结论一致。

1.2 Crowbar阻值对电磁转矩和转子转速的影响

1.2.1 理论分析

经Crowbar短接转子的DFIG运行于普通异步感应发电机状态，其电磁转矩的表达式为[15]：

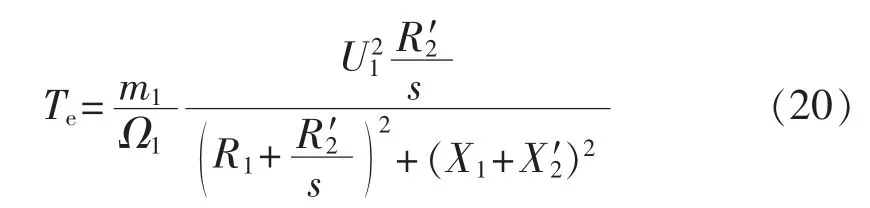
其中，m1、Ω1为恒定常数；U1为定子电压；s 为转差率；R1、R′2分别为定子绕组电阻和归算至定子侧的转子绕组电阻；X1、X′2分别为定子绕组电抗和归算至定子侧的转子绕组电抗。

由式（20）经推导可知，若U1和s为常数，当转子绕组电阻满足式（21）时，电磁转矩Te取得最大值。

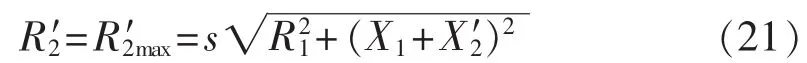
当R′2＜R′2max时，电磁转矩将随着转子电阻的增大而增大；当R′2＞R′2max时，电磁转矩将随着转子电阻的增大而减小。因此，Crowbar阻值对DFIG电磁转矩的影响亦应满足上述规律。

又知，Crowbar短接转子下DFIG的转子运动方程为[15]：

式（22）表明，当机械转矩Tm不变时，电磁转矩Te越小，则转子的转速升高得越快；由式（20）可知，异步机运行状态下DFIG的电磁转矩与机端电压U1的平方成正比，当电网电压跌落导致DFIG机端电压跌落时，电磁转矩将以平方于电压跌落程度的速率严重削弱从而使转子转速迅速上升，转子转速上升一方面会对DFIG的安全运行造成危害，另一方面会导致风机失稳。因此，采用Crowbar电路实现低电压穿越的DFIG在Crowbar电阻阻值选取的时候应使DFIG在低电压穿越的过程中获得尽量大的电磁转矩，以免由于电磁转矩不足而使转子过速。

1.2.2 仿真分析

仿真测试系统结构同图1。t=0.1s时无穷大电网电压发生跌落，Crowbar保护立即投入短接DFIG转子，t=0.35s时电网电压恢复正常。不同电网电压跌落程度、不同Crowbar阻值的情况下仿真得到DFIG电磁转矩Te和转子转速ωr的波形分别如图5—7所示。

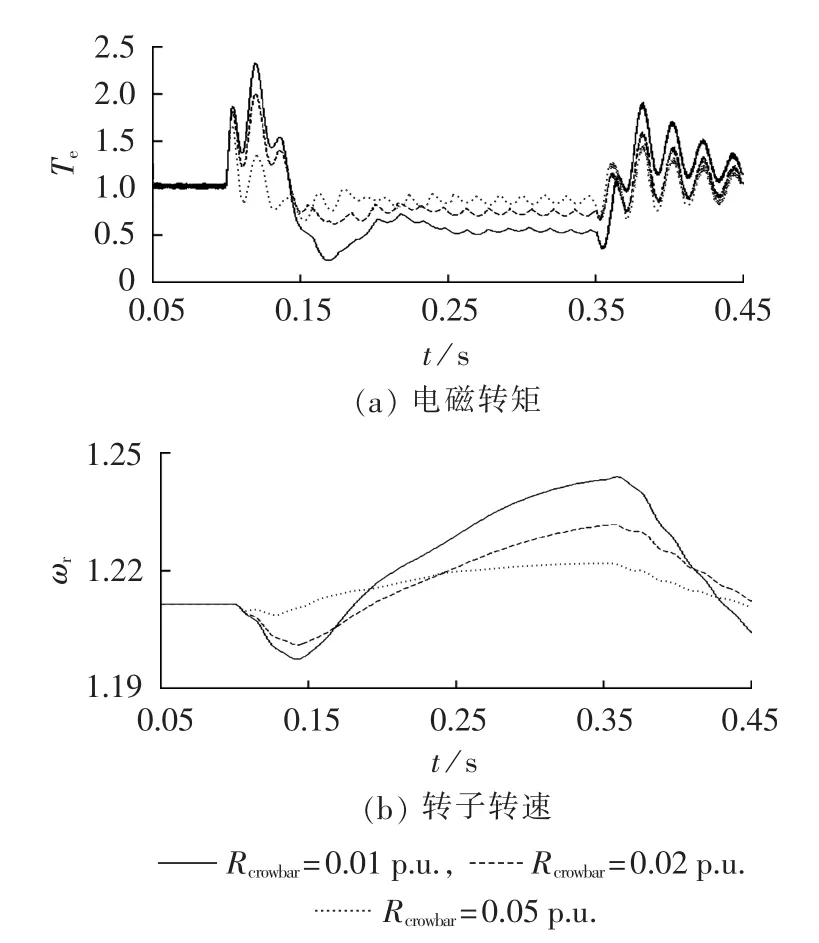
图5 电压跌落程度为-0.2 p.u.时不同Crowbar阻值下的电磁转矩和转子转速（1）Fig.5 Electromagnetic torque and rotor speed for different Crowbar resistances when voltage drops-0.2 p.u.（1）

图6 电压跌落程度为-0.2 p.u.时不同Crowbar阻值下的电磁转矩和转子转速（2）Fig.6 Electromagnetic torque and rotor speed for different Crowbar resistances when voltage drops-0.2 p.u.（2）

由图5（a）可以看出，短路发生瞬间电磁转矩出现剧烈波动，短路稳定后电磁转矩随着Crowbar阻值Rcrowbar的增大而增大。由图5（b）可知，转子转速的峰值随着Rcrowbar的增大而减小。

图7 电压跌落程度为-0.5 p.u.时不同Crowbar阻值下的电磁转矩和转子转速Fig.7 Electromagnetic torque and rotor speed for different Crowbar resistances when voltage drops-0.5 p.u.

由图6（a）可以看出，短路稳态下的电磁转矩随着Crowbar阻值的增大而减小。由图6（b）可知，转子转速的峰值随着Rcrowbar的增大而增大。

图5和图6的各曲线表明，当Rcrowbar＜0.05p.u.时，电磁转矩Te随着Rcrowbar的增大有增大的趋势，转子转速则相应地呈现减小的趋势；当Rcrowbar≥0.05p.u.时，电磁转矩Te随着Rcrowbar的增大有减小的趋势，而转子转速则呈现增大的趋势。

图5和图6中电磁转矩和转子转速的特性与理论分析相吻合，即Crowbar阻值存在一极限值R′crowbar，在此极限值下DFIG获得最大的电磁转矩，从而转子转速的增量最小；当Crowbar阻值大于或小于此极限值时，随着Crowbar阻值的增大或减小电磁转矩均将减小，从而转子转速的增量将增大。

由图7可以看出，当电压跌落程度为-0.5p.u.时，电磁转矩和转子转速与Crowbar阻值的关系表现出与图5和图6相似的变化特点。在3条曲线中，当Rcrowbar=0.05 p.u.时，DFIG获得最大的电磁转矩，其转速的增量也最小；当Rcrowbar=0.01＜0.05 p.u.和Rcrowbar=0.5＞0.05 p.u.时，DFIG的电磁转矩均减小，其转速的增量也均增大。

仿真结果证明了本文理论分析的合理性。基于上述分析可知，Crowbar阻值不宜选取得过大或过小，过大或过小的Crowbar阻值都将降低DFIG低电压穿越时电磁转矩的大小，从而削弱其低电压穿越能力。

2 附加串联电感的Crowbar电路

由1.2.2节中电磁转矩的波形可知，随着Crowbar阻值的减小，短路发生瞬间电磁转矩的波动也越剧烈。当Rcrowbar=0.05 p.u.时，DFIG获得最大的稳态低电压穿越电磁转矩，但短路发生瞬间的暂态过程中电磁转矩却出现了非常强烈的波动，电压跌落程度为-0.5 p.u.时波动峰值甚至达到了2.0 p.u.左右。电磁转矩的大幅波动会威胁到DFIG轴系的安全，而由理论分析可知，若是通过增大Crowbar阻值的方法抑制电磁转矩的暂态波动则会大幅削弱DFIG低电压穿越下的稳态电磁转矩，从而造成转子过速而不利于DFIG并网运行的安全稳定。

为解决这个问题，本文采用在Crowbar回路中附加串联电感来抑制电磁转矩的暂态波动，其原理如图8所示。附加电感L与一可控开关S并联后串入Crowbar电路的直流回路，S处于闭合状态时L被短路而不起作用，当S在控制信号的作用下打开时L与耗能电阻Rcrowbar串接在一起从而发挥作用。

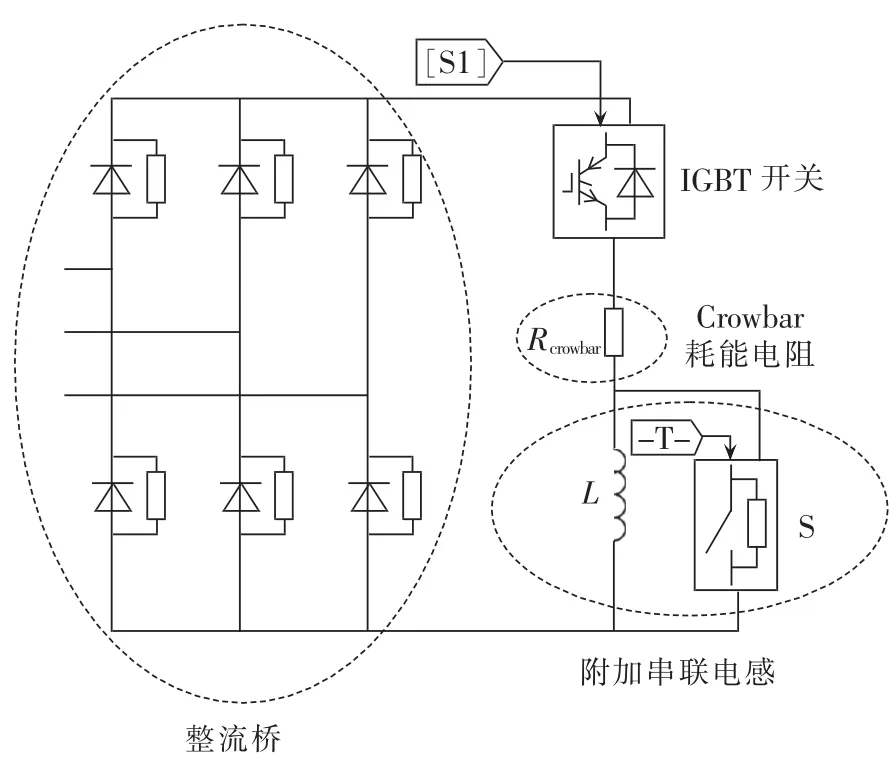
图8 附加串联电感Crowbar电路结构图Fig.8 Crowbar circuit with additional series inductor

加装串联电感前、后DFIG电磁转矩和转子转速的仿真波形分别如图9、图10所示。仿真系统结构同图1，t=0.1s时无穷大电网电压发生跌落，Crowbar保护立即投入短接DFIG转子，t=0.35s时电网电压恢复正常，Crowbar阻值取为Rcrowbar=0.05 p.u.。仿真中，串联电感在电压跌落发生瞬间与Crowbar电路一起投入，为避免转子串联电感对DFIG运行特性的不利影响，t=0.2s时串联电感退出运行，即串联电感只在短路发生后的瞬时暂态过程中投入运行以抑制电磁转矩的波动。

由图 9（a）和 10（a）可知，加装串联电感比未加装串联电感的DFIG电磁转矩的最大波动峰值小；由图9（b）和 10（b）可知，加装串联电感比未加装串联电感的DFIG转子转速的峰值小。

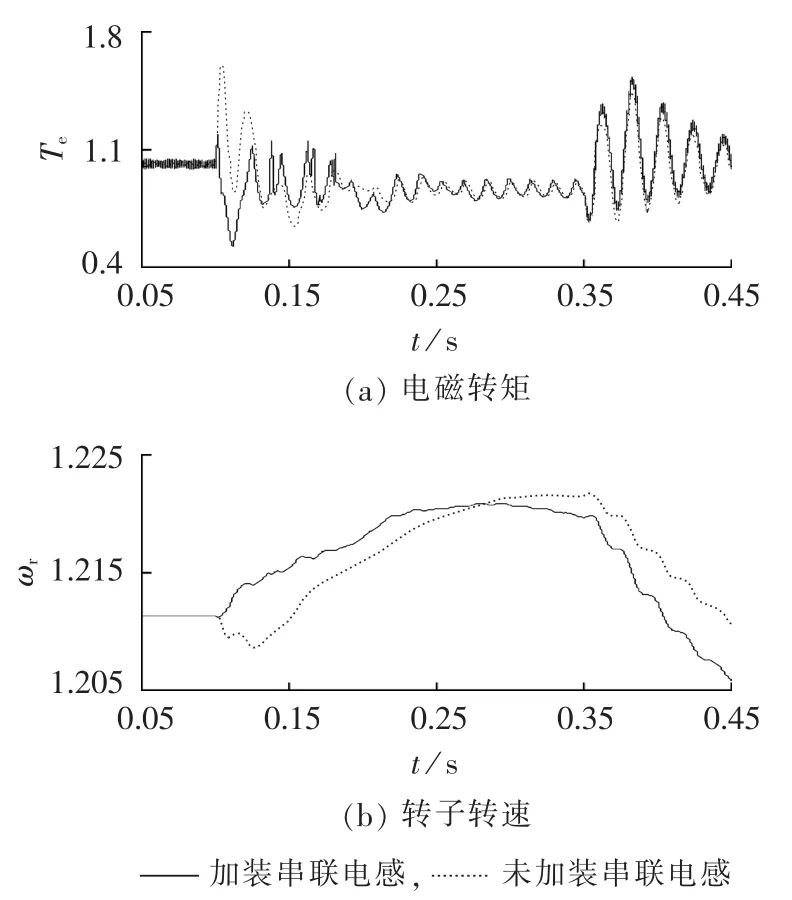
图9 电压跌落程度为-0.2 p.u.时加装串联电感前后电磁转矩和转子转速Fig.9 Electromagnetic torque and rotor speed when voltage drops-0.2 p.u.before and after adding series inductor

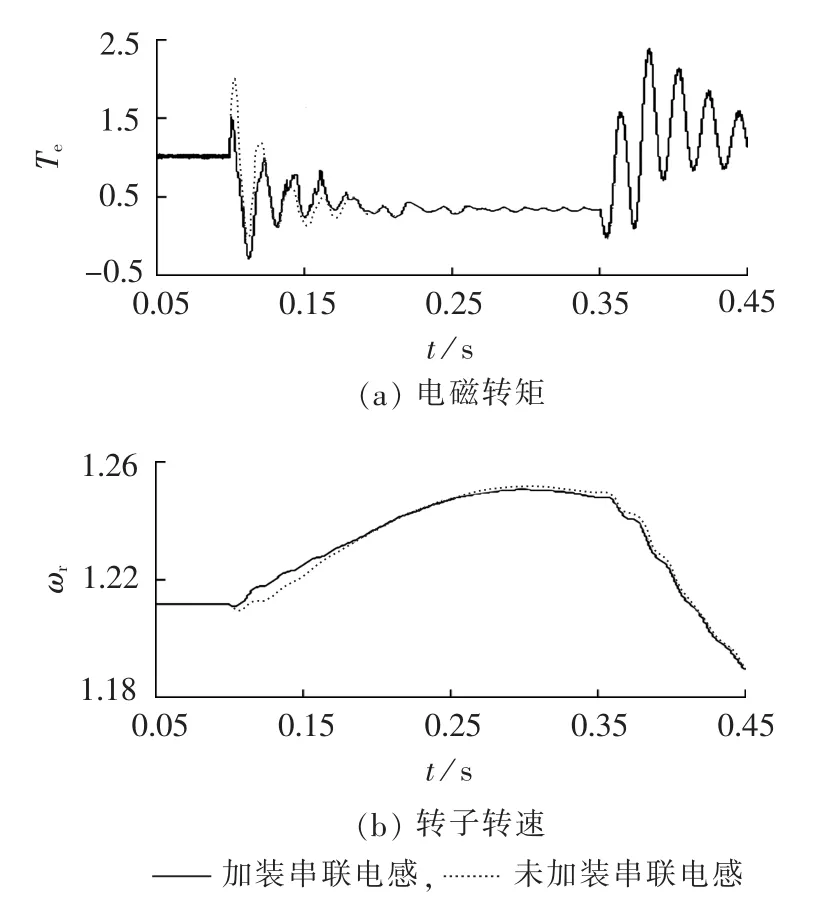
图10 电压跌落程度为-0.5 p.u.时加装串联电感前后电磁转矩和转子转速Fig.10 Electromagnetic torque and rotor speed when voltage drops-0.5 p.u.before and after adding series inductor

由此可知，通过在Crowbar回路中串联附加电感可以在一定程度上缓和电压跌落发生瞬间DFIG电磁转矩的波动，并可以轻微降低DFIG转子转速。但同时，转子回路中电感的串入会导致DFIG的电磁转矩波形中出现一定量的高次谐波，也会增加制造及控制的难度。由于风机带有的电力电子装置也会产生大量谐波，附加串联电感产生的高次谐波可与风机产生的其他谐波一起通过风机原有的滤波装置滤除。

3 结论

a.Crowbar阻值与DFIG定子直流磁链的衰减速度并非成正比关系，在一定情况下定子直流磁链的衰减速度随着Crowbar阻值的增大而减小，Crowbar阻值过大时会导致转子电流在Crowbar退出时出现“二次振荡”，不利于Crowbar电路的稳定投退。

b.Crowbar阻值存在“极限值”，在此极限值下DFIG电磁转矩最大，相应转速的增量也最小，低于此极限值时电磁转矩随着Crowbar阻值的减小而减小，高于此极限值时电磁转矩随着Crowbar阻值的增大而减小。

c.当其他条件满足要求时，Crowbar阻值的选取应尽可能地使DFIG获得最大的电磁转矩和最高的定子直流磁链衰减速度。Crowbar阻值过低会导致电压跌落瞬间电磁转矩产生剧烈的暂态振荡，通过在Crowbar电路中短时串联附加电感可以在一定程度上抑制电磁转矩的暂态振荡。