基于参数化潮流模型的可用输电能力改进算法

罗 钢,石东源,陈金富

（华中科技大学 强电磁工程与新技术国家重点实验室,湖北 武汉 430074）

0 引言

在中国建设特高压同步互联电网[1-6]的背景下，对于超大区域互联系统的运行与调度部门，可用输电能力（ATC）[7-8]正逐渐成为年度 /季度运行方式安排、日前调度计划制定、实时调度运行与控制所关注的重要指标。系统规模的扩大使得ATC计算的复杂性越来越高，对所采用算法的速度与精度也提出了更高的要求。

目前，在电力调度部门通常采用确定性的ATC计算方法，其基本过程可描述为：在功率注入空间中，从某一基本运行点出发，通过调整运行方式，在多种静态约束与动态约束共同确定的安全域内搜索极限运行点，将该点所确定的断面传输功率作为极限传输功率。不同的极限运行点搜索方法形成了如下不同的ATC算法：

a. 最优潮流（OPF）法[9-11]直接在安全域的边界上寻找理想的最优运行点，不考虑如何从基态到达该点，给出的是理想的目标方案，可能无法实现，且优化算法耗时较多；

b.连续潮流（CPF）法[12-14]在搜索过程中，沿预先确定的方向搜索到安全域边界上的某一点，即作为极限运行点，能够克服牛顿潮流法在电压稳定极限点的潮流不收敛问题，但预先确定的功率增长方向在计算过程中无法改变，所求结果忽略了发电和负荷的优化分布；

c.重复潮流（RPF）法[15-17]与 CPF 法类似，但其搜索过程无需明确指出搜索方向，具有一定的开放性，搜索结果可能是安全域边界上的任意一点，存在偶然性。

文献[18]针对大型互联电网的需求，充分发挥RPF法所具有的优势，改进其计算过程，提出了一种考虑方向性与风险性等多方面影响因素的ATC快速计算方法，但该方法未能解决以下3个方面问题：在ATC计算的功率调整过程中，极易出现潮流不收敛，导致计算效率低，且不能计算到真正的电压稳定极限点；在故障校验过程中，若故障后的稳态潮流不收敛，则只能简单地判定该故障下系统失稳，不能区分系统在故障后存在潮流解，且所采用的潮流计算工具无法找到该解的情形[19]；在多断面功率控制[20]中，当断面功率和目标值相差较大时，RPF法难以进行精确的功率调整，且极易出现潮流不收敛。

本文在文献[18]的基础上，将RPF法与CPF法相结合构建了主从迭代的改进算法，解决了潮流收敛性、稳定性以及功率调整的方向性问题，并将参数化潮流模型应用到故障校验与多断面功率控制中，解决了各自的收敛性问题。开发的软件在小型系统与大型互联电网中的应用算例验证了本文算法的有效性和实用性。

1 ATC计算模型与改进算法

1.1 目标函数及约束条件

ATC的计算模型可描述为：

其中，f为构成输电断面的各条线路传输功率求和函数；u和x分别为控制变量和状态变量；z为电网的拓扑结构变量；g和h分别表示等式和不等式约束；Ω为被考察时段内电网可能出现的运行方式集合。

上述模型是在多种约束条件下，寻求使区域间联络线传输功率最大化的运行方式，并保证可实现由初始运行点到极限运行点的功率调整过程。所考虑的等式约束条件包含基态和故障后的稳态潮流方程，不等式约束条件包含基态和故障后的节点电压限制、发电机出力限制、线路容量极限、静态电压稳定约束以及暂态稳定约束等。

1.2 CPF法与RPF法的特点

OPF法、CPF法与RPF法等多种算法被应用于求解式（1），其中后两者与OPF法相比，能够给出运行极限点的调整过程，保证计算结果的可实现性，且算法稳定，计算效率高，更适于在大型互联电网中应用。

图1所示为基于CPF法与RPF法的ATC计算过程示意图。图中，Pi、Pj为节点的注入有功功率；M1为暂态安全域的边界；M2为静态安全域的边界；S0、S11、S12、S21、S22为系统运行状态点。 S0—S12—S22是基于 CPF 法的潮流轨迹计算过程[13]，S0—S21—S11是基于改进RPF法的潮流轨迹计算过程[18]，二者具有以下特点。

图1 ATC计算中的潮流轨迹Fig.1 Power flow trajectories in ATC calculation

a.CPF法从初始状态S0出发，沿着预先确定的功率增长方向计算新的潮流解点，逼近静态/暂态约束极限点。该方法所求取的ATC结果将直接依赖于初始功率增长方向的选取，其计算结果只是一个可行解，而未必是系统运行人员真正关心的解。

b.RPF法的功率增长过程中，其方向与步长均可灵活选择。文献[18]将潮流轨迹分解为若干段，每一段利用线性分布因子分别计算功率增长方向，由此逼近运行人员关心的方向，得到满足实际需求的ATC结果。但是，潮流问题本身是多解的，由1个稳定解和多个不稳定解组成[21]，基于RPF法的分段潮流轨迹计算过程无法保证从初始运行点沿着稳定的解曲线前进，可能在多组不稳定的解之间来回跳动，导致不合理的结果。为了提高计算效率而选取较大的功率增长步长时，极易造成潮流不收敛。此外，由于潮流雅可比矩阵奇异，RPF法无法计算到真正的静态稳定极限点。

1.3 主从迭代的ATC改进算法

综上所述，CPF法的功率增长过程能保证潮流解的稳定性与可实现性，但却存在方向性问题；RPF法可以很好地解决方向性问题，但却无法保证潮流的收敛性与解的稳定性。为此，本文将2种方法进行融合，以RPF法为框架，将CPF法内嵌，构成了主从迭代的ATC改进算法。

1.3.1 RPF法主迭代环节

RPF法主迭代环节的核心是将潮流轨迹分解为若干段，逐段修正潮流调整方向与步长，进而逼近预设方向。分解后的ATC计算模型可描述为：

其中，n 为迭代次数，n=1，2，…，N；N 为最大迭代次数；dn为第n次迭代时的功率单位增长量，即功率调整方向；Δpn为第n次迭代时的功率调整步长。

式（3）中 dn与 Δpn可通过优化算法[22]或线性化[18]的方法计算得到。考虑到ATC计算时既要保证系统的安全性也要保证系统的经济性，文献[18]给出了3种在电网运行与调度中具有实际意义的功率调整方向：最保守方向、乐观方向以及最经济方向，运行人员可根据需要灵活选择。

RPF法主迭代过程从初始潮流解点出发，按照式（3）调整节点注入功率并求解潮流方程，依次得到下一个潮流解点，再校验式（2）给出的各种约束条件。对于任意迭代步，如果潮流收敛，则进行潮流合理性调整，调节无功补偿设备或变压器变比，将元件的越限电气量调整到允许的范围，并重新计算潮流，直至得到的潮流解点满足系统的运行要求，由此保证潮流解的稳定性；如果RPF法计算不收敛，则可能是由于迭代步长过大或潮流接近静态稳定极限点，此时RPF法计算存在困难，转入CPF法迭代过程。

1.3.2 CPF法从迭代环节

将RPF法第n个迭代步的dn与Δpn作为CPF法计算的功率调整方向与调整目标，建立参数化潮流模型：

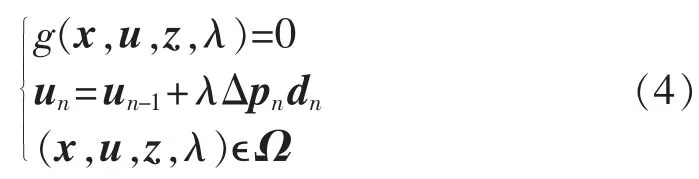
其中，λ为连续化因子。

采用局部参数化方法[23]，选取状态变量中变化最快的分量构造扩展方程：

其中，xkj为CPF法迭代过程中第j个潮流解点处状态变量x中变化最快的分量xk的取值；xkj-1为第j-1个潮流解点处xk的取值；Δxkj为第j个潮流解点处xk的迭代步长。

式（4）中，λ=0与RPF法主迭代过程的第n-1个解点相对应，λ=1则是第n次迭代的目标解点。联立式（4）、式（5），进入 CPF 法从迭代过程，通过预测环节-校正环节的迭代得到一系列随参数λ变化的潮流解点。如果能够找到λ≥1的运行点，则表明按照dn与Δpn调整节点注入功率后系统仍然能够保持静态稳定，在λ=1的解点处结束从迭代过程，返回RPF法主迭代过程。如果求取的λ最大值小于1，则表明系统已到达鼻点，由此求得了系统的静态电压稳定极限点，返回主迭代过程。

需要指出的是，为了尽可能减少约束校验的次数，满足在线计算的要求，在CPF法的从迭代过程中，对于中间潮流解点并不进行静态与暂态约束校验，仅对返回主迭代过程的最终解点进行校验。

主从迭代的ATC改进算法保持了RPF法灵活开放的特点，并利用CPF法提高了算法鲁棒性，不仅解决了各自算法的缺陷，而且具有较高的计算效率。计算流程如图2所示。

图2 潮流解点计算流程图Fig.2 Flowchart of power flow point calculation

1.4 基于CPF法的静态约束校验

获取潮流解点后，需要校验基态与故障后系统能否保持静态稳定性，并在此基础上检验静态安全性约束是否满足。对于预想故障集下的N-1校核，如果潮流不收敛，则难以准确判断系统故障后的静态稳定性。这是由于系统故障后无法找到稳态潮流解的情形有2种：一种是系统确实失稳；另一种是系统在该故障下存在潮流解，但所采用的潮流计算工具无法找到该解。如果简单地判定系统失稳，则可能造成误判。为此，本文将电网拓扑结构变量参数化，构建连续潮流模型来区分上述情形，如下式所示：

其中，zi0为元件故障前的参数。

式（6）中，λ=0与系统无故障的潮流状态相对应，λ=1与该元件故障后被完全切除的系统状态相对应。式（6）与式（5）联立构成扩展参数化潮流方程，利用CPF法求解该模型，如果能找到λ≥1的稳态运行点，则表明该故障下系统能够保持静态稳定，λ=1即是故障后的稳态潮流解；如果求取的λ最大值小于1，则可判定该故障下系统将失去静态稳定。

1.5 基于CPF法的多断面功率控制

多断面功率控制是在大型互联电网中调整多个联络断面的功率至指定值，应用于ATC计算中考察相关断面对指定断面功率传输的影响。然而，现有计算方法在当前断面功率与目标功率偏差较大时，功率控制过程极易出现潮流不收敛，导致计算时间与调整精度难以满足运行人员的需求。为此，本文将断面功率参数化，建立CPF模型来解决上述问题。下文以单断面功率控制为例，多断面功率控制只需构建类似的扩展潮流方程联立求解。

首先，确定参与调整的发电机与负荷群，计算功率调整方向，在此基础上构建系统的潮流方程及与被控断面相关的有功功率偏差方程，如下式所示：

其中，L为组成被控断面的线路集合；Pl（k）为当前潮流状态下线路k的有功功率；PS0、PS1分别为被控断面的初始有功和目标有功功率；u0为控制变量的初始值；d为功率调整方向；γ为参数化因子。

式（7）中，γ=0为初始潮流状态，γ=1为潮流调整的目标状态。将式（7）与式（5）联立构成扩展参数化潮流方程，其中λ看作与x类似的状态变量，而γ作为被求的连续化参数。利用CPF法求解上述模型，如果能够找到γ≥1的运行点，则表明可以将断面功率控制在目标值，且γ=1对应的潮流解即是目标状态；如果求取的γ最大值小于1，系统已到达鼻点，则表明调节指定的发电机/负荷群并且在预先计算的功率增长方向下不能将断面功率调整到目标值，需要重新选定可调元件或改变功率增长方向。

2 ATC改进算法流程

构建大型互联电网计及静态与暂态安全稳定约束的ATC计算流程，如图3所示，主要包含多断面功率控制、潮流解点计算、静态安全与稳定约束校验、暂态稳定约束校验4个部分。前3个部分已在第1节讨论，本文所考虑的暂态稳定约束是指预想故障集下的暂态稳定性，采用时域仿真法校核。考虑到暂态稳定的时域仿真耗时较长，本文优化了约束校验过程。如图1所示的潮流轨迹S0—S21—S11，从S0计算到S21的过程中仅校核静态安全、稳定约束，得到静态极限点S21后，再校验暂态稳定，并反向调整节点注入功率，直至暂态稳定极限点S11，由此大幅减少了暂态稳定的校核次数，缩短了计算时间。

3 算例及分析

3.1 小型电网算例

在CEPRI 36节点系统上测试本文提出的改进算法，系统接线如图4所示，区域1与区域3分别经断面1和断面2向区域2送电。在系统送端的发电机母线2、3、7、8处各增加一台发电机。计算某断面ATC时，通过增加送端发电机出力、减少受端发电机出力来调整断面功率，同时保持外部区域的发电机出力不变。

图3 ATC计算流程图Fig.3 Flowchart of ATC calculation

图4 CEPRI 36节点系统分区图Fig.4 Partition diagram of CEPRI 36-bus system

a.ATC计算结果与过程分析。

表1给出断面1、断面2在不同功率增长方向下的ATC计算结果。表2给出断面1计算中，区域1与区域2的发电机有功功率调整结果，表中G1表示与母线1相连的发电机，其他类似，G2-1与G3-1为原有发电机，G2-2、G3-2为新增发电机。按照保守、乐观、经济的功率增长方向得到的ATC计算结果不同，各方向下的发电机有功功率调整结果也存在较大差异。主要原因是不同的方向对应调整过程中不同的发电机有功功率分配比例，反映出不同的发电机对系统静态、暂态安全稳定约束的影响程度不同。因此，本文算法在主迭代过程中考虑方向性影响对于电网运行与调度具有实际意义，克服了CPF法在功率调整方向上的缺陷。

表1 3种功率增长方向下的ATC结果Tab.1 Results of ATC calculation for three power augment directions

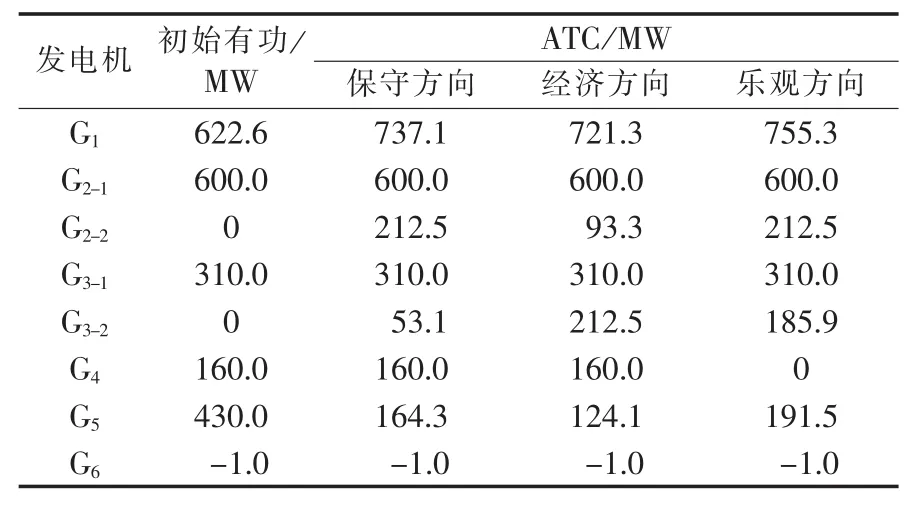
表2 发电机有功功率调整结果Tab.2 Results of generator active power adjustment

在断面1采用乐观方向计算ATC时，当发电机G2-2与G3-2有功功率分别从0增加到212.5 MW与215 MW时，利用RPF法迭代计算时，潮流不收敛；进入CPF法的迭代过程，求取的功率增长因子最大值为0.94＜1，此时系统已经达到静态电压稳定极限点，对应的断面传输功率增长量即是所求ATC结果。由此可见，本文的改进算法克服了RPF法在潮流不收敛时遇到的困难，且能计算到真正的电压稳定极限点。

b.故障校验分析。

全网的17条交流线路构成系统的N-1故障集，其中线路25-26在初始状态下开断即造成系统失稳，从故障集中剔除。在断面1的ATC计算过程中，对某个潮流解点进行N-1电压稳定约束校验时，发现其中3条线路开断将导致潮流无解，分别是线路19-30、23-24、27-28。对这些线路采用CPF模型计算连续化因子最大值λmax的结果分别为 0.87、1.24、1.15。 其中，线路 23-24、27-28 的 λmax大于 1，故开断这2条线路时系统实际上能够保持电压稳定性，而线路19-30的λmax小于1，该故障是真实的系统失稳故障。由此可见，本文故障校验模型能够很好地区分计算过程中潮流无解所对应的2种情形。

c.断面功率控制分析。

断面1传输的初始有功为611.6 MW，设定控制目标为1000 MW，选取待调整的控制变量为区域1与区域2的发电机出力。选取功率增长方向为保守方向，则采用本文的断面功率控制方法求得断面功率参数化因子γ的最大值为0.83＜1，可知按照保守方向无法将断面1的传输功率调整到目标值。重新选定乐观的功率调整方向，此时γ最大值为1.25＞1，可知按照乐观方向可实现断面1的调整目标，γ=1对应的潮流解点即是所求目标状态。

3.2 大型互联电网算例

在华北—华中联网系统上测试本文的改进算法。联网系统规模为：节点约15000个，发电机约1600台，交流线路总计约20000条，变压器总计约20000台，直流线路12条。其中华中电网以三峡水电站为中心辐射5省1市，共6个主要断面。在夏季水电大发时，华中电网经特高压断面向华北电网输送有功功率2058 MW，图5为系统结构及初始潮流示意图，图中数据单位为MW。

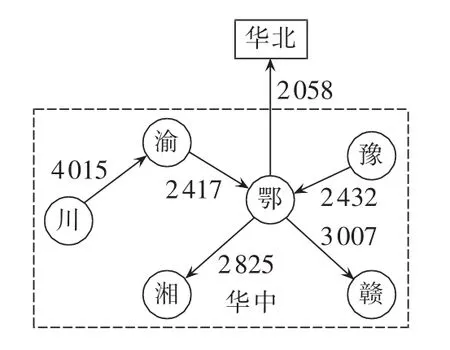
图5 华北—华中联网系统结构图Fig.5 Structure of North China-Central China Power Grid

采用以下3种算法分别计算特高压断面的ATC。

算法1：本文所提出的改进算法，控制华中电网内部各联络断面的传输功率到指定值，按照保守方向调整节点注入功率。

算法2：文献[18]提出的改进RPF法，不控制其他断面的功率，按照保守方向调整节点注入功率。

算法3：文献[13]提出的CPF法，控制华中电网内部各断面的传输功率到指定值，按照预先确定的保守方向调整节点注入功率，并保持该方向不变。

计算结果及耗时见表3。易见，3种算法的计算速度都较快，能够满足实际电网的在线计算需求。

表3 特高压断面的ATC计算结果Tab.3 Results of ATC calculation for UHV cross-section

算法1、算法3的ATC结果受暂态稳定限制，算法2的结果受静态稳定限制。这是由于该系统对于普通牛顿潮流算法的收敛性较差。采用算法2，当特高压断面传输功率达到2638 MW后，继续增加送端节点注入功率则潮流不收敛，此时算法2判定系统已达到静态稳定极限，而对该点进行的暂态稳定校验全部通过，最终得到受静态稳定限制的ATC结果。然而，采用算法1、算法3时，CPF模型能够计算到真正的静态电压稳定极限点，分别为3 017 MW、3 062 MW，此时预设故障下的暂态稳定校核不通过，即暂稳越限，按照算法流程应反向计算，逼近暂态稳定极限点，得到最终断面传输极限分别为2744MW、2851MW。由此可见，本文的改进算法对于潮流收敛性较差的系统同样适用，且能够计算到真正的静态稳定极限点，而直接采用RPF法的算法2在潮流收敛性较差系统中计算时得到了不正确的ATC结果。

最保守的功率增长方向实际上是只考虑系统的安全性要求，求取最不利情况下的ATC最小值。而表3中，算法1的结果小于算法3，说明算法1得到了更加不利情况下的ATC结果，更符合运行人员的实际需求。造成上述结果的原因是算法3受限于CPF法的功率调整过程，仅根据初始潮流状态选取保守的功率增长方向，并在计算过程中保持不变，而该方向与实际系统的最保守功率增长方向存在偏差，将造成ATC结果偏大。而算法1计算过程中不断根据新的潮流解点调整功率增长方向，由此逼近最保守方向，所求结果也更加接近真实的最保守方向下的ATC。由此进一步验证了改进算法相比于CPF法在功率调整方向上所具有的优越性。

综上所述，本文的改进算法同时克服了RPF法与CPF法的缺陷，对于大型互联电网具有较好的适应性。

4 结论

在中国建设特高压大型同步互联电网的背景下，本文从区域电网运行与调度的实际需求出发，提出了一种基于参数化潮流模型的大型互联电网ATC快速计算方法。该模型充分发挥了RPF法与CPF法的优势，在功率调整过程、潮流解点计算、约束校验以及多断面功率控制等方面利用参数化潮流模型改进了原有算法，解决了功率调整方向性、潮流收敛性、潮流解点稳定性等问题。改进算法能充分考虑多种影响因素，计算速度快，且对潮流收敛性较差的系统也具有良好的适应性。最后，通过算例验证了本文改进算法的有效性与实用性。