基于积分- 积分判据的电力设备IOS分析及应用实例

秦博宇,张雪敏,魏东宁

（清华大学 电机系 电力系统及发电设备控制和仿真国家重点实验室,北京 100084）

0 引言

输入-状态稳定（ISS）理论是由Eduardo D.Sontag和Yuan Wang等学者提出的，将状态空间稳定理论与输入输出稳定理论结合起来。通过研究“分解”的子系统的稳定属性判断互联系统的稳定性[1]，为网络的快速重构和紧急控制提供方便的稳定估计是该方法的重要优点。ISS理论已经在编队控制[2]、化工过程分析[3]、模型简化[4]以及控制器设计[5-6]、航天器姿态控制[7]、计算机网络[8]等方面得到了应用，显示出了广阔的应用前景。

电力系统暂态稳定分析的基本方法可以分为2类，即时域仿真法和暂态能量函数法。电力系统的高维性和强非线性特性将导致时域仿真法的计算量大，耗时长。文献[9-10]将半张量积方法推广和应用于独立电力系统暂态稳定分析问题，通过多项式近似系统求出了独立电力系统的稳定域。然而独立电力系统具有网络拓扑多变、单个设备模型复杂、存在外部持续扰动等特点，只研究不含扰动、初值给定的系统的Lyapunov稳定性并不能满足实际工程要求。因此有必要引入ISS理论来分析独立电力系统的稳定性。

文献[11]指出利用ISS理论可通过子系统的稳定性判断互联后系统的稳定性，这对于独立电力系统的设计和运行具有重要意义。而如何得到设备的ISS属性是其基础。对于子系统ISS属性的分析，关键在于如何估计增益函数。在现有研究中，一般是通过人工观察法得到，这给该理论的应用带来了不便。文献[12]研究了局部ISS属性、局部ISS-Lyapunov函数以及局部小增益条件，该研究使得ISS理论更接近工程实际。文献[13-16]介绍了一种基于子系统数学模型分析ISS属性的算法，但由于实际系统难以精确建模，对于规模较大的系统难以降阶，数学模型不易考虑实际系统中的限幅环节等原因，该方法具有一定的保守性。文献[17]介绍了一种基于试验测定系统L2增益的方法，其提出利用优化算法修正输入信号以减少量测噪声的影响。文献[18]给出了ISS理论的等价形式——积分-积分估计。对于一个ISS的子系统，可以用这2种等价的定义形式进行增益函数的估计，但目前尚无文献讨论哪种定义形式易于估计增益函数、哪种定义形式估计误差小。

本文首先介绍ISS的基本概念，给出基于积分-积分估计的ISS的等价定义式。为避免实际系统建模的复杂性，利用仿真分析子系统的ISS属性，根据实际物理系统选取几组典型的信号作为干扰输入，利用PSCAD仿真软件对发电机、电动机子系统的稳定属性进行估计。最后，通过仿真分析L∞范数形式和积分-积分估计形式的增益函数对于不同类型的输入信号的适应性。

1 ISS基本概念

1.1 局部输入-状态稳定（LISS）和LIOS的L∞范数定义

首先介绍文中出现的3类函数的概念。

K类函数：

K：=｛θ：R+0R+0连续，严格单增，θ（0）=0｝

K∞：=｛θ∈K无界｝

KL：=｛σ：R+0×R+0R+0连续，对一固定t≥0，

σ（·，t）∈K；对一固定 s≥0，σ（s，·）随 t∞，

严格衰减至0｝

定义1[14]对系统

若存在βISS∈KL，γISS∈K∞，ρ＞0，对任意有：

则称系统式（1）LISS。其中，x0为系统状态变量的初值；‖u‖为该系统的输入的无穷范数；γISS为系统式（1）的输入-状态增益。

定义2[14]对系统

若存在 βIOS∈KL，γIOS∈K∞，ρ＞0，对任意，‖u‖≤ρ有：

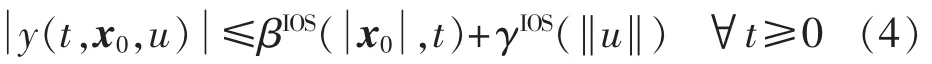
则称系统式（3）局部输入-输出稳定（LIOS）。其中，γIOS为系统式（3）的输入-输出增益。

1.2 积分-积分估计

文献[18]给出了ISS的等价形式，即积分-积分判据。

定义3[18]对 于任何一个初始状态x0以及输入u，系统满足不等式

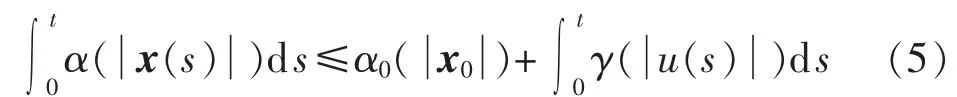
则称系统满足积分-积分估计。 其中，α，α0，γ∈K∞。

定理1[18]一个系统是ISS的当且仅当它满足积分-积分估计。

因此，可以用式（5）代替ISS的定义式，以积分能量衡量信号的大小。那么，子系统式（3）满足LISS和 LIOS 可表示为：存在 α，α0，γ∈K∞，Xlim＞0，Ulim＞0，对任意，有：

2 积分能量的计算

第1节介绍了ISS理论的等价形式（积分-积分估计），利用积分衡量输入与输出的大小，如何计算输入、输出的能量是关键所在。本节将对比2种积分能量的表达式：平衡点型积分能量函数、稳态运行区间型积分能量函数。

2.1 平衡点型积分能量函数

基于Lyapunov稳定理论的暂态稳定分析方法是系统安全分析和控制的重要基础。其以平衡点作为参考，实际工程中最关心的是当时，系统能否回到平衡点的稳定性，即，其中为平衡点。 类似地，可定义以下积分能量：

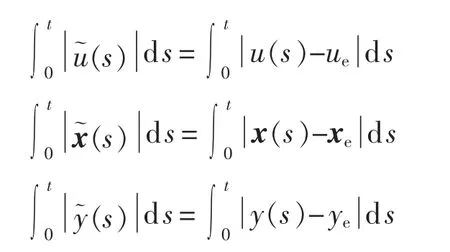
其中，ue、xe、ye分别为子系统输入、状态变量以及输出的平衡点。

参考平衡点计算积分能量会带来以下问题：

a.实际系统随着运行工况的变化，其平衡点也在不断变化，若给定每个子系统固定的平衡点，在互联条件改变时，平衡点的变化将导致积分趋于无穷；

b.若希望计算得到子系统的准确平衡点，则需要知道互联系统的具体形式，进而根据互联系统求得子系统当前工况下的平衡点，如此ISS理论希望将子系统稳定性的分析与互联系统稳定性分析解耦的思路难以实施；

c.实际系统稳态运行时，系统状态在平衡点处会出现小幅振荡，而不会严格等于平衡点的值，因此参考平衡点进行积分，在稳态情况下由于系统状态小幅振荡的缘故，积分能量会持续上涨，可能对计算结果有影响。

2.2 稳态运行区间型积分能量函数

基于第2.1节的分析，可以考虑改变计算积分的方式。实际系统运行中，经常利用反时限保护装置对系统的异常状态作出响应。国内外常用的反时限过电流保护的通用数学模型的基本形式为[19]：

其中，I为故障电流；Ip为保护启动电流；r为常数，取值通常在0～2之间；k为时间整定系数，单位为s。

当I＜Ip时，设备可以长时间连续运行；假设r=1，当 I＞Ip时，由式（7）可得 （I-Ip）t=kIp，等式右端为一常数，左端表示了过电流大小与时间成反比。如果考虑动态过程，可得到如下积分形式：

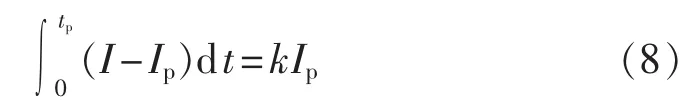
当t=tp时，认为保护装置动作。

综上，实际保护装置存在一个稳态运行区间，系统状态变量在此区间内，系统可以连续运行，当变量偏离稳态运行区间时，偏离程度越大，则允许运行时间越短。这不仅反映了变量的幅值信息，还反映了变量持续时间长短带来的影响，因此可以利用积分来近似这一过程。规定系统状态变量的稳态运行区间，若系统运行过程中某些状态变量超出稳态运行区间，则视为非正常状态，保护装置响应，即开始积分，该积分能量表示系统在非正常状态下的能量积累过程。例如，规定系统电压稳态运行区间为[0.9，1.1]p.u.，保护装置规定电压不得低于0.7 p.u.运行超过10 s，此时积分能量为，该能量是系统的极限能量。当系统积分能量超过极限能量时，认为保护装置动作，此时系统不能稳定运行。

规定输入、状态、输出变量的稳态运行区间分别为[UL，UU]、[XL，XU]、[YL，YU]，其中，下标 L、U 分别表示稳态运行区间的下界和上界。利用稳态运行区间作参考的积分能量分别定义如下：

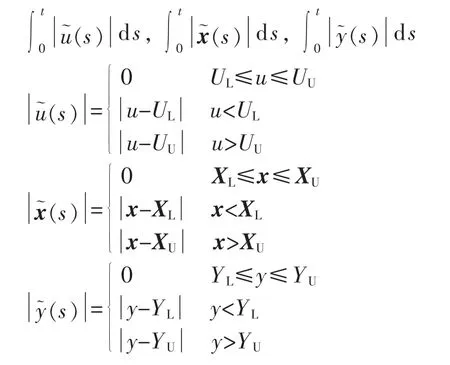
3 子系统LISS和LIOS的估计方法

文献[17]中介绍了基于试验测定线性系统L2增益的方法，利用线性系统的特殊性质，将求解使得增益最大的输入信号转化为求解一组优化问题。本文所研究的子系统具有强非线性，因此文献[17]中的方法并不完全适用，但其利用试验避免详细建模的思路是值得借鉴的。本节介绍一种基于PSCAD仿真实验的子系统增益函数的近似估计方法。

这里需要指出，本文考察的是使得子系统状态变量x和输出y都稳定的输入信号，在这样的条件下，子系统是LISS和LIOS的。由于互联系统的稳定分析不需要系统LISS的增益函数，以下仅介绍子系统LIOS增益函数的估计方法。

3.1 输入信号

本文考虑输入在一定范围内的LISS和LIOS问题。实际互联的独立电力系统中，一个子系统的输入是另一个子系统的输出，干扰主要来自与该子系统互联的其他子系统，因此考虑采用工频正弦波作为干扰输入。考虑到实际系统启动会伴随状态变量的冲激，根据包络线的不同，定义以下4种输入信号：

a.矩形输入信号（干扰持续一段时间后回到平衡点）；

b.矩形带冲激输入信号（矩形干扰持续时间内出现冲激）；

c.阶跃输入信号；

d.阶跃带冲激输入信号。

3.2 增益函数的估计方法

对子系统进行ISS属性分析，关键在于增益函数的估计。下面将根据LISS与LIOS的定义式，利用仿真方法对L∞范数定义形式与积分定义形式的LIOS增益函数进行讨论。

对于L∞范数定义式，需要估计KL类函数β以及K∞类函数γ；对于积分定义式，需要估计K∞类函数α0和γ。本文假定β是指数函数，α0、γ为线性函数，其函数表达式如下：

利用仿真估计子系统增益函数的方法如下。

步骤1选择所研究子系统的状态变量x以及输出y。

步骤2参考系统的保护配置，给定子系统可持续运行区间，并根据保护的整定值给出积分能量的上限值。

步骤3给定输入信号u，固定系统的初始状态x0，得到输出 y。

对于L∞范数定义情况，输出取稳态值，即t ∞，此时β=0，近似估计输入-输出增益：

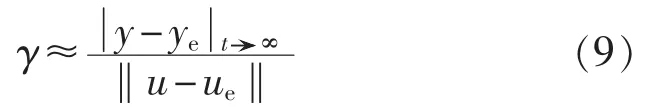
步骤4改变输入的大小或采用不同形式的输入，用步骤2的方法计算输入-输出增益，可以得到一系列的γ，从中取最大的γmax近似子系统的输入-输出增益。若系统状态变量和输出的积分能量值超过上限值，那么认为此时系统失稳；逐步减小输入直至系统稳定，估计子系统输入信号的范围。

步骤5确定γmax后，在规定的范围内改变系统的初值以及输入。对于L∞范数定义形式，利用指数函数进行拟合，例如取最大值时的点以及末端的稳定点2个点进行拟合：时刻分别为 tmax、tend，幅值分别为 βmax、βend。 可以得到：

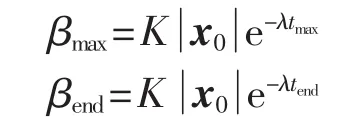
从而可以计算得出函数的待定系数：

对于积分定义形式：

改变初值，可以得到不同的α0函数，取其中最大的α0作为估计。

4 发电机与电动机子系统仿真分析

前文介绍了LISS和LIOS的基本概念以及如何利用仿真估计子系统的增益函数。本节首先介绍独立系统典型设备发电机、电动机的仿真模型，通过对发电机和电动机子系统的仿真分析，比较L∞范数定义形式与积分定义形式的适用范围。

4.1 子系统仿真模型

本节通过PSCAD仿真计算发电机以及电动机的LIOS属性。利用仿真获取发电机及负载的LIOS属性，意味着要将发电机的负载虚拟成一个电流源，将负载的电源虚拟成一个电压源。如何合理地设置仿真环境是一个关键。下面就PSCAD仿真模型做简要说明。

a.发电机以转速ω、暂态电动势E′q以及励磁和调速控制器的相关控制变量作为状态变量；电动机以转差率s作为状态变量。发电机子系统选取机端电压的标幺值作为输出，外加干扰电流源为输入；电动机子系统选取机端电流为输出，外加干扰电压源为输入。

b.发电机子系统的状态变量初值x0取自电阻负载切除之前，即发电机外接可控干扰电流源接入时的数值；电动机子系统的状态变量初值X0取发电机切除之前，即电动机外接可控电压源接入时状态变量的稳态值。

c.子系统外加干扰源的角频率始终与子系统的角频率相同（包括暂态过程）。在PSCAD中通过锁相环可以实现。这一处理是考虑实际系统中负载和电源的电压、电流量是同一频率，即以工频分量为主。

d.规定发电机电压稳态运行区间为[0.9，1.1]p.u.，规定电动机电流可持续运行范围为[0，1]p.u.。

e.此处规定保护整定为发电机机端电压不得低于0.7 p.u.运行超过8 s，即发电机机端电压积分上限值为：

电动机电流不得高于4 p.u.运行超过10 s，即电动机输出电流积分上限值为：

发电机的主要参数为：额定相电压3.81 kV，额定相电流1.05 kA，基准角频率314.159 rad/s，Xd=0.92 p.u.，X′d=0.3 p.u.。 电动机的主要参数为：额定相电压0.22 kV，额定相电流3.2 kA。

4.2 发电机子系统输入-输出增益估计

分别利用阶跃、矩形、矩形带冲激信号作为输入，其输入电流有效值和输出电压有效值（标幺值）波形如图1所示，计算得到发电机子系统的输入-输出增益如表1所示。

图1 发电机子系统输入电流和输出电压波形Fig.1 Input current and output voltage waveforms of generator subsystem

表1 发电机子系统输入-输出增益Tab.1 Input-to-output gain of generator subsystem

表1中，用L∞范数定义形式计算出的输入-输出增益差异较大，利用积分-积分形式估计的输入-输出增益差异较小。情况1的输入为阶跃信号，用L∞范数表示为‖u‖=3 kA，仿真结果为系统振荡失稳。情况2、3利用矩形信号，幅值均为3 kA，持续时间不同，用L∞范数表示为‖u‖=3 kA，系统可以稳定运行，说明仅反映信号幅值信息是不够的。由于情况2—5的输入信号最终都回到平衡点附近，输出的稳态值也在平衡点附近，对于L∞范数定义形式根据式（9）计算输入-输出增益时利用输出的稳态值，因此输入-输出增益主要取决于输入的大小，情况2、3的矩形输入信号虽然持续时间不同，但幅值相同，用L∞范数衡量输入的大小相同，因此计算出的输入-输出增益相同；当输入带有冲激时，如情况4、5，用L∞范数衡量输入的大小有较大差别时，会使得计算出的增益差别较大。

积分定义形式利用积分能量衡量输入、输出，对于信号的不同能有一个合理的反映，因此其计算的输入-输出增益也相对合理，从表1中可以看出，利用积分定义形式计算的输入-输出增益结果对于不同输入信号差别较小。

改变输入的波形，可以得到一系列输入与输出的曲线，如图2所示。本文利用线性函数拟合输入-输出增益，即图中直线。

图2 发电机子系统输入、输出关系Fig.2 Relationship between input and output of generator subsystem

图2（a）中，由于L∞范数定义形式仅能反映信号的幅值信息，对于不同的矩形输入信号，输出的大小基本不变；对于阶跃输入信号，由于干扰持续存在，不同的输入对应的输出也会有所不同，因此，图2（b）中输入、输出分布较为离散。图2（b）中，利用积分定义形式衡量的输入、输出分布均匀，且基本处于同一条直线上。利用线性函数拟合时，分布均匀的数据具有较小的保守性，进一步验证了表1反映的问题。

4.3 电动机子系统输入-输出增益估计

分别利用阶跃、矩形、矩形带冲激信号作为输入，其输入电压有效值和输出电流有效值（标幺值）波形如图3所示，计算得到电动机子系统的输入-输出增益如表2所示。

图3 电动机子系统输入电压和输出电流波形Fig.3 Input voltage and output current waveforms of motor subsystem

表2 电动机子系统输入-输出增益Tab.2 Input-to-output gain of motor subsystem

与表1类似，表2中L∞范数定义形式对于不同矩形以及矩形带冲激的输入信号，利用式（9）计算输入-输出增益时，对于输出的衡量基本相同，不能反映不同输入对于输出的影响，因此用L∞范数衡量输入大小有较大区别时，计算出的输入-输出增益也会有较大差距，见表2中情况Ⅱ—Ⅴ的结果。对于阶跃干扰信号，由于干扰持续存在，利用输出的稳态值可以反映输入信号的部分信息，因此L∞范数定义形式可以适应阶跃输入信号。

改变输入的幅值，可以得到一系列输入与输出的曲线，如图4所示。本文利用线性函数拟合输入-输出增益，即图中直线。

图4 电动机子系统输入、输出关系Fig.4 Relationship between input and output of motor subsystem

图4（a）中，由于L∞范数定义形式仅能反映信号的幅值信息，对于不同的矩形及矩形带冲激的输入信号，输出的大小基本不变；而对于阶跃信号，其计算出的结果基本处于一条直线上，其对于不同输入信号适应性较差，因此计算出的点比较分散。图4（b）中，利用积分定义形式衡量的输入、输出分布均匀，且基本处于同一条直线上，进一步验证了表2反映的问题。

4.4 β函数与α0函数的估计

L∞范数定义形式需要对KL类函数β进行估计，由于函数β与初值和时间相关，增加了估计的难度。若利用指数函数进行拟合，考虑输入电流0.5 kA和1 kA这2种情况，用MATLAB画出仿真结果与拟合曲线见图5、图6。

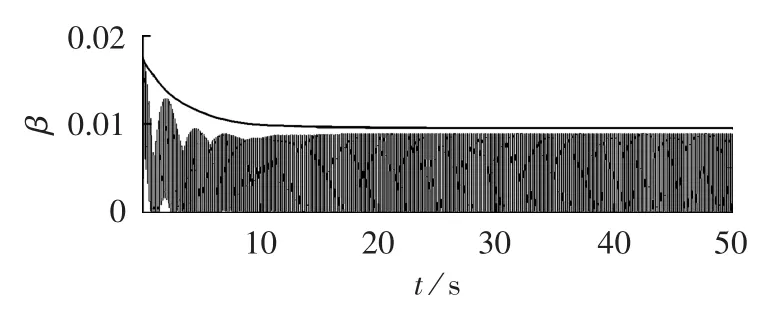
图5 输入电流为0.5 kA时的拟合曲线Fig.5 Fitting curve when input current is 0.5 kA

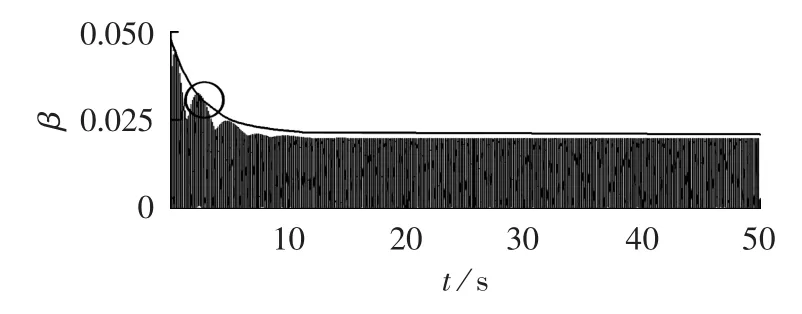
图6 输入电流为1 kA时的拟合曲线Fig.6 Fitting curve when input current is 1 kA

由图5、图6可知，若拟合参数选取不合适，容易出现图6中拟合曲线并未完全包裹实际曲线的情况，使得ISS定义式无法满足。

而采用积分形式，需要估计K∞类函数α0，仅与初值相关，与L∞范数定义形式相比估计难度大幅降低。以发电机子系统为例，α0估计曲线见图7。

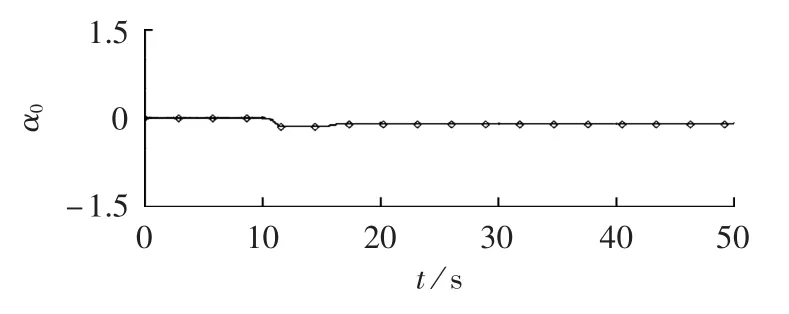
图7 α0的仿真曲线Fig.7 Simulative curve of α0function

只需要取最大值进行估计即可，不会出现L∞范数形式定义中估计曲线无法包裹实际曲线的情况，因此利用积分-积分估计更便捷。

4.5 输入范围的估计

ISS理论另一个关键内容是求解子系统容许的输入范围。对于L∞范数定义形式，利用无穷范数衡量输入信号的大小；积分-积分定义形式则利用积分衡量输入信号的大小。下面以发电机子系统为例，分别用2种定义形式对输入范围进行估计。

对于L∞范数定义形式，利用阶跃信号作为输入，改变输入干扰电流幅值（1～2 kA），当输入干扰电流幅值为1.9 kA时，系统功率出现振荡，频率异常，因此输入范围‖u‖≈1.8 kA。

对于积分定义形式，积分上限值如下：

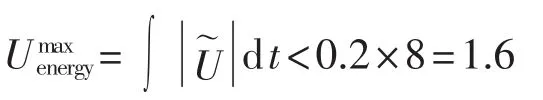
当系统输出积分能量超过极限能量时，认为保护装置动作，即系统不能稳定运行。

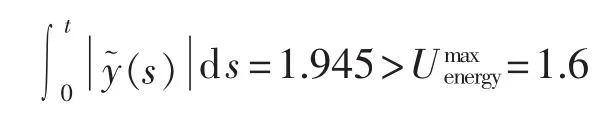
虽然2种方法均可求解系统的输入范围，但L∞范数定义形式利用无穷范数衡量输入大小，因此仅能反映输入信号幅值的信息，而不能反映干扰持续时间内输入信号整体的影响。换言之，对于L∞范数定义形式，只要输入信号的幅值相同，就认为其对于系统的影响是相同的，这显然是不符合实际系统情况的。因此，有必要引入积分-积分估计，对于干扰信号的度量有一个合理的表达。

综上可以得出L∞范数定义形式具有以下几点不足：

a.采用L∞范数度量输入信号，仅能反映其幅值信息；

b.与初值有关的函数β∈KL，是双变量函数，与初值和时间有关，不易拟合；

c.从图2、图4可以看出，L∞范数定义形式的输入与输出的关系和积分定义形式相比较为分散，对于不同类型的输入信号适应性较差，以其上界作为增益函数，将带来较大保守性。

积分定义形式基本弥补了L∞范数定义形式的不足，对于不同类型输入信号有较强的适应性，具有易于估计和保守性较小的优点。

5 结论与展望

本文结合电力设备保护的反时限特性，提出了以稳态运行区间为参考的ISS等价形式，即积分-积分估计，该定义可以避免平衡点变化导致积分趋于无穷的问题，也使得子系统的ISS分析不依赖于互联系统的具体形式决定的平衡点，因此，更符合ISS理论的初衷。进一步，本文给出了一种基于仿真近似估计子系统增益函数的方法，该方法避免了建立微分方程数学模型及参数辨识等困难，且便于考虑实际设备中的限幅、保护等非线性环节。最后，根据实际工程中的干扰类型，选取了4种典型的信号组成干扰集，通过对发电机以及电动机子系统进行仿真，比较L∞范数定义形式与积分-积分估计。仿真结果表明积分-积分估计对于不同的输入具有较好的适应性，并且其增益函数γ和α0均为K∞类函数，估计难度较低，效果优于L∞范数定义形式的估计。

需要指出，本文对于K∞类增益函数均利用线性函数进行拟合，如何改变增益函数估计的形式以进一步降低估计保守性有待进一步研究。此外，为了将以稳定运行区间为参考的积分-积分估计形式应用于工程系统稳定分析，还需研究相应形式的互联系统稳定定理，以便发挥其应用价值。