故障系统低频振荡特征值分析方法

马 静,彭明法,王 形,杨奇逊

（华北电力大学 新能源电力系统国家重点实验室,北京 102206）

0 引言

在故障切除后，由于电力系统的时变和非线性因素显著增强，传统的低频振荡分析方法很难准确反映事故后特征值的变化情况[1-2]。因此，如何从故障系统中提取时变非线性的振荡特性是亟待解决的难题[3-4]。

平衡点特征值法可以描述定长线性系统的全局动态行为，并且可以定量解释低频振荡的机理[5-6]，但是随着系统规模的日益扩大以及结构日趋复杂，利用平衡点特征值法反映系统的振荡特性愈加困难。特别是系统在强时变、强非线性运行条件下，利用平衡点特征值法很可能得到完全错误的结论。为此，众多专家和学者提出了与受扰轨迹密切相关的轨迹特征值法。有别于平衡点特征值法，轨迹特征值法沿着实际受扰轨迹，在不同时间窗口中获取振荡频率和阻尼系数的时间序列[7]。轨迹特征值的时间序列可以反映时变非线性系统在指定扰动下被激发的振荡模式及其随时间的变化情况[8]。但轨迹特征值法的研究主要集中于确定性扰动场景，对于系统在故障类随机因素下（如故障持续时间和故障位置），特征值变化情况的研究则相对较少。且该方法对于窗口宽度的选取依赖性较强，当窗口过宽时，将会掩盖系统的时变振荡特性，而过窄则将会大幅度增加计算量。

本文将平衡点特征值法与轨迹特征值法相结合，提出了一种适用于分析故障系统低频振荡特征值的模型轨迹法。首先，利用共享因子将故障后的系统进行等值，再利用原网络支路电流和故障分量网络支路电流，求取故障后各支路电流以及功率，在此基础上，建立系统的模型并在各测点处分段线性化，将分段线性化模型与系统的受扰轨迹相结合，求解系统特征值的时间序列。最后，利用2机系统和16机系统，分析故障切除后系统特征值和阻尼比的变化情况，算例验证了该方法的正确性和有效性。

1 故障系统的稳定性分析

1.1 故障模型的等值

电力系统的节点电压方程可描述为[9]：

其中，下标N表示发电机节点；下标M表示联络节点（包含负荷节点）；UN为发电机节点电压；UM为联络节点（包含负荷节点）电压；IN为发电机节点注入电流。

消去联络节点[10]，可得仅包含发电机节点的节点电压方程：

其中，Y′NN=YNN-YNMY-1MMYMN为系统的缩减导纳阵。

由式（2）可得各发电机注入节点的电流。网络支路电流Ib与节点注入电流IN的关系如下：

其中，Y为支路导纳阵；A为节点关联阵；Yn为全网络节点导纳阵；C=YATYn-1为共享因子矩阵。

图1为等值2机系统电路图。在t0时刻，系统联络线1上某点发生三相短路，其中短路点距节点B1的距离占整条线路全长的比例为α。经过短路持续时间tc后将故障线路切除，切除后的网络如图2所示。

图1 2机系统线路图Fig.1 Two-generator system

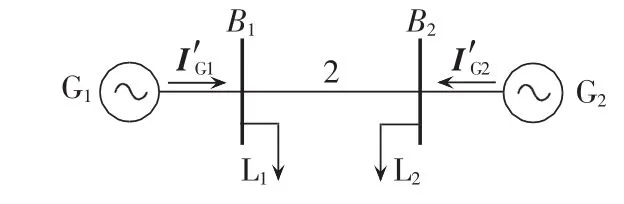
图2 系统故障支路切除后的线路图Fig.2 Two-generator system after faulty line is tripped

设故障前发电机的节点注入电流为IN1，线路切除后发电机的注入电流发生变化，记为IN2。根据叠加原理，线路切除后网络中的潮流分布可以看成由线路切除前的支路潮流和线路切除所引起的故障分量两部分组成，即图2可由图1和图3叠加等值而成[11]。需要注意的是，此时线路切除前的（原）网络注入电流为IN2。

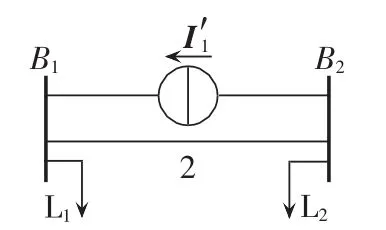
图3 仅含故障分量的等值网络Fig.3 Equivalent system only containing fault components

当节点注入电流为IN2时，由式（3）可知，支路i上的电流为：

其中，I′i为支路 i上的电流；Ci为矩阵 C 的第 i行。

当系统支路i发生故障切除后，系统的故障分量网络仅有一个激励源，即I′i，因此其他线路上的潮流仅与该激励源有关。此时，网络的节点电压方程可写为：

其中，Y′n为故障等值网络的节点导纳阵。

由式（5）可知，该激励源注入各支路的电流为：

其中，I″为故障分量网络中各支路的电流；Y′为该网络的支路导纳阵；A′为节点关联阵；D为共享因子矩阵C=YATYn-1的最后一列。

根据共享因子矩阵，当故障支路切除后，支路k的电流可用下式表示：

其中，Dk为矩阵C第k行的最后一列。

将式（2）代入式（7），可得由发电机节点电压表示的支路电流：

对于图1所示的2机系统，当支路1发生故障切除后，支路2上的电流发生变化，由前面推导可得支路2的电流为：

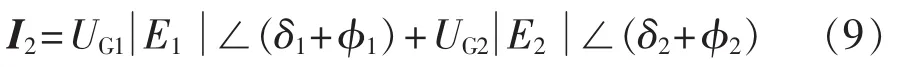
此时，两发电机之间传送的功率可由式（10）表示：

将故障切除后的网络进行等值，通过原网络的节点电压和故障分量网络的支路电流，求取故障切除后网络各支路的电流和功率，以此对系统的特征值进行分析。

1.2 故障系统时变振荡特性分析

以2机系统为例，分析系统在故障切除后的特征值问题，系统的结构如图1所示。引入2机系统经典转子运动方程，并忽略机械功率的变化，则系统经过小扰动线性化后的方程可用下式表示[12]：

其中，δi（i=1，2）为第 i台发电机转子旋转的电角度；ω0为同步速；ωi（i=1，2）为第 i台发电机转子的电角速度；Mi（i=1，2）为第 i台发电机的惯性时间常数；Pei（i=1，2）为第 i台发电机的电磁功率；KDi（i=1，2）为第i台发电机的阻尼系数。

根据功率平衡，发电机输出的电磁功率可表示为[13-14]：

其中，PL1、PL2分别为负荷 L1、L2的有功功率；P12、P21为发电机G1与G2之间的传输功率。

发电机输出的功率经过小扰动线性化后的表达式如下：

将式（13）代入式（11），可得故障线路切除后系统的状态方程：

由式（15）可得，此时系统的状态矩阵A为：

其中，I 为 2×2 维单位阵；k11t、k12t、k22t、KD1t、KD2t分别为 k11、k12、k22、KD1、KD2的时变值。

将系统相应时刻电压的实测值代入式（16），可得该时刻系统的振荡特征值，据此，可得特征值的完整时间序列。

需要注意的是，当系统发生扰动的时候，发电机节点的电压幅值和相角不再是常量，由式（16）可知，系统的状态矩阵A中部分元素也会发生改变，同时，系统的特征值亦发生变化。再者，随着电压幅值和相角变化幅度的增加，特征值的变化幅度也将相应增加。

2 算例分析

2.1 等值2机系统算例仿真

2机系统采用经典二阶模型，系统在0.1 s时联络线1上某点处发生三相短路。故障点距节点1的距离占线路全长的比例为α，经过故障持续时间tc后，将故障线路切除。考虑以下几种故障情况，分析故障系统的时变振荡特性。

a.比例α取0.5，故障持续时间tc为0.05 s。

b.比例α取0.9，故障持续时间tc为0.05 s。

c.比例α取0.5，故障持续时间tc为0.1 s。

d.比例α取0.9，故障持续时间tc为0.1 s。

通过仿真得到系统受扰轨迹后，将相应的实测值代入式（16），计算系统实时特征值的变化情况[15]，如图4—7所示。

由图4和图5可知，当短路持续时间为0.05 s，故障位置改变时两者故障切除后的特征值变化影响较小。其中，精确特征值的实部变化区间为-0.1395～-0.1380，虚部变化区间为3.1～6.7，而利用本文方法计算得到的实部区间为-0.1412～-0.1378，虚部区间为2.5～6.7。由图6和图7可知，当短路持续时间为0.1 s时，此时故障位置改变对故障切除后特征值的影响较大，特征值在实数与复数之间交替变化：当α为0.5时，精确特征值实部区间为-0.14～2.1，虚部区间为0～7，而用本文方法计算得到的实部区间为-0.14～2.2，虚部区间为 0～7；当 α 为 0.9时，精确特征值实部区间为-0.14～3.8，虚部区间为0～7，而用本文方法计算得到的实部区间为-0.14～3.8，虚部区间为0～7，虽然两者的变化区间相近，然而，在同一时刻两者的特征值差异较大。由此可知，不同故障类随机因素对故障切除后的特征值将产生不同影响。一方面，系统在故障切除后，由本文方法计算得到故障切除后的特征值不再是常量，并且变化幅度较为明显。另一方面，系统故障切除后的特征值随着短路持续时间和故障位置的不同，其变化差异较大。

图4 α=0.5、tc=0.05 s时仿真结果Fig.4 Simulative results when α is 0.5 and tcis 0.05 s

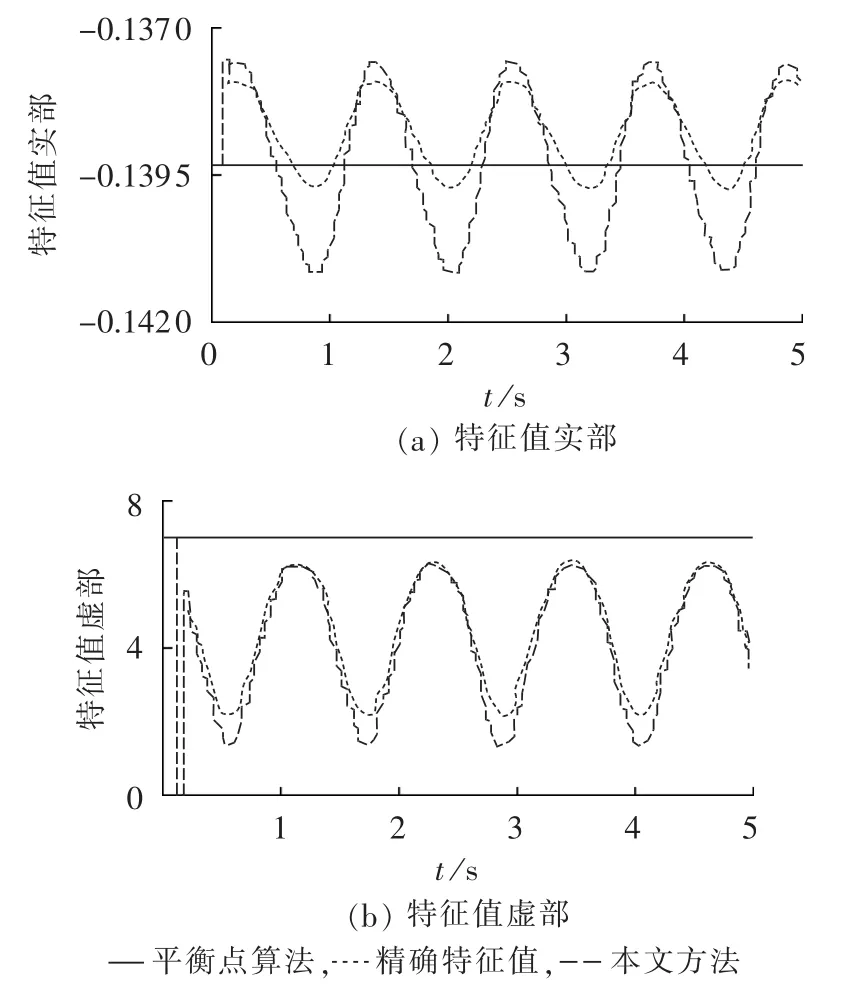
图5 α=0.9、tc=0.05 s时仿真结果Fig.5 Simulative results when α is 0.9 and tcis 0.05 s

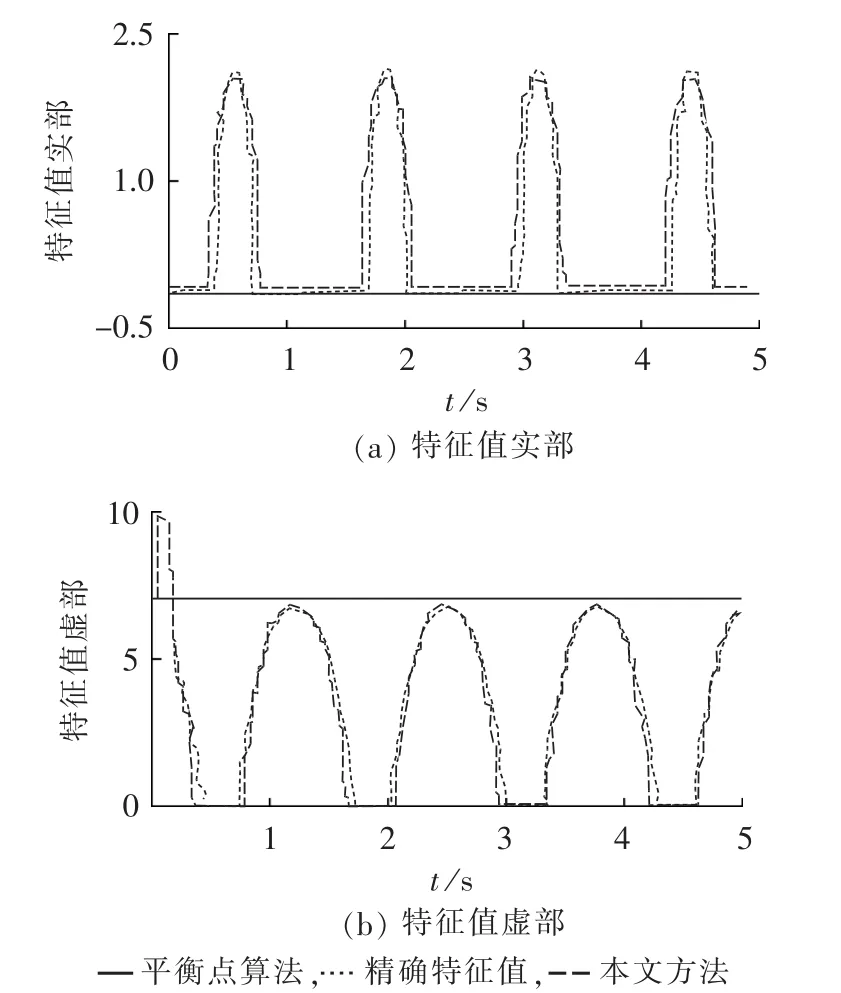
图6 α=0.5、tc=0.1 s时仿真结果Fig.6 Simulative results when α is 0.5 and tcis 0.1 s

图7 α=0.9、tc=0.1 s时仿真结果Fig.7 Simulative results when α is 0.9 and tcis 0.1 s

由图4—7还可以看出，利用本文方法计算得到的特征值能较精确地反映系统实际特征值的变化情况，而利用平衡点算法计算得到的特征值为常数，不能实时反映系统特征值。由平衡点算法计算得到的偏差可由下式表示：

其中，Ri、Mi、ξi分别为利用第 i时刻的实测值计算得到的特征值实部、虚部和阻尼比；R0、M0、ξ0分别为利用平衡点算法得到的特征值的实部、虚部和阻尼比；Rerr、Merr、ξerr分别表示平衡点法与本文方法的偏差；m为实测点个数。

表1给出了4种情况下，利用平衡点法与本文方法计算得到的特征值和阻尼比的相对偏差。由表1可见，短路持续时间越长，利用2种方法计算出的特征值和阻尼比偏差越大，故障位置α越大，两者的偏差也越大。该表同样表明未考虑故障类随机因素的平衡点法不能正确反映故障系统的实时特征值变化情况。

表1 平衡点算法的均方误差Tab.1 Mean square error of equilibrium-point method

2.2 16机系统仿真算例分析

采用IEEE 16机68节点[16-18]的新英格兰—纽约互联系统进一步验证本文方法的正确性和有效性，系统结构如图8所示，该系统可分为五大区域。其中发电机采用六阶详细模型，励磁采用IEEE-DC1型励磁。系统在0.1 s时刻，线路28-29某处发生三相短路故障，故障点距节点28的距离占线路全长的比例为α。分析以下4种故障情况下，故障切除后系统的特征值变化情况。

a.比例α取0.5，故障持续时间tc为0.02 s。

b.比例α取0.9，故障持续时间tc为0.02 s。

c.比例α取0.5，故障持续时间tc为0.05 s。

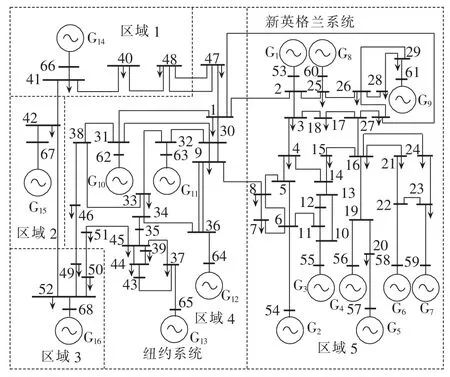
图8 16机68节点电网结构图Fig.8 Structure of 16-generator 68-bus system

d.比例α取0.9，故障持续时间tc为0.05 s。

将系统仿真得到的轨迹代入式（16）中，由此得到特征值的时间序列。其中区域4与区域5之间振荡模式的时间序列如图9—12所示。

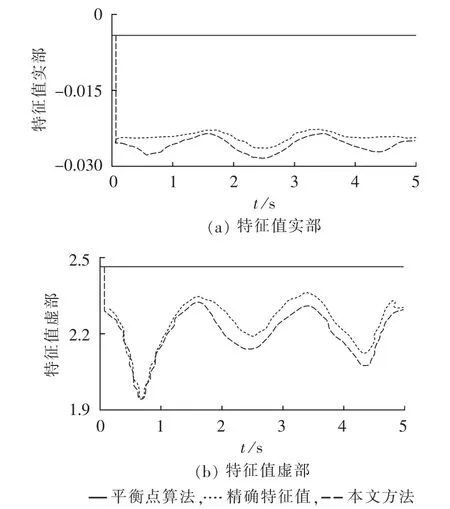
图9 α=0.5、tc=0.02 s时仿真结果Fig.9 Simulative results when α is 0.5 and tcis 0.02 s

图10 α=0.9、tc=0.02 s时仿真结果Fig.10 Simulative results when α is 0.9 and tcis 0.02 s

由图9—12可知，基于本文方法计算得到的特征值亦不再为常量，而是随时间发生相应的变化，且随故障持续时间和故障位置的不同，其变化情况也各异。同时，本文方法能够较精确地跟踪系统的特征值变化。

表2给出了不同短路持续时间和故障位置时，利用平衡点法与本文方法计算得到的特征值和阻尼比的相对偏差。由表2可知，当短路持续时间越长时，利用平衡点法与利用本文方法得到的特征值和阻尼比的偏差越大，这同样也表明平衡点法不能正确反映故障系统的振荡特性。

图11 α=0.5、tc=0.05 s时仿真结果Fig.11 Simulative results when α is 0.5 and tcis 0.05 s

图12 α=0.9、tc=0.05 s时仿真结果Fig.12 Simulative results when α is 0.9 and tcis 0.05 s

表2 平衡点算法的均方误差Tab.2 Mean square error of equilibrium-point method

3 结论

本文提出了一种分析故障切除后系统低频特征值的方法，即模型轨迹法，该方法首先将故障切除后的系统进行等值，再利用原网络支路电流和故障分量网络支路电流，求取故障后各支路电流以及功率，在此基础上，建立等值系统的运动方程，并在各测点处将等值模型分段线性化，结合实际受扰轨迹，求解系统特征值的时间序列。最后，利用2机系统和16机系统，分析故障类随机因素对系统振荡特性的影响，算例结果验证了该方法较平衡点特征值法，能够更准确地跟踪系统特征值的变化情况，同时，也有效避免了利用轨迹特征根法求解电力系统时变特征值的窗口选取问题。