收网算法及其在低压配电网潮流优化中的应用

2014-09-26刘皓明朱芳芳钱程晨

电力自动化设备 2014年4期

刘皓明,朱芳芳,钱程晨

（河海大学能源与电气学院,江苏南京 211100）

0 引言

配电网的潮流优化是保证其安全、经济运行的有效技术，同时也是提高配电网电压质量的重要方法之一。本文以有载调压变压器OLTC（On-Load Tap Changer）、无功补偿器、可控分布式电源和插电式混合动力汽车PHEV（Plug-in Hybrid Electric Vehicle）作为控制设备，将现代配电网网损最小作为主要目标建立了优化模型，并考虑系统各节点各相电压的限制，对现代配电网进行潮流优化分析计算[1]。

针对配电网的潮流优化，目前已提出一些解决方法。典型的传统优化法有线性规划法[2]、非线性规划法[3]和混合整数规划法[4]，当初始解在最优解附近时，这些方法通常具有良好的寻优能力，但此类方法对系统目标函数及约束条件的连续性、可微性等方面有较高要求。而现代启发式智能优化算法，如遗传算法[5-6]、粒子群算法[7-8]等，以一组初始解代替一个初始解进行寻优，对目标函数及约束条件的要求比较低，能够较为方便地解决不可微、不连续等传统优化方法不能处理的问题，已成功应用于电力系统无功设备优化配置[7]、经济负荷分配[8]等。通过精心选取启发式智能优化算法参数，可以获得较高的优化性能。

本文以网损最小和电压分布合理为目标，建立了现代低压配电网优化模型，并提出了一种新颖的模拟渔民收网捕鱼的启发式智能优化算法：收网算法SNA（Shrinking Net Algorithm）。该算法从搜索空间边界出发，逐步向空间内部进行压缩搜索，需要设置的参数少，全局收敛性强，寻优效果好。本文从数学上证明了其具有良好的收敛性，并将其用于三相不对称的现代低压配电网优化问题，取得较理想的优化结果。

1 现代低压配电网潮流优化模型

传统低压配电网一般只包含2种节点：平衡节点和PQ节点。而随着配电网的发展，多种分布式电源和新型负荷的增加，低压配电网中增加了其他类型的节点。同时低压配电网还存在着三相线路阻抗不对称、负荷三相不平衡、阻抗比较大等因素。

本文优化模型以网损最小和节点电压优化分布为目标，将节点电压越限作为惩罚项计入目标函数。计及潮流等式约束、并联电容无功补偿约束、变压器变比调节范围约束、可控分布式电源出力约束和PHEV充电功率约束，建立优化模型如下：

其中，Zij（k）和 Iij（k）分别为支路 ij第 k 相阻抗和流过的电流，k∈｛A，B，C｝；j∈i表示下游节点 j与上游节点 i间存在支路直接相连；λ为惩罚系数，可取一较大正数；Ui（k）和 Uj（k）分别为节点 i和 j第 k 相电压；ΔUi（k）、Umaxi（k）和 Umini（k）分别为节点 i第 k 相的电压越限量和电压上、下限；Qc（k）、Tt（k）、Pg（k）和 Pp（k）分别为第 k 相第 c个无功补偿装置无功补偿量、第t个变压器分接头位置、第g个分布式电源的出力和第p个PHEV充电功率；Qmaxc（k）和 Qminc（k）、Tmaxt（k）和 Tmint（k）、Pmaxg（k）和 Pming（k）、Pmaxp（k）和 Pminp（k）分别为各自的上、下限；NB、NC、NT、NG和 NP分别为系统节点数以及无功补偿装置、变压器、分布式电源和PHEV接入的节点数。

其中，Ij（k）为节点 j第 k 相负荷电流。

2 现代低压配电网潮流计算方法

本文引入一种改进前推回代算法，对含弱环的现代配电网进行开环点功率补偿迭代计算，使之能够计算含新型分布式电源的配电网三相不对称潮流[10]。

2.1 负荷模型

2.1.1 一般负荷

负荷一般可以等效成3类：恒功率（PQ）、恒电流（I）和恒阻抗（Z）。

2.1.2 分布式电源

分布式电源的种类较多，根据其接入配电网后所表现出来的特性，可以作以下分类[11]：微型燃气轮机、燃料电池等可控分布式电源为PV型节点；光伏、储能为I型节点；工频热电联产异步机组为有功恒定而无功随着节点电压变化而变化的PQ（V）型节点；工频热电联产同步机组等为PQ型节点。

对于I型节点和PQ型节点，直接转换为节点注入电流进行前推回代算法计算。而对于PV型节点，需要对前推回代法作相应改进。

2.1.3 PHEV

PHEV通常从电网吸收恒定的充电有功功率，在特殊条件下也可服从电网调度，充电功率大小可变甚至向电网释放电能。本文将其视为PQ型节点，并从研究的角度出发，假设其充放电功率可控[12]。

2.2 环网和PV型节点处理

传统前推回代法无法直接处理PV型节点和环网，因此需要对其解环[13]。

假设配电网中存在nl个环网和nPV个PV型节点（与大电网相连的根节点除外），将环网和PV型节点（后文统称为环网）都解开至纯辐射状，则有nl+nPV个开环点，有：

其中，Z=R+jX为环网阻抗，R和X分别为环路电阻和环路电抗；I为环路注入电流；ΔU为开环点两侧电压差。

假定相邻节点的电压幅值差较小，并且都接近1 p.u.，同时相角相差很小，则有：

推导得：

其中，S为环路注入视在功率；ΔP和ΔQ分别为开环点补偿的有功功率和无功功率；ΔU′和δU分别为开环点电压差的横分量和纵分量，ΔU=ΔU′+jδU。

在求解含PV型节点和环网的配电系统潮流时，先计算解环后的潮流，得到开环点电压差，然后根据式（11）计算该点补偿功率。下一次迭代计算潮流时在该开环点加上补偿功率，重复计算，直至开环点的电压差满足收敛条件。

2.3 潮流计算流程

潮流计算流程如下。

a.读取配电网数据，形成节点支路关联矩阵。

b.判断环网和PV节点，对其解环重新生成网络矩阵。

c.初始化电压。

d.计算末梢节点注入电流，对于I型节点直接叠加，其他几种类型的节点转换成恒功率节点，等同于PQ型节点进行处理。

e.根据式（7）前推计算各支路电流。

f.根据式（2）回代求解各节点电压。

g.计算开环点 ΔU′和 δU，由式（11）计算补偿功率ΔP和ΔQ，并叠加到相应的节点上。

h.检查所有开环点电压是否满足收敛条件，若满足，则停止计算，输出结果；否则，返回步骤d继续进行迭代计算。

3 收网算法

为求解本文建立的优化模型，提出了一种收网算法。它是一种从变量空间的边界出发，向着全局最优解方向进行压缩式搜索的优化方法。

3.1 术语

维数：优化变量的个数，用D表示。

结点：一个可行解，记为 Xi=[Xi1，Xi2，…，XiD]，Xid表示第i个结点的第 d维分量，d=1，2，…，D。

顶点：一类特殊的结点，由各维变量上、下限的组合所构成，对于D维搜索空间，顶点中包含的结点数为2D个。

网面：所有初始化结点构成的集合，由顶点和在每一维上、下限处超平面所围成的边界面上选取的若干个随机结点构成，若每个处于边界的超平面均取N个随机结点，那么网面中包含的结点个数为P＝2D+2ND。

最优结点：当前迭代中出现的一个最优解。

收拢：群体的一次更新迭代操作。

开拓系数：收拢操作中影响群体变化的一个关键系数。

越界：一个结点的某一维在更新变化过程中超出其自身的上、下限。

3.2 基本流程

收网算法基本流程如下。

b.将网面上的各个结点代入目标函数进行计算，得到当前全局最优解Xbest。

c.收拢。对各结点按下式进行更新计算：

其中，i=1，2，…，P；m=1，2，…，M-1；P 为网面结点总数；M为最大迭代次数；Xi（m）为第m轮迭代中的第i个结点；Xbest为当前最优结点；C为开拓系数，其取值大小影响收网算法的全局和局部寻优能力；分别为[0，1]之间均匀分布的随机向量。

d.越界判断。若某次迭代更新后某些维超出自身的上、下限，则对其进行限值。

e.返回流程b，直至m=M-1，输出优化结果。

由于每一轮的最优结点经过式（12）计算以后依然是其本身，因此只有在出现更优的结点时，此前的“最优结点”才会被更新，这一点保证了群体的非劣性。

3.3 收敛性分析

将式（12）进行整理，得：

假设在迭代过程中，Xbest不变，对式（13）进行分析，并令：

陆徵祥八任外交总长，两任国务总理，在此期间签订了令他痛心的《二十一条》，拒绝了巴黎会议上政府施压让他在《凡尔赛和约》上签字的要求。他在任期间为中国外交的现代化做出了贡献，创建了外交人才的培养体系。

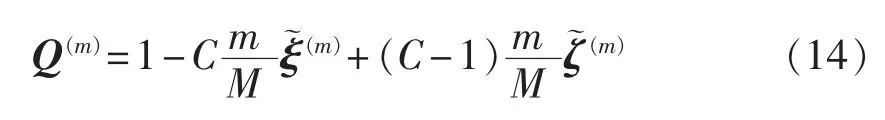
有：

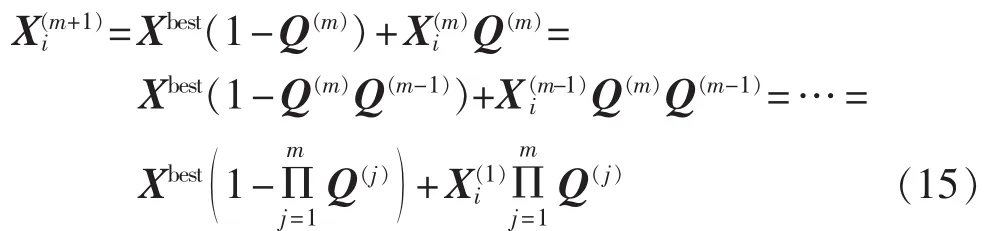
其中，Q（m）为当前结点在最近2次迭代中与最优个体间距离的比值。若，表示随着迭代的进行，当前结点与最优结点的距离越来越远；若，则表示当前结点与最优结点之间的距离越来越近。

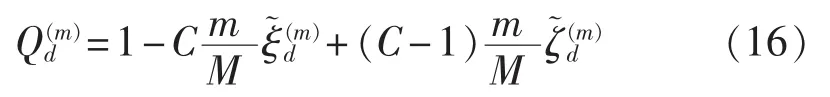
Qd（m）期望值为 0.75，说明网面上的各结点在期望上越来越靠近最优结点。实际上，Qd（m）取值与2个随机数以及开拓系数C的取值大小相关，合适的开拓系数能够加速收网算法的收敛。

3.4 开拓系数的选取

开拓系数C是收网算法唯一需要设置的参数，其值影响 Qd（m）的大小，根据式（16），有：

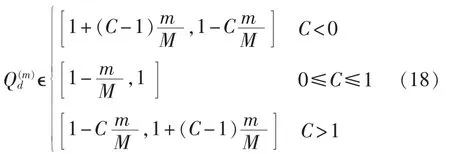
当 0≤C≤1 时，Qd（m）处于（0，1]之间，表明 X（im+1）是在同一个方向上逐渐逼近于Xbest的，反映了收敛算法的局部收敛能力；当C不在这个范围内时，Qd（m）的取值范围比较大，有可能出现小于0或大于1的情况，此时，反映了收网算法的全局寻优能力。

进一步分析最后若干轮的迭代情况。当m足够大，且 C∈[0，1]时，Qd（m）∈（0，1]，由于都是在[0，1]上相互独立且均匀分布的随机变量，那么可认为Q（dm）在其取值范围内也是均匀分布的。假设最后的若干轮迭代 Xbest不再发生变化，若用代替 Q（j），则：

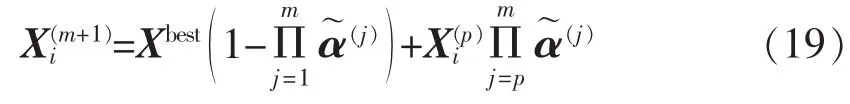
由上述分析可以给出开拓系数C的选取原则：在前期迭代过程中设置较大值，例如C>1，以适当提高其全局寻优能力；在后期迭代中，设置为C∈[0，1]，以保证算法的局部收敛效果。

3.5 算法性能测试

为验证分析结果，选取典型的测试优化方法全局搜索性能的“Generalized Schwefel’s Problem”函数，函数表达式如下：

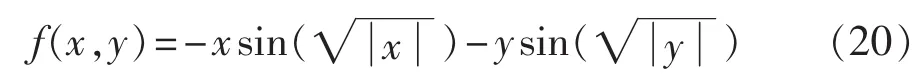
其中，x、y∈[-500，500]。测试函数搜索空间如图 1所示。

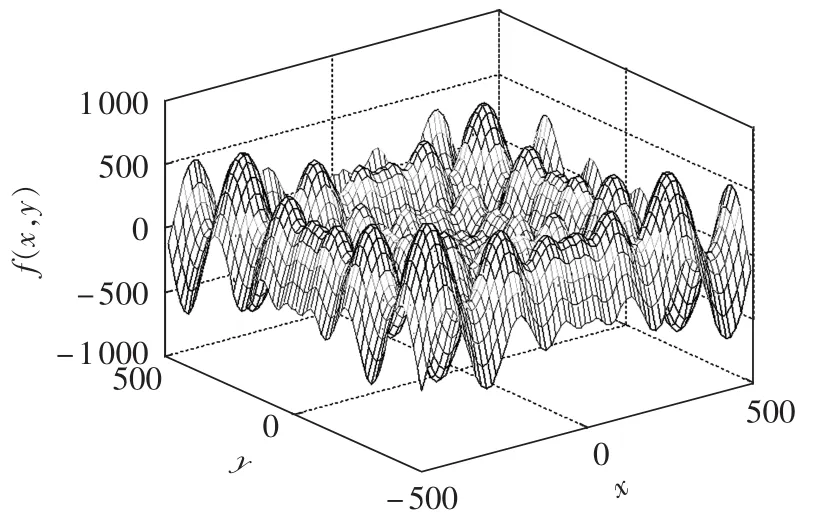
图1 测试函数搜索空间Fig.1 Search space of test function

使用收网算法与标准粒子群算法分别运行200次作对比测试，设置最大迭代次数M=50。在收网算法中，2维空间共有4个超平面（四边形共有4条边，见图1）和4个顶点，在每个超平面上随机选择N=10个结点，则初始结点规模P=2D+2ND=22+2×10×2=44，设置4种定开拓系数和1种变开拓系数C＝f（m）=20-19.5 m/M情形；在粒子群算法中，同样取群体规模为 44，惯性权重 ω 取值范围[0.5，1.4]，c1=c2=2[14]。2种算法的对比结果如表1所示，其中粒子群算法仅列出收敛成功率最高的情况，此时惯性权重系数为ω=0.7。

表1 优化结果统计Tab.1 Statistics of optimization results

由表1可以得出以下结论。

a.收网算法与粒子群算法均具备全局最优搜索能力，也会出现一定概率的陷入局部最优的情形。

b.从整体上看，收网算法的全局寻优能力更强，且稳定性好、精度高。

c.当开拓系数为常数且小于1时，各个结点处于严格逼近于当前最优结点的过程中，因此损失了一定的全局寻优能力；随着开拓系数的增大，全局寻优能力得到显著的提高，当开拓系数选取过大时，会导致在搜索后期寻优精度降低，甚至会出现各结点在寻优过程中处于发散状态的情况，反而降低了寻优成功率。

d.选取随着迭代次数自适应变化的开拓系数C，既能使收网算法具有很高的全局寻优能力，又能保持较高的寻优精度，以此验证了3.4节中开拓系数C的选取原则。

4 算例分析

本文选择IEEE 123节点配电系统为算例[15]，网络拓扑如图2所示。在原系统8个节点上分别添加了若干可控分布式电源和PHEV，本算例仅将PHEV作为普通可控负荷。此外，系统中还包含2类可控装置：有载调压变压器和无功补偿装置（Cap），具体参数如表2所示。计算中假设各节点各相电压上、下限分别为1.05 p.u.和0.95 p.u.。

图2 IEEE 123节点系统Fig.2 IEEE 123-bus system

利用本文建立的优化模型和提出的收网算法进行优化计算。设置最大迭代次数M=50，选取开拓系数C＝f（m）=20-19.5m/M。对应14个可控设备，每个边界随机选择2个结点，则初始结点规模P=2D+2ND=214+2×2×14=16440，计算量很大。采用本文提出的降低初始结点规模的方法，忽略所有顶点，则初始结点规模为56。收网算法收敛曲线见图3。

该123节点系统满负荷状态运行时，系统有功网损为96.103 kW，且各节点电压偏低，平均电压为0.969 p.u.，节点104的C相电压最低，为 0.937 p.u.。经过优化后，系统有功网损为65.208 kW，节点电压分布更合理，所有节点均满足电压上、下限限制，平均电压为1.017 p.u.，节点114的A相电压最低，为0.973 p.u.。优化后的各可控量优化结果见表2。

优化后节点90无功补偿为0 kvar，这是因为在该节点注入无功会造成有功网损的增加，同时经计算发现，当节点90的50 kvar无功补偿全部投入后，多个节点电压越限。