竖通道内液体燃料燃烧形成的旋转火焰特性

霍 岩，邹高万，李树声，郜 冶

（哈尔滨工程大学航天与建筑工程学院，150001哈尔滨）

火焰周围流场等压面与等密度面斜交引起的旋转火焰［1］，作为一种特殊的火焰形态，可发生于各类竖井通道、高层建筑玻璃幕墙、高大中庭空间、甚至房间室内火灾中，一般由切向气流被高温低压的火焰从通道壁面侧开缝处引入产生.一旦建筑火灾中形成了旋转火焰，更快的燃烧速度和更高的火焰高度会加剧火势的蔓延，提高对建筑结构和人员生命安全的威胁程度，并加大火灾的扑救难度.对于发生在森林和城市中的外界大型火旋风，已有很多相关研究工作完成［2-6］，但对于有限开口空间内自然对流形成的火旋风，由于空间尺寸和壁面，以及开口通风情况都会对旋转火焰的生成、维持和溃灭过程产生影响［7］，因此较外界的大型或强制火旋风不尽相同.由于缺少实验和测量数据，目前对有限开口空间内的旋转火焰热流场还未有成型理论.本文利用实验与基于大涡模拟技术的数值模拟方法研究在具备形成旋转火焰的竖直通道模型中相对稳定火源所形成的旋转热流场，所得结论对深入理解有限开口空间内旋转火焰特性有一定意义.

1 实验条件设置

顶部开口的方形竖通道实验装置如图1所示，装置由厚0.5cm的木板组成，内部空间尺寸为：长32cm（X）×宽32cm（Y）×高200cm（Z），正面（装置前侧观察方向）镶嵌玻璃，可对通道内实验现象进行观察和图像记录.装置的两侧活动壁面可形成宽度d的侧开缝，在通道底部中心放置盛装液体燃料的圆形油池.实验过程中，通道的侧开缝形式为两侧斜对，即左侧壁面的开缝在靠近前壁面一侧，右侧壁面的开缝在靠近后壁面一侧.通道中心布置一温度测点树，共17个测点，在100 cm高度以下各测点间距10 cm，100 cm以上每个测点间距15 cm.通道装置的侧开缝形式和温度测点布置如图2所示.

图1 竖直通道实验装置照片

为了获得不同的热释放率，实验所用圆形燃料池的直径Φ分别为7.4 cm，8.4 cm和10.0 cm，燃料池边沿均高2.0 cm.实验所用液体燃料为正庚烷（浓度为97%），每实验条次的燃料使用量为25 mL.实验过程中使用美国 Ioteeh公司的DaqBook2005数据采集系统进行流场温度数据的测量与记录，数据采集和记录时间间隔为0.5 s.实验过程中，环境温度保持在21～22℃，近处门窗和机械通风等全部被关闭，以防止对通道内流场造成干扰.

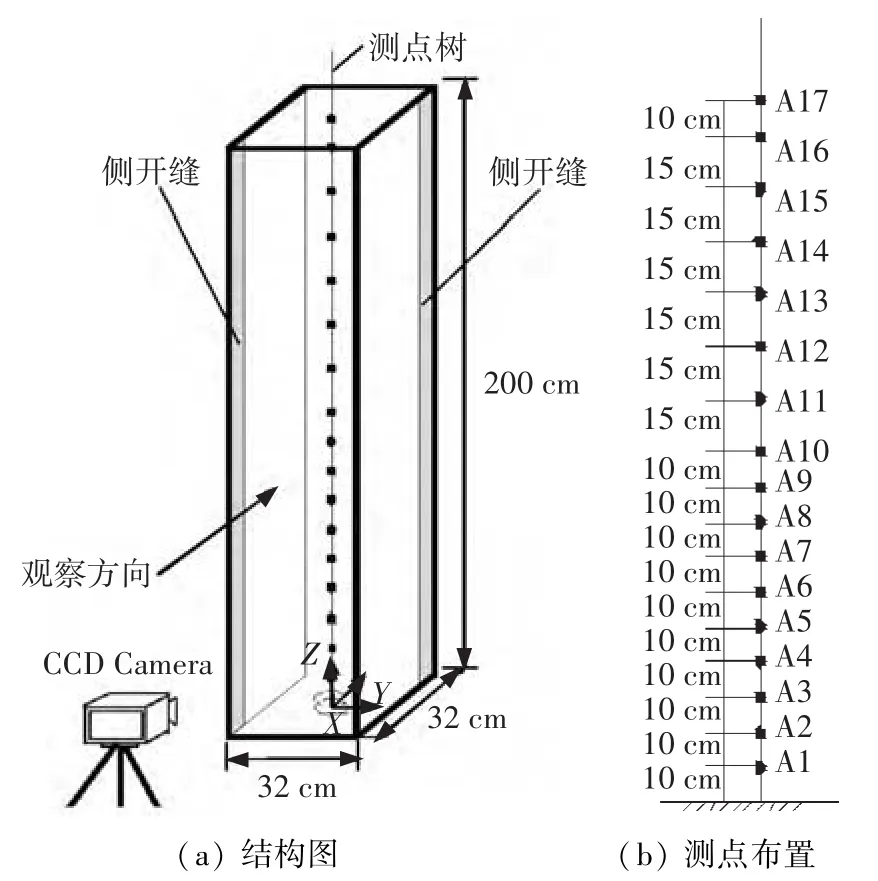
图2 竖直通道结构与内测点布置

2 数学物理模型

由通道侧开缝引射空气所形成的非受迫旋转火焰流场基本动力学方程组、为加快计算速度和结果收敛所进行的公式简化变形等在文献［8-9］中已有详细的推导，在此不再赘述，仅简要介绍相关重要源项的计算方法和主要参数取值.

数值计算时将燃烧简化为单步不可逆的简单化学反应，采用混合分数燃烧模型，可燃物燃烧消耗单位质量氧气所释放的能量值取 1.31×106J／kg［10］.决定液体燃料燃烧速度的燃料池表面蒸汽压力由Clausius-Clapeyron 公式［8，11］来限制式中：R为气体常数；Tcc为液体燃料表面温度；ΔHv为液体燃料的汽化热，对于实验所使用的正庚烷燃料，取值 4.8×105J／kg；Tboil为燃料沸点温度，取值98.4℃；p0为大气压力，取值101.325 kPa.

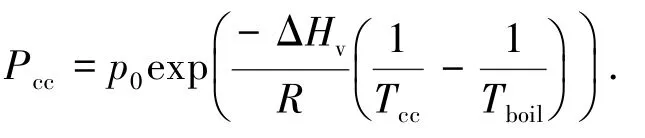
另外，根据实验中所使用正庚烷燃料属性，取密度值为680 kg／m3，比热容为2 200 J／（kg·K）［12］，导热系数 0.14 W／（m·K），液面厚度 1.5 cm.燃料液面以下的热传导过程使用一维导热模型来计算.

湍流模型采用基于Smagorinsky亚格子的大涡模拟（LES）模型；流场中的辐射热传递采用有限体积法来求解；边界层速度与粘性应力由基于Werne与Wengle边界层模型［13］来计算；通道装置壁面导热使用一维导热模型来计算，根据实验竖直通道装置的外边界材料，在计算过程中，装置的木板壁面参数设置为：密度545 kg／m3；比热容1 210 J／（kg·K）；导热系数 0.14 W／（m·K）.装置前侧玻璃参数设置为：密度2 700 kg／m3；导热系数 0.76 W／（m·K）；比热容 840 J／（kg·K）.

数值计算过程中，各空间变量采用二阶有限差分法离散，时间的微分项则以显性二阶Runge-Kutta法离散化.为了保证求解过程的稳定性，使用CFL稳定限制条件对迭代过程的时间步长进行调整.

3 结果与分析

图3～5分别为燃料池直径Φ为7.4 cm，8.4 cm和10.0 cm时的通道内流场达到稳定后，通道内中心轴线上高度Z处的温度T实验（Expt）与数值模拟（CFD）结果对比，其中实验结果为各测点温度记录值在流场稳定阶段的算术平均值.图中对实验与数值模拟结果使用Euclidean函数分析法［14］对进行量化分析，其norm与cosine的值分别表示模拟结果与实验结果的偏差和变化相似程度，计算公式为

式中：E和m分别为实验值和模拟值，i表示第i个离散点．

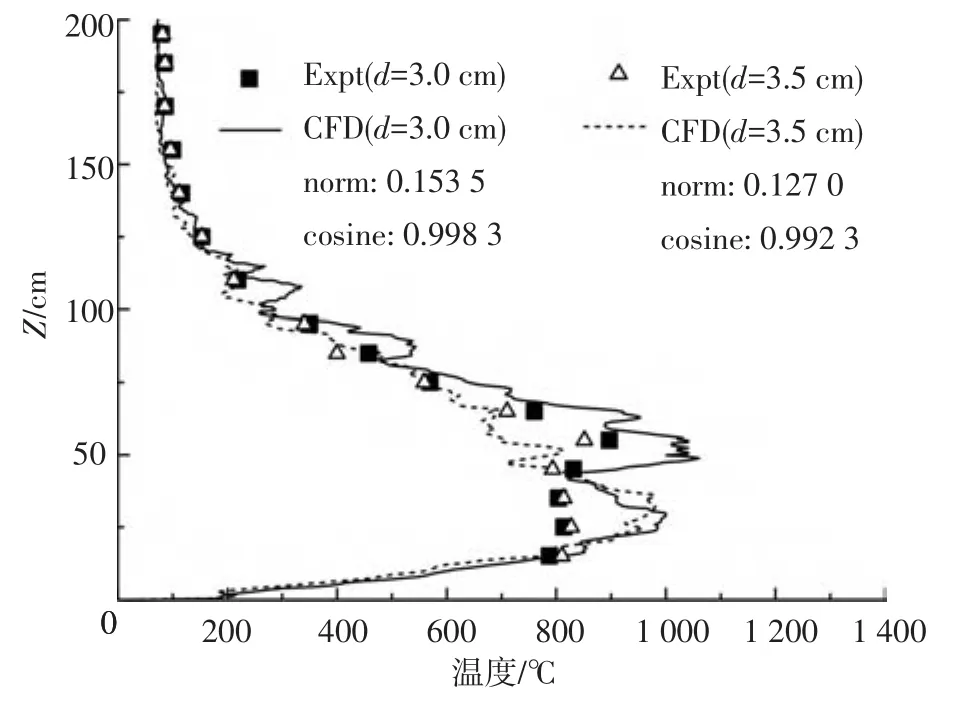
图3 中心轴线上温度实验值与模拟值比较（Φ7.4 cm）

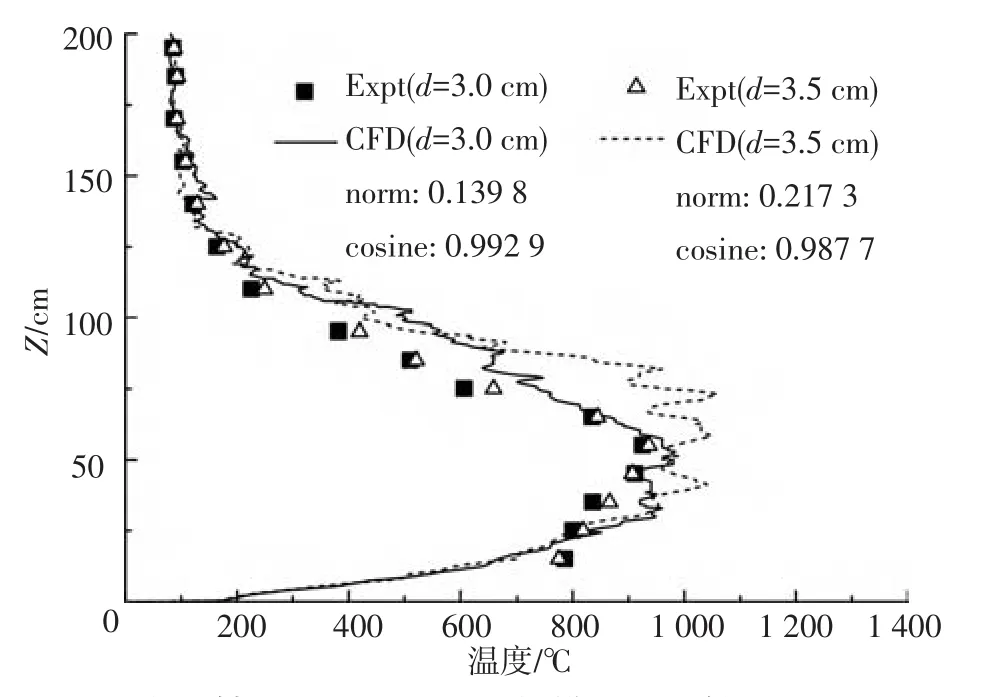
图4 中心轴线上温度实验值与模拟值比较（Φ8.4 cm）

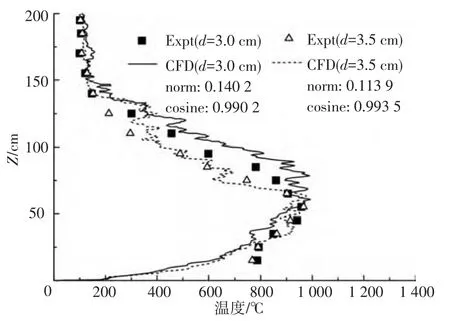
图5 中心轴线上温度实验值与模拟值比较（Φ10 cm）

由图3～5中可以看出，模拟结果与实验结果的纵向温度整体分布规律十分相似，偏差稍大的区域主要在通道中下部，这是由于火焰所在区域的复杂特性造成的.但通过函数分析法得到的结果可以看出模拟结果与实验结果在整体上符合较好，偏差在可接受的范围内.

图6为相同火源在通道外自由燃烧和在通道内形成旋转时的热释放速率HRR随时间t变化的模拟结果对比，可以看出，形成旋转火焰后的热释放速率较自由燃烧时增加2倍多，这符合旋转火焰的特性，说明所采用的模拟方法可以模拟出旋转对液体燃料燃烧的加速作用.

图6 不同环境下火源热释放速率的模拟结果

图7为开缝宽度d为3.5 cm时，燃料池直径Φ分别为7.4、8.4和10 cm的实验旋转火焰照片与模拟结果对比.由图中可以看出模拟的火焰呈现出类似实验结果的柱状形态，并且具有非常接近的螺旋纹理.这些均表明所采用的数值模拟方法可以较准确地反映通道内旋转火焰热流场.

图7 实验火焰照片（左）与模拟结果（右）比较（d＝3.5 cm）

图8为高度Z分别为60、120和180 cm处，过火源中心所在位置（坐标原点）到通道两侧壁面方向（X轴）的切向速度V变化．由图可以看出，火焰两侧的切向速度变化规律近似对称，并且切向速度值随着高度升高逐渐降低；同一高度处，燃料池直径较大时，在火焰外侧的切向速度值更大；通道两侧壁面附近的切向速度绝对值均保持在100 cm／s左右，在60 cm高度时，由火焰中心向通道两侧壁面方向，切向速度先迅速增大，到达最大值后又逐渐降低到100 cm／s附近，而在120 cm高度以上时，由火焰中心向通道两侧方向，切向速度只是逐渐增大到100 cm／s附近，而没有降低过程.

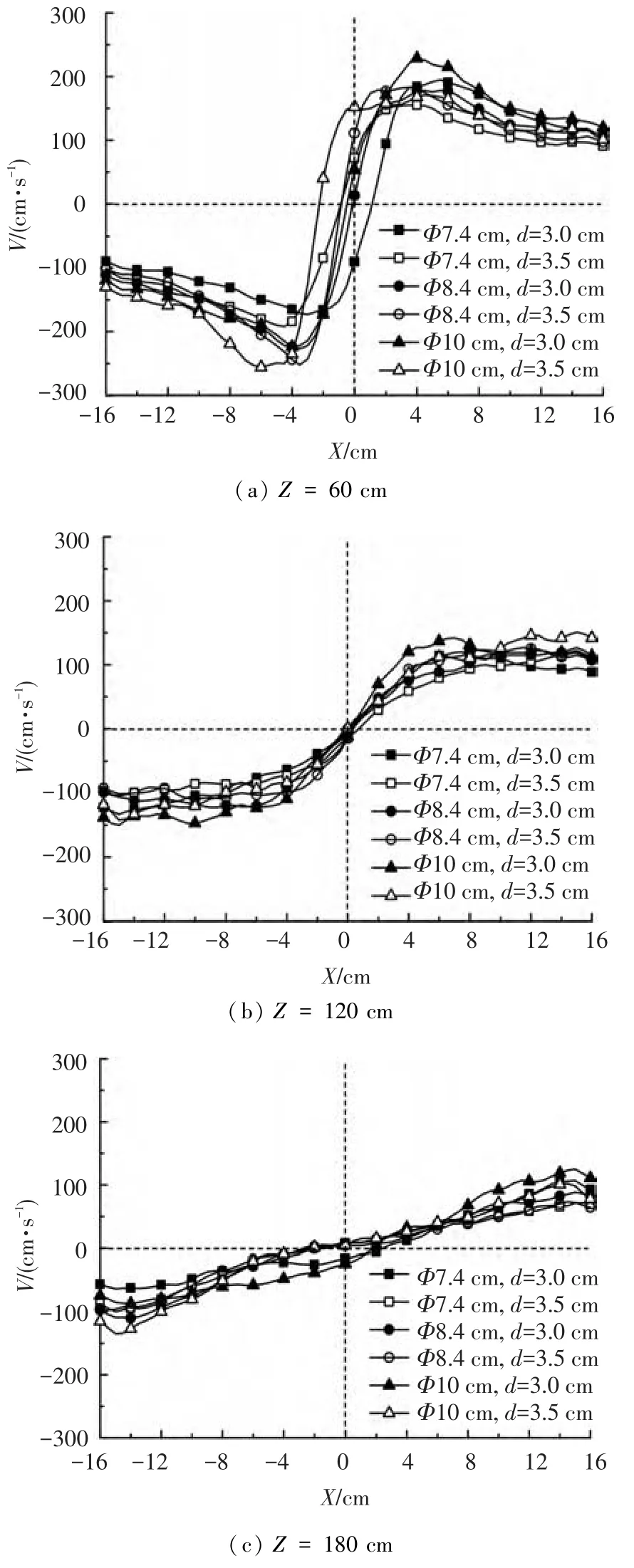
图8 不同高度的X轴上的切向速度变化

与自由燃烧的池火热流场中浮力为主导力不同，旋转火焰热流场会表现出旋转科氏力与热浮力共同作用的复杂特性，为了考察旋转火焰热流场中旋转的科氏力与竖直向上的浮力对流场的作用程度关系，定义无量纲量ζ为科氏力与浮力之比：

式中：ρ为气体的密度；ρ∞为环境密度；V为速度矢量；ωz为角速度矢量；g为重力加速度矢量．

侧开缝宽度d为3.0 cm和3.5 cm时，不同燃料池直径Φ内燃烧形成的旋转火焰在不同高度Z处的无量纲量ζ的值如图9和图10所示．由图中可以看出，在火焰中心，由于切向速度为零，所以ζ为零；由火焰中心向通道两侧方向，ζ值变化规律近似呈现对称分布，均是先逐渐增大，而后又逐渐降低，最大ζ值发生在火焰外侧位置．同时随着高度增加，ζ值逐渐降低，这说明相比浮力，旋转科氏力对流场的作用随着高度的增加而减弱．另外，高度1 m以下的通道下半部分，通道中心两侧的ζ值大于1，而通道上半部分的ζ值小于1，这说明在通道下半部分科氏力对流场的影响较浮力大，而在通道的上部分，浮力则对流场起主要作用．

图11为不同燃料池直径Φ对应火源所形成的旋转火焰热流场中最大轴向速度Wmax与最大切向速度Vmax之比的无量纲模拟结果与实验数据计算结果，实验结果按文献［15］的计算方法：

式中，z3和z2分别为火焰区域Ⅲ与火焰区域Ⅱ的高度［15］．由图11可见，数值模拟结果与实验计算结果很接近，两者吻合程度较好，并且通道旋转火焰热流场中的最大轴向速度约为最大切向速度的2倍．

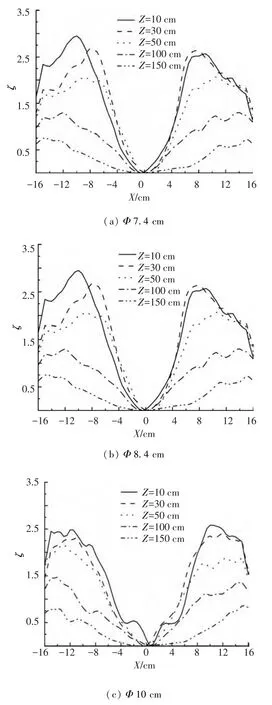
图9 不同高度的科氏力与浮力之比（d＝3.0 cm）

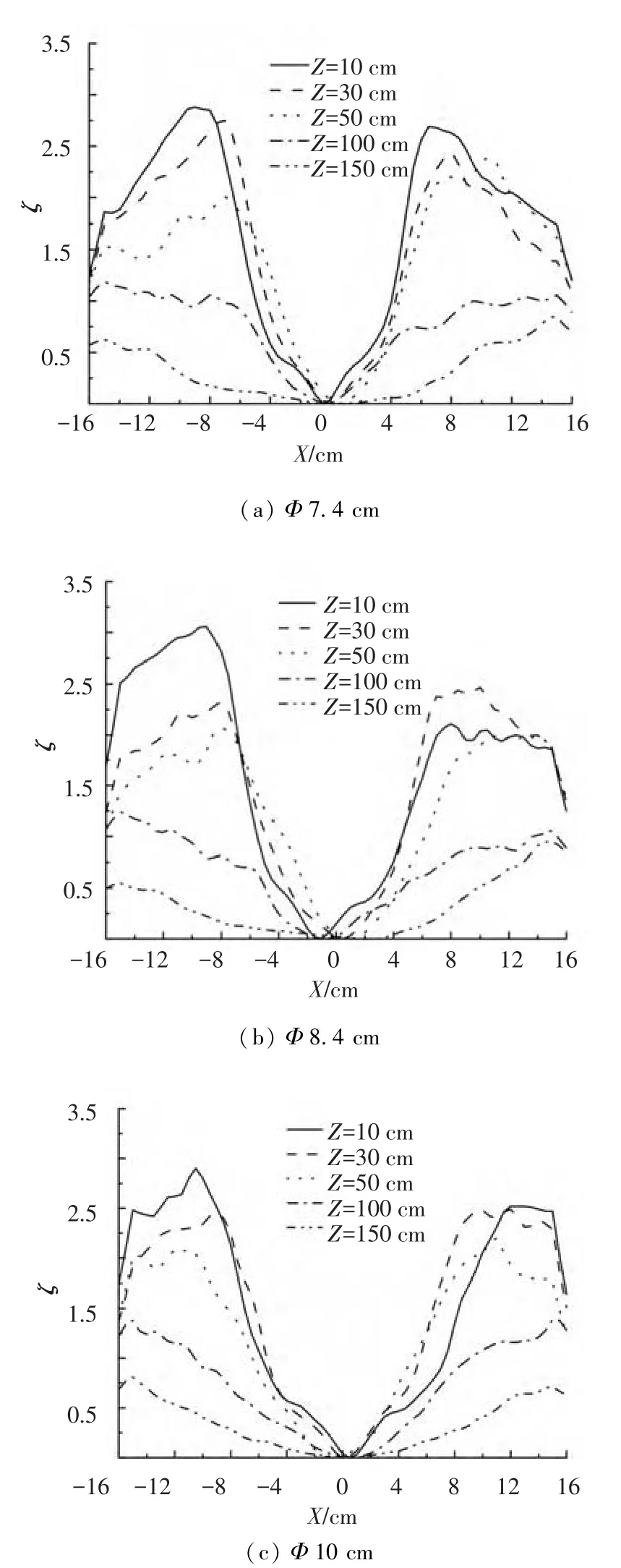
图10 不同高度的科氏力与浮力之比（d＝3.5 cm）

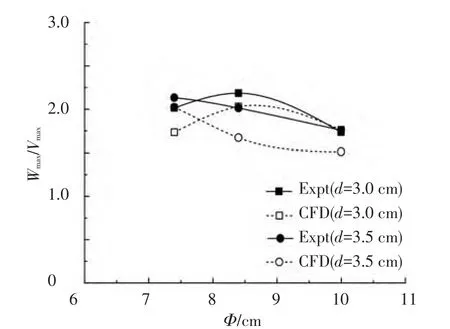
图11 不同旋转热流场的最大轴向与最大切向速度之比

4 结 论

在壁面有侧开缝的竖直通道内，以正庚烷液体为燃料所形成旋转火焰的实验与基于大涡数值技术的模拟研究得到：

1）基于大涡模拟技术的数值模拟方法可以较准确地模拟有侧开缝的竖直通道内液体燃料燃烧所形成的旋转火焰热流场.

2）通道壁面附近的切向速度绝对值均保持在100 cm／s左右，在60 cm高度时，由火焰中心向壁面方向的切向速度先迅速增大，到达最大值后又逐渐降低到100 cm／s附近，而在120 cm高度以上时，切向速度只有逐渐上升过程.

3）由火焰中心向通道两侧方向，科氏力与浮力之比值的变化规律近似呈现对称分布，均是先逐渐增大，而后又逐渐降低，最大比值发生在火焰外侧位置.相比于浮力，科氏力对流场的作用随着高度的增加而减弱，通道下半部分的科氏力对流场的影响较浮力大，而在通道的上部分，浮力则对流场起主要作用.

4）通道内旋转火焰热流场的最大轴向速度与最大切向速度之比的数值模拟结果与按文献［15］的计算方法得到实验计算结果符合较好，并且最大轴向速度约为最大切向速度的2倍.

［1］CHOW W K， HAN S S.Experimental investigation on onsetting internal fire whirls in a vertical shaft［J］.Journal of Fire Sciences， 2009， 27（6）： 529-543.

［2］FORTHOFER J， BUTLER B.Large scale fire whirls：can their formation be predicted？ ［C］／／Proceedings of 3rd Fire Behavior and Fuels Conference.Spokane，Washington，USA：IAWF，2010.

［3］EMORI R I， SAITO K.Model experiment of hazardous forest fire whirl［J］.Fire Technology， 1982， 18（4）：319-327.

［4］Soma S， Saito K.Reconstruction of Fire Whirls Using Scale Models［J］.Combustion and Flame， 1991， 86（3）： 269-284.

［5］ZHOU R，WU Z N.Fire whirls due to surrounding flame sources and the influence of the rotation speed on the flame height［J］.Journal of Fluid Mechanics， 2007，583：313-345.

［6］KUWANA K，SEKIMOTO K，SAITO K，et al.Scaling fire whirls［J］.Fire Safety Journal， 2008， 43（4）： 252-257.

［7］SNEGIREV A Y， MARSDEN J A， FRANCIS J， et al.Numerical studies and experimentalobservations of whirling flames［J］.International Journal of Heat and Mass Transfer， 2004， 47（12／13）： 2523-2539.

［8］MCGRATTAN K B，HOSTIKKA S，FLOYD J E，et al.Fire dynamics simulator （version5），technical reference guide［R］.Gaithersburg， Maryland： National Institute of Standards and Technology， 2007： 1018-5.

［9］霍岩.有限开口空间热驱动流大涡模拟和实验研究［D］.哈尔滨：哈尔滨工程大学，2010：8-15.

［10］HUGGETT C.Estimation of rate of heat release by means of oxygen consumption measurements ［J］.Fireand Materials， 1980， 4（2）： 61-65.

［11］PRASAD K， LI C， KAILASANATH K， et al.Numerical modelling of methanol liquid pool fires［J］.Combustion Theory and Modelling， 1999， 3（4）： 743-768.

［12］ZABRANSKY M， RUZICKA V.Heat Capacity of Liquidn-Heptane Converted to the International Temperature Scale of 1990［J］.Journal of Physical and Chemical Reference Data， 1994， 23（1）：55-61.

［13］WERNER H， WENGLE H.Large-eddy simulation of turbulent flow over and around a cube in a plate channel［C］／／In 8th Symposium on Turbulent Shear Flows.Munich， Germany： Springer Berlin Heidelberg， 1993：155-168.

［14］PEACOCK R D，RENEKE P A， DAVIS W D，et al.Quantifying fire modelevaluation using functional analysis［J］.Fire Safety Journal， 1999， 33（3）： 167-184.

［15］杨春英，武红梅，霍岩.小尺寸方形竖槽道火旋风的实验研究及火焰特征［J］.燃烧科学与技术，2011， 17（3）： 203-208.