自适应熵疫苗算子的免疫图像分割方法

王 辉，于立君，毕晓君，郭 晓

（1.哈尔滨工程大学 自动化学院，150001哈尔滨；2.哈尔滨工程大学信息与通信工程学院，150001哈尔滨）

图像分割作为图像处理中的一项重要环节，直接影响到后续检测、识别效果的好坏，图像分割方法的选择至关重要［1-4］.阈值分割法与其他方法相比，运算更为简单有效，因此被广泛应用到实时性要求较高的图像处理中.如何确定最佳阈值是利用该方法进行图像分割的关键环节.二维熵阈值法能很好的将图像信息用图像中像素点的灰度及其周围邻域的灰度均值表达出来，在图像分割中得到广泛应用.但是传统的二维熵阈值法采用一一试探法来搜索最优阈值，耗费大量的时间从而限制了该方法的应用.

疫苗算子通过接种疫苗来实现，它可以根据已知的入侵，从中提取表示入侵的特征信息生成，并对特征值进行编码构造疫苗.也可以在入侵检测的过程中动态地、自适应地提取疫苗［5-6］.疫苗算子能够使算法的记忆功能增强，本文将免疫优化机制［7］加入到图像分割中，并引入疫苗算子，并加入熵作为更新依据，不仅能够使解群中的多样性得到保持，而且加速了解群收敛到全局稳定点，使得算法的分割速度得以提高，得到比较理想的分割效果.

1 熵疫苗算子

疫苗主要用来记忆入侵过的抗原以及对应的适应度最高的抗体［8-9］.采用熵疫苗算子可以避免陷入局部最优，保证记忆抗体的多样性.

1.1 点灰度和区域灰度均值对

一幅图像一般表示成N×N个像素点，把每一个像素点均用二维形式表示（x，y），定义函数f（x，y） 为像素点（x，y） 的灰度函数，函数f（x，y）满足f（x，y） ≤L，其中L为图像的最大灰度值［10-13］．则在像素（x，y） 处的 3×3 邻域内，其灰度均值为

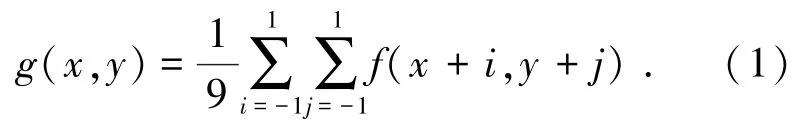
由此，原始图像中每一个像素点都可用其对应的点灰度和区域灰度均值对［f（x，y），g（x，y）］唯一表示，图像的这种二维表示形式共有L×L种可能的取值．若以二维矢量（S，T）分割图像，这里，1≤S，T≤L，则二维阈值化函数可以定义为式中 1 ≤b0，S，b1，T≤L．

下面研究点灰度和区域灰度均值对发生的概率．令图像中某像素点的灰度值为i，它周围邻域的灰度平均值为j的像素点个数为nij，则点灰度和区域灰度均值对（i，j）发生的概率pij为

式中分母N×N为图像中像素的总数，且

1.2 目标和背景的离散二维熵

二维灰度直方图是以i，j为自变量，pij为因变量构成的，如图1所示．

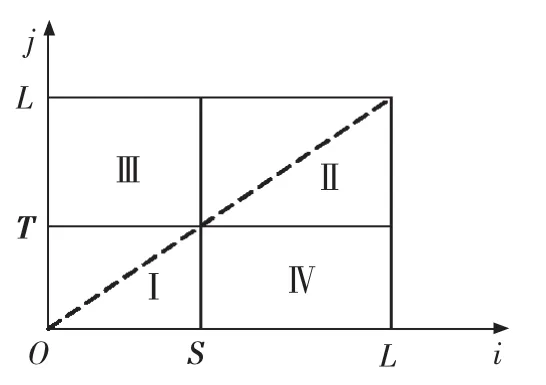
图1 二维灰度直方图

直方图上共有L×L个点，每个点的函数值即为pij．沿对角虚线分布的Ⅰ区和Ⅱ区表示图像中的目标和背景，Ⅲ区和Ⅳ区表示图像中的边界和噪声．

设二维灰度直方图Ⅰ区分布概率为PⅠ，Ⅱ区分布概率为PⅡ对各区域的概率pij进行归一化处理，设阈值为（s，t），则定义离散二维熵为

则Ⅰ区和Ⅱ区的离散二维熵分别为

式中：

Ⅲ区和Ⅳ区代表图像的边界和噪声，其出现的概率较小，可将其忽略，从而得到，则

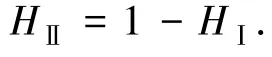
由式（5）可得

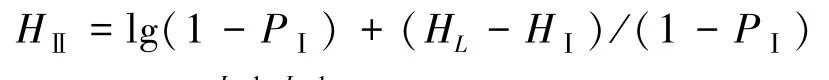
1.3 熵疫苗算子

根据信息熵原理，熵疫苗的提取采用图像熵作为判别函数熵的判别函数定义为

为使图像中有用的目标和背景的信息量最大，需要在Ⅰ区和Ⅱ区中利用二维最大熵法确定最佳阈值，并用点灰度和区域灰度值表示.则选取的最佳阈值向量满足

因此，当图像熵最大时，判断该抗体为当代最优抗体，加入疫苗库，成为熵疫苗.

2 自适应熵疫苗算子免疫图像分割

二维最大熵分割运算量大，耗费时间长，很难满足实时性要求［14-18］.本文采用一种自适应熵算子对阈值选取过程进行优化设计，加速最优阈值的生成过程，提高分割质量.

2.1 图像抗原及最优抗体

将待分割的图像作为入侵抗原集合X=｛X1，X2，…，Xn｝，X表示整幅图像，Xi（i=1，2，…，n） 表示待分割图像区域．将Xi视为入侵抗原，将分割阈值视为抗体，抗体对应于遗传操作中的染色体．当有抗原Xi入侵时，在产生的抗体中寻找最优抗体，即可得到最优分割阈值．得到最优分割阈值（s∗，t∗） 是本算法的最终目的．抗体编码时，量化成 16 位二进制基因a=｛a0，…a7，a8，…a15｝，其中，第1个阈值坐标s用前8个量化值表示，后8个量化值表示第2个阈值坐标t．由此可知此时搜索空间有2562个点．

2.2 熵疫苗库的建立及自适应更新

待分割图像的特征值主要用灰度直方图、最大和最小灰度等特征参数来表达［19-24］.根据特征参数判断是否需要分割抗原：0表示无需分割，1表示需要进行分割［25］.被分割的抗原记入熵疫苗库.

熵疫苗作为抗体疫苗进行提取，每代通过熵运算，提取当代最大熵疫苗，当疫苗库元素数量达到10时，若当代熵大于疫苗库中已存在的疫苗熵，则用该熵疫苗替换掉疫苗库中熵最小的疫苗，更新疫苗库，同时尽量避免相同的两个抗体出现在疫苗库中，以避免陷入局部最优，保证记忆抗体的多样性.使熵疫苗库的更新具有自适应性［26］.

2.3 初始抗体群生成

本文设定群体规模为N=20.当有抗原入侵时，首先判定抗原类别，然后根据特征参数与疫苗库中已知抗原进行匹配.如果是非已知抗原，则初始抗体群体全部随机产生，如果是已知抗原，则为保持群体多样性，群体中的15个个体由记忆抗体集合提供，其余5个仍然随机产生.

2.4 抗体群自适应更新

2.4.1 选择免疫优化算子

抗体群要完成自适应更新，首先要对抗体进行选择，本文给出免疫优化算子作为选择依据.免疫优化算子是受到免疫调节原理的启发，即免疫细胞和分子能够通过相互促进和抑制来调节免疫应答的强度及其正、负方向［27］.因此利用免疫优化算子可以完成抗体群抗体被选择的概率.被选择的抗体由抗体的个体浓度和适应度概率共同决定，即一个抗体被选择的概率为

其中

式中：Fi代表抗体i与抗原的适应度，表示整个抗体群个体适应度总和．

式中：Ki为抗体群中个体i的数量，N为抗体群所有个体总数量．

选择免疫优化算子由适应度算子和浓度算子相互制约，相互协调，不仅可以使适应度高的个体被保留，而且基于浓度的调节使得抗体群中多样性得到保证，避免“早熟”现象的发生.

2.4.2 交叉算子

交叉算子是要在上述所选择出来的部分抗体中进行交叉操作，目的是要在此基础上得到新的抗体，增加抗体多样性.

交叉算子定义为

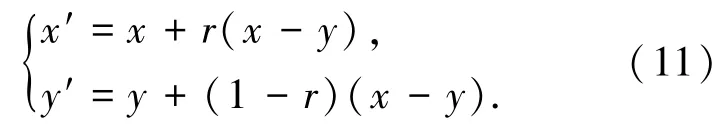
式中r的取值范围为［0，1］，选取的r值要使x′和y′的值符合图像灰度取值范围．

2.4.3 变异算子

通过前面交叉操作后，抗体的多样性虽然得到增加，但是毕竟交叉操作得到新抗体的范围有限，因此在交叉的基础上，选择出的另一部分抗体进行变异操作.本文在进行抗体变异时考虑个体适应度的影响，使个体的变异与其适应度成正比，即变异算子可定义为式中xmax表示父代中最优个体．

整个抗体自适应更新的算法流程图如图2所示.

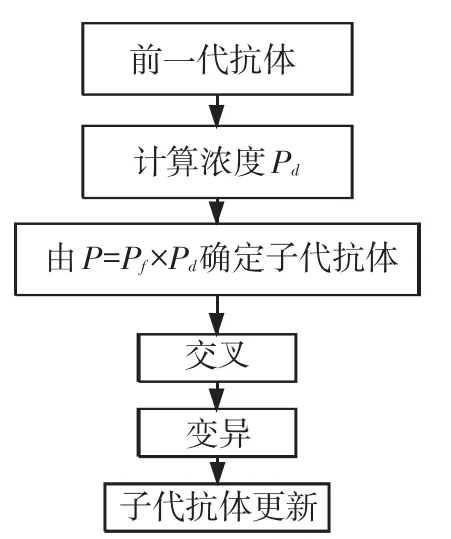
图2 更新算法流程图

3 实验结果及分析

仿真实验分别选取两幅木材疤痕占图像比例不同的木材图片作为原始图像，分别用传统穷尽法和本文提出的免疫优化算法实现图像中疤痕的分割.其中设定种群规模为20，选择概率为0.78，变异概率为0.012，最大迭代次数为50.若经过50代遗传算法的最优阈值都没有改变，则遗传算法结束，得到二维最优分割阈值结果.

图3是分割目标占图像比例较小的原始灰度图像，图4是分割后的图像.图5是分割目标占整幅图像比例较大的原始灰度图像，图6是对应的分割后的图像效果.对于分割后的图像，对分割后的疤痕图像进行数学形态学运算，包括腐蚀、膨胀以及开运算和闭运算消除残留的纹理噪声.图4和图6图像通过二值形态学运算后得到的结果如图7和图8所示.用白色表示分割出的目标，黑色为背景.表1列出的数据是分别用本文算法与传统穷尽法得到最佳阈值所用时间的比较.

图3 分割目标占整幅图像比例较小的原始图像

图4 图3的分割后效果

图5 分割目标占整幅图像比例较大的原始图像

图6 图5分割后的图像

图7 图4形态学运算后的图像

图8 图6形态学运算后的图像

表1 本文算法与传统算法进行阈值分割的时间比较

以上实验结果表明：利用本文所提出的算法对图像进行分割处理，能够得到较为理想的效果，而且在计算时间上也比传统的算法具有明显的缩短.此外，本文算法中选择的适应度函数是根据信息论中的最大熵原理定义的图像熵，将其作为熵疫苗算子加入到免疫算法中，提高了算法的整体性能.

4 结 论

本文用二维直方图表示图像并对图像分割问题运用二维最大熵准则进行处理，用免疫优化算法对其进行优化研究与实现.该方法将待处理的疤痕图像视为入侵抗原，最优分割阈值视为最优抗体，通过免疫优化，对抗体进行更新，最终将最优抗体输出，达到分割效果.最后通过实验进行了对比分析，证明了该算法的优势所在，即不仅能够准确分割疤痕图像而且还能明显提高分割效率.而且该算法不受分割阈值个数的限制，不需要因为阈值个数的改变而改变这个算法的流程.

［1］彭禹皓.图像分割技术综述［J］.计算机工程应用技术， 2013，（1）：140-141.

［2］王爽，夏玉，焦李成.基于均值漂移的自适应纹理图像分割方法［J］.软件学报，2010，21（6）：1451-1461.

［3］DASGUPTAA D， YUA S，NINO F.Recent advances in artificial immune systems： models and applications［J］.Applied Soft Computing， 2011， 11：1574-1587.

［4］万波，王泉，高有行.图像分割的误差分散半调算法［J］.西安电子科技大学学报，2009，36（3）：496-501.

［5］王辉，毕晓君，于立君，等.基于疫苗理论的变阈值免疫阴性选择算法［J］.哈尔滨工程大学学报，2011，32（1）：69-72.

［6］王辉，于立君，王科俊.一种可变模糊匹配阴性选择算法［J］.智能系统学报，2011，6（2）：178-184.

［7］莫宏伟，左兴权，毕晓君.人工免疫系统研究进展［J］.智能系统学报，2009，4（1）：21-28.

［8］王辉.可变模糊匹配阴性选择免疫算法研究［D］.哈尔滨：哈尔滨工程大学，2008.

［9］WANG Hui， GUO Xiao.An analysis of the minimal effective detector set based on the adjustable fuzzy matching negative selection algorithm of immune［C］／／IEEE ICISE.［S.l.］：［s.n.］， 2010： 965-968.

［10］LUMINITA A V， STANLEY J O.Modeling textures with total variation minimization and oscillating patterns in image processing［J］.Journal of Scientific Computing，2003，12 （1／2／3）：553-572.

［11］HUANG Wenlong， JIAO Licheng.Artificial immune kernel clustering network for unsupervised image segmentation［J］.Progress in Natural Science，2008，4：455-461.

［12］吴一全，张金矿.二维直方图θ-划分最大平均离差阈值分割算法［J］.自动化学报，2010，36（5）：635-643.

［13］JOBIN C M C， PARVATHI R M S.Segmentation of medical image usingK-means clustering and marker controlled watershed algorithm［J］.EuroJournals Publishing， 2012， 71（2）： 190-194.

［14］DERVIS K， BAHRIYE B.A powerful and efficient algorithm for numerical function optimization：artificial bee colony （ABC） algorithm［J］.Journal of Global Optimization， 2007 （3）：459-471.

［15］ZOU En， LIXiangfei， ZHANG Taishan.Fuzzy controller based on chaosoptimaldesign and its application［J］.Journal of Central South University Technology， 2004， 11（1）：98-101.

［16］郭臻，陈远知.图像阈值分割算法研究［J］.中国传媒大学：自然科学版，2008，15（2）： 77-82.

［17］李艳灵，沈轶.基于空间邻域信息的FCM图像分割算法［J］.华中科技大学学报，2009，37（6）：56-59.

［18］WANG Xiangyang， BU Juan.A fast and robust image segmentation using FCM with spatial information［J］.Digital Signal Processing， 2010，20（4）： 1173-1182.

［19］SIANG T K， MAT I N.Color image segmentation using histogram thresholding—Fuzzy C-means hybrid approach［J］.Pattern Recognition， 2011， 44（1）：1-15.

［20］NING Jifeng， ZHANG Lei， ZHANG David.Interactive image segmentation by maximal similarity based region merging［ J］.Pattern Recognition，2010，43（2）：443-456.

［21］HOU Xuefeng， SHANG Yuanyuan.Research and simulation on the image segmentation algorithm with corn image based on HSI Color model［J］.Advanced Materials Research， 2012， 459： 128-131.

［22］KIM J G， NOBLE J A， BRADY J M.Probabilistic models for shapes as continuous curves［J］.J Math Imaging Vision， 2009， 33（1）：39-65.

［23］朱蕾.木材表面缺陷图像识别的算法研究［D］.南京：南京林业大学，2011.

［24］ARBELAEZ P， MAIRE M， FOWLKES C， et al.Contour detection and hierarchical image segmentation［J］.IEEE Transactionsonn Pattern Analysisand Machine Intelligence， 2011， 33（5）： 898-916.

［25］CUERVAS E， OSUNA-E V， ZALDIVAR D.Multi threshold segmentation based on artificialimmune systems ［J］.Mathematical Problems in Engineering，2012， 2012： 874761.

［26］ARDESHIR G.Design and recovery of 2-D and 3-D shapes using rational Gaussian curves and surfaces［J］.International Journal of Computer Vision， 2006（5）：83-85.

［27］DASGUPTA D， YU S， NINO F.Recent advances in artificial immune systems： models and applications ［J］.Applied Soft Computing， 2011，11（2）：1574-1587.