正弦激励法在传感器校准中的新应用*

杨雪松， 李长春， 母东杰， 陈 策

(北京交通大学 机械电子控制工程学院，北京 100044)

0 引 言

国家标准GB 7665—87对传感器的定义是：“能感受规定的被测量件并按照一定的规律(数学函数法则)转换成可用信号的器件或装置，通常由敏感元件和转换元件组成”。因而传感器校准的本质是通过分析被测量的实际值与传感器输出来确定这种规律(数学函数法则)。当然受测量手段精度的限制和随机噪声的影响，被测量的实际值是很难获取的，人们往往是以足够精度的测量值替代之。于是选择怎样一种方法来获取该测量值成为了传感器校准的关键问题之一。

以速度的测量为例，常见的方法有空间滤波器法、相关法、利用多普勒效应或电磁感应原理、加速度积分法和位置微分法。文献[1]采用瞬时平均速度获得近似的标准速度，本质上属于空间滤波器方法，获得的速度实际上是极短时间段内平均速度而非瞬时速度。再以加速度传感器的校准为例，目前主流的校准方法有振荡校准法和冲击校准法。其中,振荡校准法即正弦激励方法，是一种较为简单且精度又高的校准方法[2]，因此,该方法作为一种标准方法被包含在ISO 16063—11(基于激光干涉仪的绝对振动校准法)中，并得到广泛的运用[3]。相比于振荡校准法，冲击法更适用于高gn值的加速度传感器校准，且在高频段的相位不确定度更小[4]。这2种方法的优点是可以对传感器进行高精度的动态标定，缺点是必须使用激光干涉仪，成本高不易推广。

本文采用的速度传感器校准方法是正弦激励法，实验平台采用电液位置伺服系统，该平台具有结构简单、成本低、易于推广的特点。信号处理方法采用基于最小二乘的正弦逼近方法，该方法不仅能够得到真正意义上的瞬时速度信号，而且能够在存在噪声的情况下取得最优解。

上述方法还可以被应用到测量定回转轴角加速度的问题中。长期以来，由于角加速度传感器的成本远高于线加速度传感器，因此,工程人员期望找到一种用线加速度传感器测量角加速度的方法。经过多年的发展，国内外学者分别提出了六加速度计、九加速度计和十加速度计的组合方法[5]来获取刚体在所有自由度方向上的运动状态。不过在一般的机电系统中定轴回转的状态是最为常见的，文献[6]提出了一种用2只双轴线加速度计获取定轴回转状态的方法。相比之下，在适当的假设条件下，这种改进的正弦逼近算法可以实现用一只单轴加速度计来完成角加速度的测量，显然该方法是更经济实用的。

1 校准算法

校准算法的核心是基于最小二乘法的正弦信号逼近方法，文献[7]提出了一种辨识正弦信号幅值和相位差的方法。但是，实际的传感器信号常包含有偏置，使得上述方法不再适用，因此，本算法在原算法的基础上加入了偏置项的辨识，大大提高了计算精度。

假设有一正弦信号v(t)被以采样频率fs采样，得到一组M个采样点。待辨识的信号如下

v(t)=Vsin(ωt+φ)+W.

(1)

展开上式可得

v(t)=C0sinωt+C1cosωt+C2.

(2)

其中，C0=Vcosφ,C1=Vsinφ,C2=W。

需要确定的参数为C0，C1，C2，为此需要应用最小二乘法得到该参数的最小二乘估计。假设采样频率为fs，得到M个采样点，通过采集系统可得采样点的值v(t0)，v(t1)，…，v(tM-1)，可得到v(t)的测量残差为

vi=C0sinωti+C1cosωti+C2-v(ti),

i=0,1,…,M-1.

(3)

其残差平方和为

(4)

令Φ0(t)=sinωt，Φ1(t)=cosωt，则有

(5)

根据最小二乘原理，由极小值存在的必要条件，求残差平方和[v2]的极小值，可由式(5)求出对Cj(j=0,1,2)参数的偏导数，并令其为0，如式(6)所示

(6)

由上式可获一个方程组，这一方程组的解即为参数Cj的最小二乘估计。为此，根据式(6)可导出方程组

(7)

式中Φ0=Φ0(ti),Φ1=Φ1(ti)。为便于计算可以将方程组(7)写成矩阵的形式

ATAC=ATb.

(8)

其中

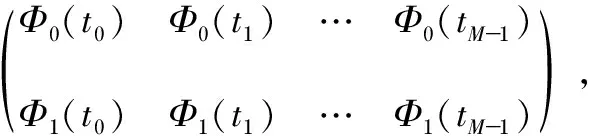
CT=[C0C1C2]，

bT=[v(t0)v(t1) …v(tM-1)].

若式(8)中的ATA为非奇异矩阵，则C必有唯一解，其矩阵表达式为

C=(ATA)-1ATb.

(9)

综上所述，通过最小二乘法可以辨识出参数Cj，进一步可以推导出正弦信号的幅值、相位以及偏置。

2 实验研究

为证明上述算法的有效性，分别设计了使用位移传感器标定速度传感器的试验和利用线加速度测量定回转轴角加速度的实验。

2.1 实验一

实验系统由：阀控液压缸、传感器、数据处理系统组成，如图1所示。实验开始后，阀控液压缸在控制系统的闭环控制下进行正弦运动，数据采集系统采集位置传感器信号和速度传感器信号，再利用正弦信号参数辨识算法分别得到位置信号和速度信号的幅值Ap,As,则速度传感器的灵敏度S(V/(m·s-1))可由式(10)得到

(10)

其中,Ap的单位是m，As的单位是V，因为正弦位置信号的导数是频率相同但幅值增大了ω倍的余弦信号，因此，在这里ω是一个无量纲比例系数，数值上等于信号的角频率。

图2展示了一组实验过程中位置与速度传感器的信号，如图所示位置信号的信噪比大，速度信号的信噪比小，因此，先利用正弦信号参数辨识算法去除噪声的影响，而后利用较理想的位置信号的微分值校准速度传感器的灵敏度是合理的。校准结果如表1所示，为方便计算表中的幅值Ap，As使用dB为单位，不影响计算结果。对实验数据求平均得到该速度传感器的灵敏度S为0.136 8(V/(m·s-1))，其标准差为0.000 55，因此，该校准方法具有较高的精度。

图1 实验一系统组成示意图

图2 频率1 Hz的正弦激励下的传感器信号

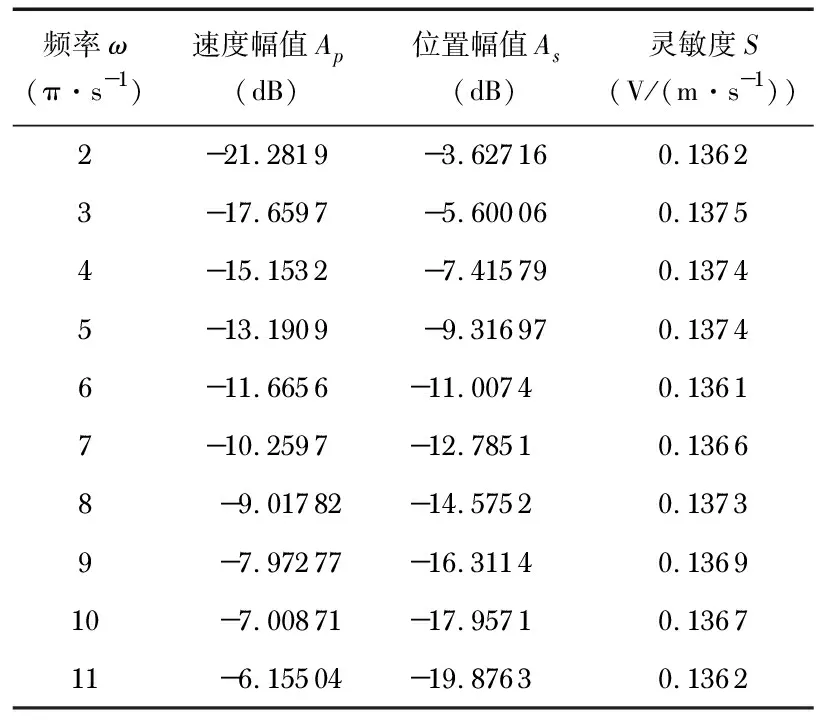
表1 各频率点速度传感器灵敏度校准结果

2.2 实验二

当线加速度计被安放在定回转轴的切线方向上时，线加速度计就可以测量出角加速度。不过当该回转轴平行于大地(或者说除非其垂直于地面)时，重力加速度就会在切线方向产生一个分量，如图3所示，该分量是转角θ的正弦函数gsin(θ+π/2)，在角加速度的测量中应当将其去除。试验系统由伺服电机、单轴线加速度计、测控系统组成。首先测控系统发出指令使伺服电机匀速转动，实时采集伺服电机反馈的转角信号和加速度计的反馈信号,令θ=ωt，其余算法与第二部分介绍的校准算法一致，即可得到由重力产生的加速度信号与转角的函数关系，如式(11)所示。从而可以根据此函数关系对重力加速度的切线方向分量进行补偿。图4显示了当电机回转轴进行匀速转动时，加速度信号补偿前后的情况，补偿效果非常理想。

图3 重力加速度切线分量与转角关系图

g′(θ)=Agsin(θ+φg)+Wg,

(11)

式中g′为线加速度传感器绕回转轴匀速转动时输出的信号，Ag,φg,Wg分别为该函数的幅值、初始角和偏置。

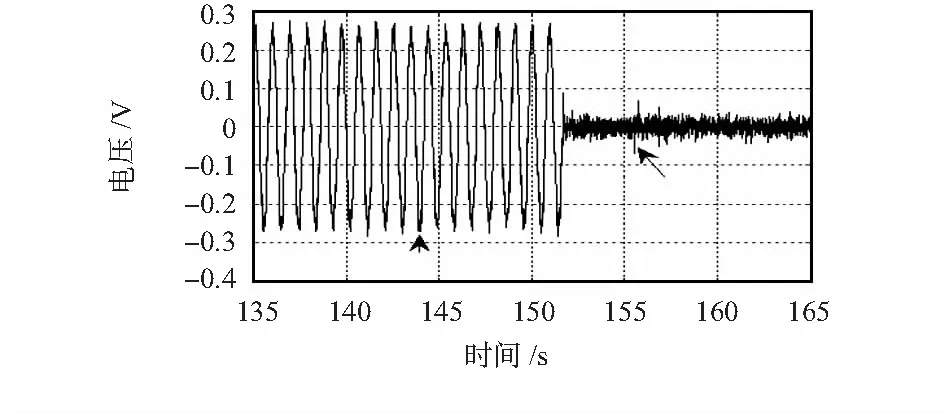
图4 回转轴匀速转动时加速度信号对比图

3 结 论

1)实际的传感器信号常存在零位漂移，因此,新的正弦逼近算法在老算法的基础上增加了对信号偏置量的辨识。该方法可适用于各类型的速度、加速度传感器的静态灵敏度校准，实验结果表明,该方法具有很高的精度。

2)该方法可用于补偿重力加速度对于绕定回转轴转动的线加速度的影响，从而可以使单轴线加速度具备测量角加速度的能力，实验结果表明:该方法获得了极佳的补偿效果。

参考文献:

[1] 李亚荣，付继华.绝对式线速度传感器标定系统原理与实现[J].大连铁道学院学报,2003，24(1):93-95.

[2] 大畑正已，吴 凡.压电式加速度传感器的校准方法[J].国外计量，1988(5)：23-24.

[3] Veldman C S.A novel implementation of an ISO standard method for primary vibration calibration by laser interferometry[J].Metrologia，2003,40:1-8.

[4] Link A，Taubner A， Wabinski W，et al.Calibration of accelero-meters:Determination of amplitude and phase response upon shock excitation[J].Measurement Science & Technology，2006,17:1888-1894.

[5] 费 维，刘正士，郑传荣.几种角加速度传感器的工作原理及其应用[J].机床与液压，2005(1):145-146.

[6] 陶建峰，刘成良，王旭永.用线性加速度计测量定轴回转系统状态的理论研究[J].上海交通大学学报，2006，40(4):553-557.

[7] 程 捷.检测正弦信号相位差算法的研究[J].计量技术，1997(10):28-30.