PCA-LSSVM方法的控制系统性能评估

蔡宏斌 苏成利

(辽宁石油化工大学信息与控制工程学院，辽宁 抚顺 113001)

PCA-LSSVM方法的控制系统性能评估

蔡宏斌 苏成利

(辽宁石油化工大学信息与控制工程学院，辽宁 抚顺 113001)

为了准确地评价多变量控制系统的性能，并简化其评价过程的计算复杂度，提出了基于主元分析(PCA)与最小二乘支持向量机(LSSVM)相结合的多变量控制系统性能评价方法。该方法将原始自变量数据通过PCA方法进行降维处理，利用二次损失函数取代支持向量机中的不敏感损失函数，将不等式约束变为等式约束，从而将二次规划问题转变为线性方程组的求解，并对LSSVM的参数选取做了改进。该方法在性能评价过程中不需要求解系统关联矩阵，简化了求解的复杂性。仿真实例验证了PCA-LSSVM性能评价方法更能反映控制系统真实性能。

最小二乘支持向量机 多变量控制系统 主元分析 关联矩阵 性能指标 性能评价

0 引言

评估控制系统的性能对于企业的发展具有重大意义。目前，相继出现了不少新的研究成果［1］。工业控制回路大多是多变量的，因此研究多变量控制系统的性能评估方法具有更长远的意义［2］。

在使用最小方差控制(minimum variance control，MVC)基准方法进行控制系统性能评价时，需要完整的过程模型和关联矩阵的信息［3－4］。有学者采用一个实用的次优多变量MVC控制基准，即只需要关联矩阵的阶次而不必构造出关联矩阵［5］。利用Markov参数和闭环运行数据的性能评估方法也只需要获知过程的时滞阶次信息［6］。

本文研究了主元分析(principal component analysis，PCA)与最小二乘支持向量机相结合的性能评价算法。该方法先将原始数据通过主元分析方法进行降维处理;再把获得的新主成分使用最小二乘支持向量机进行训练;然后再通过建立新模型计算出控制系统性能指标，得到更为准确的性能评价指标。

1 主元分析

主元分析的对象是样本点×定/变量类型的数据表，其目标是对这种多变量的平面数据作最佳综合简化。也就是说，要在力保数据信息丢失最少的原则下，对高维变量空间进行降维处理。

设Xn×m为数据矩阵、n为样本数、m为变量个数，矩阵的每一列对应于一个变量，每一行对应于一个样本。矩阵X可以分解为m个向量的乘积之和，即:

式中:ti为得分向量，也称主元;pi为负荷向量。式(1)也可以写成以下矩阵形式:

式中:T为得分矩阵，T= t1t2… tm[

];P为负荷矩阵，P= [p1p2… pm]。

当矩阵X的变量间存在一定程度的线性相关时，X的变化将主要体现在最前面的几个负荷向量方向上，X在最后面的几个负荷向量上的投影将会很小，它们主要是由测量噪声引起的。这样就可以将X进行主元分解后写成式(3)的形式:

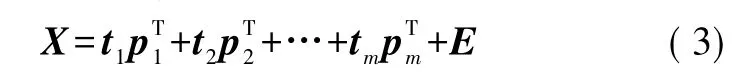
式中:E为误差矩阵。忽略E，往往会起到清除测量噪声的效果。

对X进行主元分析实际上等效于对X的协方差矩阵XTX进行特征向量分析。将协方差矩阵的特征值做如下排列:λ1≥λ2≥…≥λm，那么与这些特征值对应的特征向量P1，P2，…，Pm即为矩阵的负荷向量。特征值的大小反映了对应的主成分样本的离差程度，所选主元个数可通过累积方差百分比(comulative percent variance，CPV)来确定。采用这种方法，需要人为选定一个期望的CPV(如85%)作为准则，当CPV大于期望值时，对应的k值就是应保留的主元个数。在实际应用中，可根据实际情况，以能反映对象的绝大部分动态信息来决定主元的个数［7－8］。

2 最小二乘支持向量机

支持向量机的基本思想为:给定l个样本数据( x1，y1)，( x2，y2)，…，( xl，yl)∈Rn×R，其中 x为样本输入，y为样本输出。首先，利用非线性映射φ(· )，将输入向量从原空间Rn映射到一个高维特征空间(Hibert空间);然后，在这个高维特征空间中，采用结构风险最小化的原则构造最优决策函数，并利用原空间的核函数取代高维特征空间的点积运算以避免复杂运算，从而将非线性函数估计问题转化为高维特征空间中的线性函数问题。设构造的最优决策函数具有如下形式:

求解式(4)的目的就是利用结构风险最小化原则，寻找参数ωT和b。寻找ωT和b等价于求解下面的优化问题:

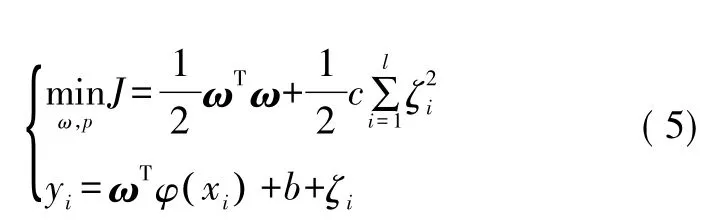
通过式(5)的对偶形式，可以求出它的最优解。式(5)的对偶形式可以根据目标函数和约束条件建立Lagarangian函数，并对建立的Lagarangian函数进行求偏导。根据其偏导方程，可将求解的优化问题转化为求解线性方程，定义核函数代替非线性映射，最后得到最小二乘支持向量机的估计函数(即系统模型)为［8］:

式中:K( x ，xi)为满足Mercer条件的任意对称函数。

3 性能评估算法

对于多变量控制系统，先取一组长度为n、输入变量个数为m的数据，再取一组长度为n的输出数据。在对主成分进行计算时，首先必须对输入矩阵X的数据进行归一化处理，以消除指标量纲的影响。由标准化公式所计算得到的输入数据x′ij的标准化值为:

本文采用由式(7)所得标准化值来计算标准化处理后的数据变量间的相关矩阵，从整体上研究因变量Y和自变量数组X之间的相关性。其相关矩阵R表示如下:

定义前k个主成分的累积贡献率为:

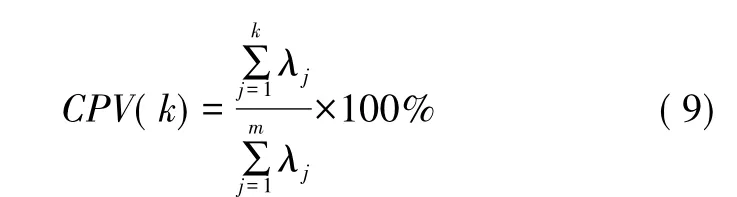
式中:k＜m。当CPV(k)≥85%时，说明前k项主元已达到输入数据信息总量的要求，那么前k项主元也就可以代表原来m项输入变量。

本文利用主元分析方法进行数据压缩和信息抽取，消除变量之间的相关性;再利用最小二乘支持向量机对提取的PCA主成分进行训练，获得其系统模型。

在进行支持向量机训练之前，首先需要选定核函数的形式，本文选用高斯核函数。在选定核函数后，还要选择合适的核参数σ和误差惩罚参数c。关于这两个参数的选择，由于不同样本集的最优参数值是变化的，这可能影响评估结果，因此本文计算时对参数进行动态选取。

动态选取时，首先规定误差惩罚参数集和核参数集，从参数集中选取参数分别进行组合;然后对最小二乘支持向量机进行训练;最后采用测试集检验，选出最佳的参数组合作为模型的最终参数。

最小二乘支持向量机考虑采用下式对未知模型进行辨识。

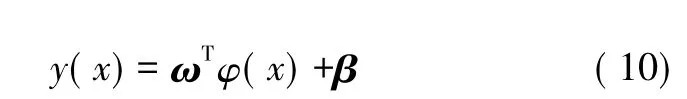
式中:φ ( ·)为非线性函数，它把数据集从输入空间Rn映射到特征空间R，使输入空间中的非线性拟合问题变为高维特征空间中的线性拟合问题;ω和β为待求参数。

根据结构风险最小化原则，上述拟合问题可表示为如下约束优化问题:

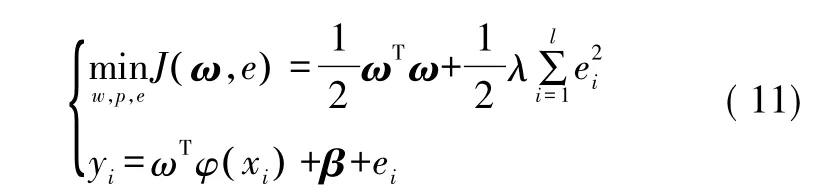
式中:ωTω为控制模型的复杂度;λ为正规化参数;ei为误差项。

为求解式(11)，可把约束优化问题转变为无约束优化问题，建立拉格朗日函数，得:

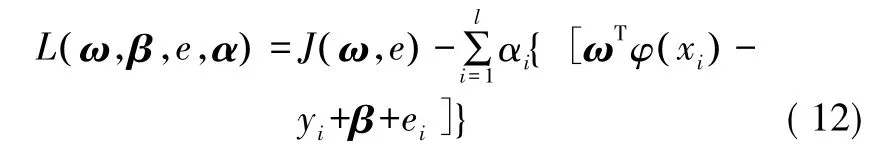
式中:αi为拉格朗日乘子。

求解上述优化问题又可转换为解线性方程:

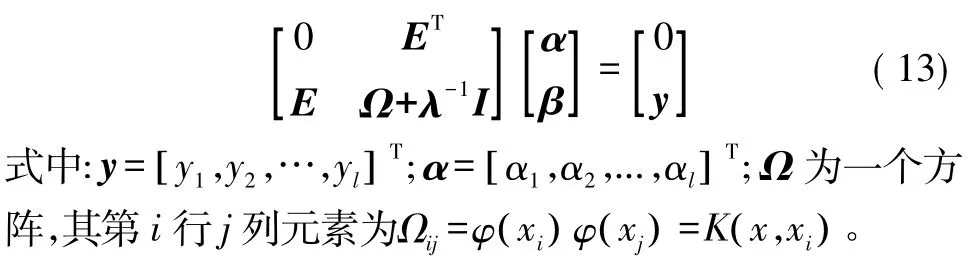
采用最小二乘法求出α与β，可得未知模型的拟合函数，即训练数据集的逼近为:

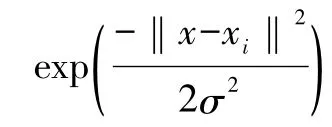
根据式(14)求得的输入输出间的系统模型，可求得残差的方差为:

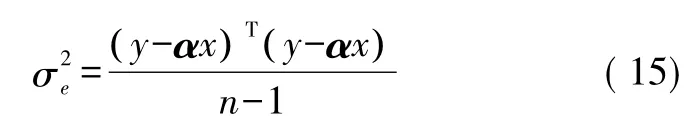
由式(15)可以求出方差σ2e的估计值。方差σ2e和实际输出数据方差σ2y的比值，就是所求控制器的性能指标η(d)，其表达式为:

通过对η(d)值的大小变化进行分析，便可对当前控制器的实际运行性能进行评价。

基于PCA-LSSVM的辨识模型步骤如下。

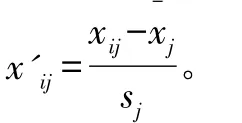
③找出所有累积方差百分比大于给定值(85%)的主元个数k，从而求出主元。这样通过主元分析可将n维输入变量转变为k维主元变量。

④寻找误差惩罚参数集和核参数集。

⑤从误差惩罚参数集和核参数集这两个参数集中选取参数分别进行组合，并利用所选的参数，进行最小二乘支持向量机训练。

⑥利用最小二乘支持向量机辨识模型，并用辨识好的模型进行性能评估。

4 仿真验证

控制系统的各函数定义如下，其过程控制模型为:

式中:k为过程模型变化量。干扰模型为:

干扰为二维零均值、协方差矩阵为Σa=1.36I的白噪声序列。

系统采用PI控制器，可得:式中:q－1为后移算子。

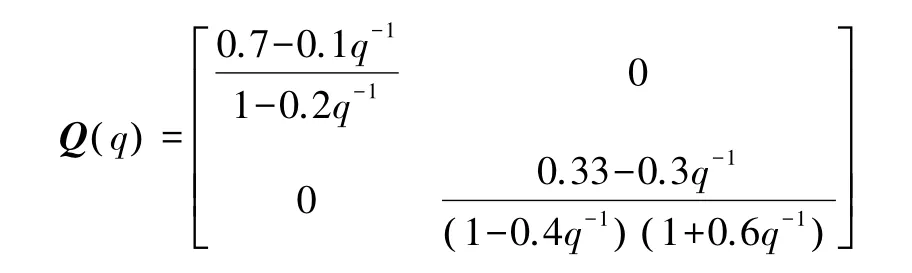
为了验证PCA-LSSVM性能评价方法的有效性，将本文方法与基于最小方差的性能评估方法进行对比研究。系统白噪声干扰信号如图1所示。

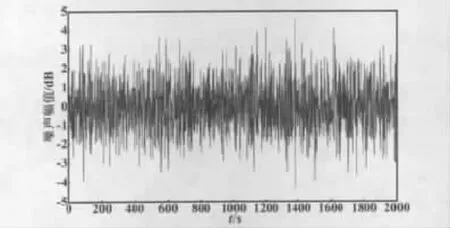
图1 系统白噪声干扰信号Fig.1 White noise interference signal of the system

①过程模型参数k固定时的评价验证

当k=1时，从仿真系统中采集2 000个仿真数据，然后将该数据按时间分成10组，每组包含200个数据点，分别采用最小方差(MVC)和本文提出的PCALSSVM性能评价方法评价控制器的性能。

控制器的基准性能指标如图2所示。

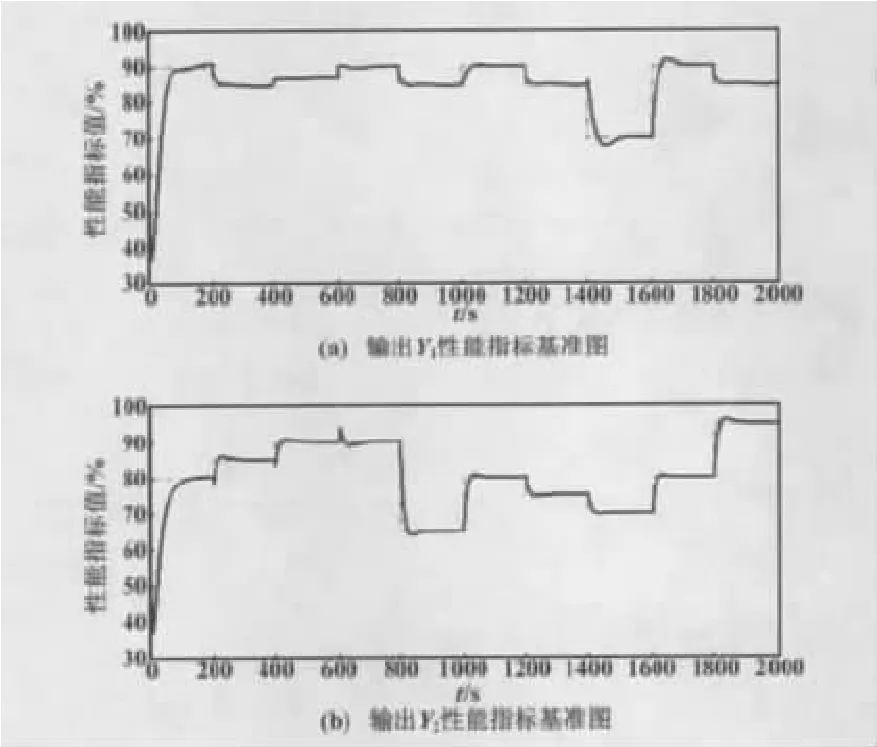
图2 输出Y性能指标基准图(k=1)Fig.2 Reference figure of the output Y performance indexes(when k=1)

性能评价效果如图3所示。由图3可以看出，在这个系统中，采用本文评价方法得出的评价结果比最小方差(MVC)评价结果误差小，贴近基准值;而最小方差评价结果忽大忽小，波动较大，致使评价结果不准确，并且突然对系统施加扰动时，相对而言本文提出的性能评价方法要比最小方差(MVC)性能评价方法更敏感些。由此可以得出，当对同一系统不同时间段的控制器进行性能评估时，使用PCA-LSSVM性能评价方法得到的评价结果要优于最小方差(MVC)性能评价方法，性能指标变化幅度比较小，更贴近实际情况。

图3 输出Y性能评价结果图(k=1)Fig.3 Evaluation results of the output Y performance(when k=1)

②过程模型参数k变化时的评价验证

当参数k从1变化到10时，在这10个不同参数情况下，从仿真系统中各采集200个数据点，同样采用最小方差(MVC)和PCA-LSSVM两种性能评价方法，评价控制器在不同过程模型下的性能。控制器的基准性能指标如图4所示。

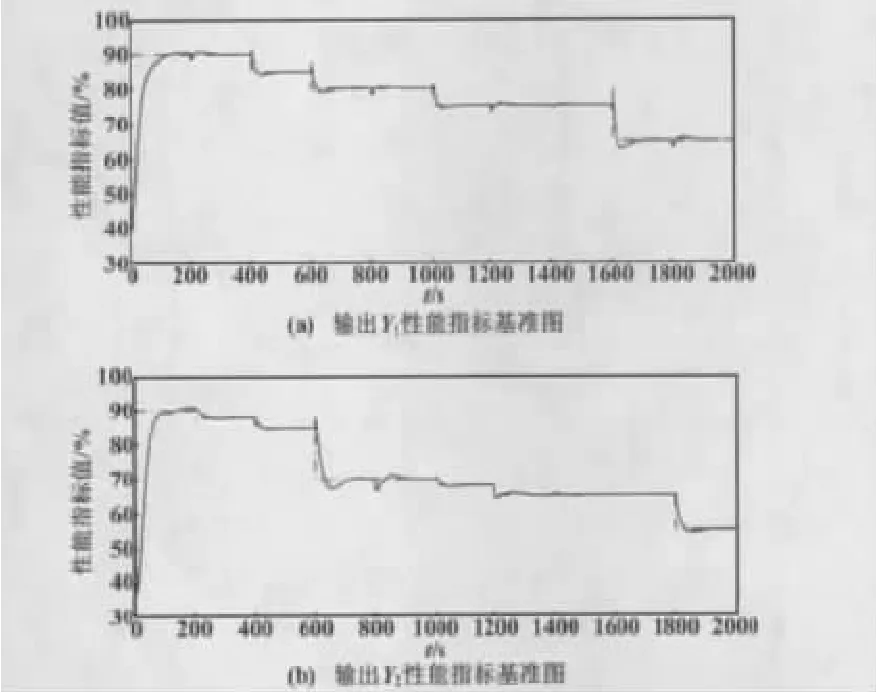
图4 输出Y性能指标基准图(k变化时)Fig.4 Reference figure of the output Y performance indexes(when k changes)

性能评价结果如图5所示。从图5可以看出，当增大系统过程模型参数k时，整个系统性能呈现下降趋势，当k取10时，性能指标急剧下降到50%左右。此外，当系统过程模型对象参数变化时，同时采用最小方差(MVC)性能评价方法和PCA-LSSVM性能评价方法对系统进行评价。最小方差(MVC)评价方法错估了系统真实性能，对模型参数变化不是很敏感;而本文方法的评价结果比较接近真实基准值，误差很小，可以反映出系统的真实性能。同时本文性能评价方法不需要求解系统关联矩阵，大大简化了计算的复杂度。因此，采用PCA-LSSVM性能评价方法对多变量系统进行性能评估具有一定的真实性和可靠性。

图5 输出Y性能评价结果(k变化时)Fig.5 Evaluation results of the output Y performance(when k changes)

5 结束语

本文研究了基于PCA-LSSVM方法的多变量控制系统性能评价方法，通过仿真验证了PCA-LSSVM方法对于多变量控制系统的性能评估。该方法计算得出的性能指标误差小，接近真实基准值，对系统变化敏感，指标变化曲线比较平稳。该性能评价指标不但可以反映系统的真实性能，而且不需要求解相关方程，就可以计算得出评价结果。

［1］ Sun Z，Qin S，Singhal A，et al.Performance monitoring of modelpredictive controllers via model residual assessment［J］.Journal of Process Control，2013(23):473－482.

［2］ Harris T，Yu W.Variance decompositions of nonlinear dynamic stochastic systems［J］.Journal of Process Control，2010，20(2):195－205.

［3］ Yuan Q L，Lennox B.Control performance assessment for multivariable systems based on a modified relative variance technique［J］.Journal of Process Control，2009(19):489－497.

［4］ Fu R，Xie L，Song Z，et al.PID control performance assessment using iterative convex programming［J］.Journal of Process Control，2012(22):1793－1799.

［5］ Tian X M，Chen G Q，Chen S.A data-based approach for multivariate model predictive control performance monitoring［J］.Neuro computing，2011(74):588－597.

［6］ Jelali M.An overview of control performance assessment technology and industrial applications［J］.Control Engineering Practice，2006，14(5):441－466.

［7］ Jeng J.Adaptive process monitoring using efficient recursive PCA and moving window PCA algorithms［J］.Journal of the Taiwan Institute of Chemical Engineers，2010，41(4):475－481.

［8］ Hu M Q，Chen Y Q，Kwok J.Building sparse multiple-kernel SVM classifiers［J］.IEEE Transactions on Neural Networks，2009，20(5):827－839.

Performance Assessment Based on PCA-LSSVM for Control System

In order to evaluate accurately the performance of multi-variable control system and simplify the computational complexity of the evaluation process，the performance assessment method based on the combination of principal component analysis(PCA)and least square support vector machine(LSSVM)for multi-variable control system is proposed.The dimension reduction of the original independent variables is conducted by PCA method;the insensitive loss function in SVM is replaced by quadratic loss function，and the inequality constraints is replaced by equality constraints，thus the quadratic programming is converted into the solution of linear equations;in addition，the selection of parameters of LSSVM is improved.The solving of system associated matrix is not necessary with this method for performance assessment，and the solving complexity is simplified.The practical example of simulation verifies that the PCA-LSSVM method better reflects the real performance of the control system.

Least square support vector machine Multi-variable control system Principal component analysis Associated matrix Performance indexes Performance evaluation

TP13

A

辽宁省科技攻关基金资助项目(编号:2011216011)。

修改稿收到日期:2013－04－10。

蔡宏斌(1987－)，男，现为辽宁石油化工大学控制理论与控制工程专业在读硕士研究生;主要从事工业过程的先进控制与优化、控制器性能评估方面的研究。

行业信息