容积粒子滤波在紧耦合SINS/GPS导航系统中的应用

任 波 李 强，2 赵 晴 李 浩

(沈阳理工大学装备工程学院1，辽宁 沈阳 110159;

中国人民解放军66347部队2，河北 保定 071000;中国人民解放军61267部队3，北京 101114)

容积粒子滤波在紧耦合SINS/GPS导航系统中的应用

任 波1李 强1，2赵 晴1李 浩3

(沈阳理工大学装备工程学院1，辽宁 沈阳 110159;

中国人民解放军66347部队2，河北 保定 071000;中国人民解放军61267部队3，北京 101114)

紧耦合SINS/GPS导航系统的数据融合过程存在高维状态和非线性混合模型，采用常规的线性卡尔曼滤波很难处理;而一般的非线性粒子滤波存在粒子退化和样本枯竭的问题。对此，提出将容积粒子滤波(CPF)算法应用于SINS/GPS组合导航系统。CPF利用容积卡尔曼滤波算法得到粒子滤波(PF)的重要性密度函数，并将最新量测值融入系统状态的转移过程中，由此产生的预测样本接近于系统状态的真实后验概率的样本。仿真结果表明，CPF算法的估计性能明显优于标准PF。

容积粒子滤波(CPF) SINS/GPS组合导航 非线性系统 卡尔曼滤波 数据融合

0 引言

捷联惯性导航系统(strap-down inertial navigation system，SINS)具有自主性和抗干扰能力强的优点，而全球定位系统(GPS)能提供全球高精度的三维实时导航信息，将SINS和GPS二者相组合，可以实现优势互补，提供高精度、全天候的导航服务［1］。SINS/GPS组合导航系统在航空航天、精确制导武器、大地测量和智能交通系统等领域具有很好的使用价值，越来越受到人们的关注。

紧耦合方式是将GPS系统和SINS系统作为整体进行设计，将伪距和伪距率作为观测量，利用现代滤波方法实现SINS与GPS的组合。在这种情况下，系统方程是非线性的，卡尔曼滤波难以直接处理。粒子滤波(particle filter，PF)直接采用非线性模型，具有较好的估计精度，受到学者的青睐［2］。但在 SINS/GPS组合导航系统的数据处理过程中，需要考虑陀螺加速度计的随机误差、漂移以及GPS的各种噪声，且系统方程的状态维数多达20维。随着维数的增加，粒子滤波本身的计算量也急剧增加，很多常规的粒子滤波算法不能满足实时性的要求［3］。因此，本文采用一种最新提出 的 非 线 性 滤 波——容 积 粒 子 滤 波［4－5］技 术(cubature particle filter，CPF)来解决紧耦合 SINS/GPS组合导航系统的数据融合问题。

1 容积粒子滤波

选择重要性概率密度是克服标准粒子滤波方法中粒子退化的关键。较之于扩展卡尔曼滤波器算法(extended Kalman filter，EKF)和无损卡尔曼滤波(unscented Kalman filter，UKF)，容 积 卡 尔 曼 滤 波(cubature Kalman filter，CKF)更容易产生真实反映函数分布的重要性概率密度，CKF能够使建议性密度函数更加接近于真实后验概率密度。动态非线性系统采用以下两个离散的系统方程表示。

①状态方程:

②量测方程:

以上两式中:xk和zk分别为k时刻系统的状态向量和观测向量;vk和wk分别为相互独立的系统噪声和观测噪声，wk～N(0，Qk)，vk～N(0，Rk)。

1.1 容积卡尔曼滤波

CKF算法［6］将非线性滤波归结为非线性函数与高斯概率密度乘积的积分求解问题。基于高斯假设的贝叶斯算法采用2n个等权值的求容积点实现非线性逼近。在解决高维非线性滤波问题方面，CKF具有较高的数值稳定性和滤波精度。根据求容积规则，可得:

CKF框架结构服从贝叶斯滤波结构，其算法流程可参考文献［6］。

CKF算法流程概括如下。

①初始化

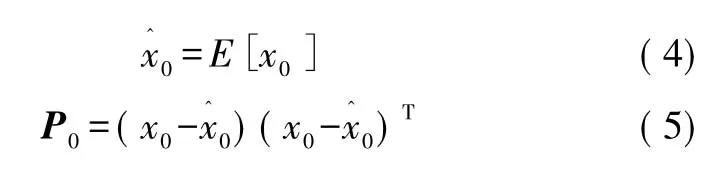
②时间更新

假设(k－1) 时刻后验概率分布 p(xk－1|Zk－1)=N(xk－1;x^

k－1|k－1，Pk－1|k－1)已知，采用 Cholesky 或奇异值方法分解协方差。③测量更新

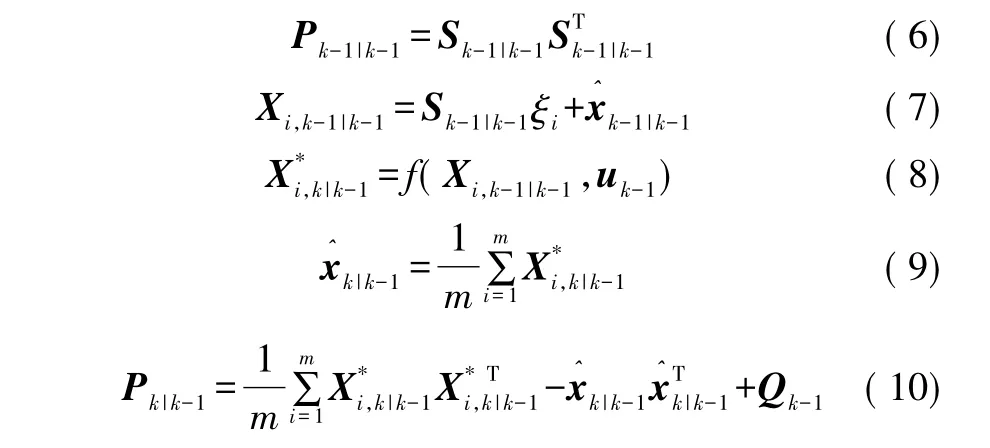
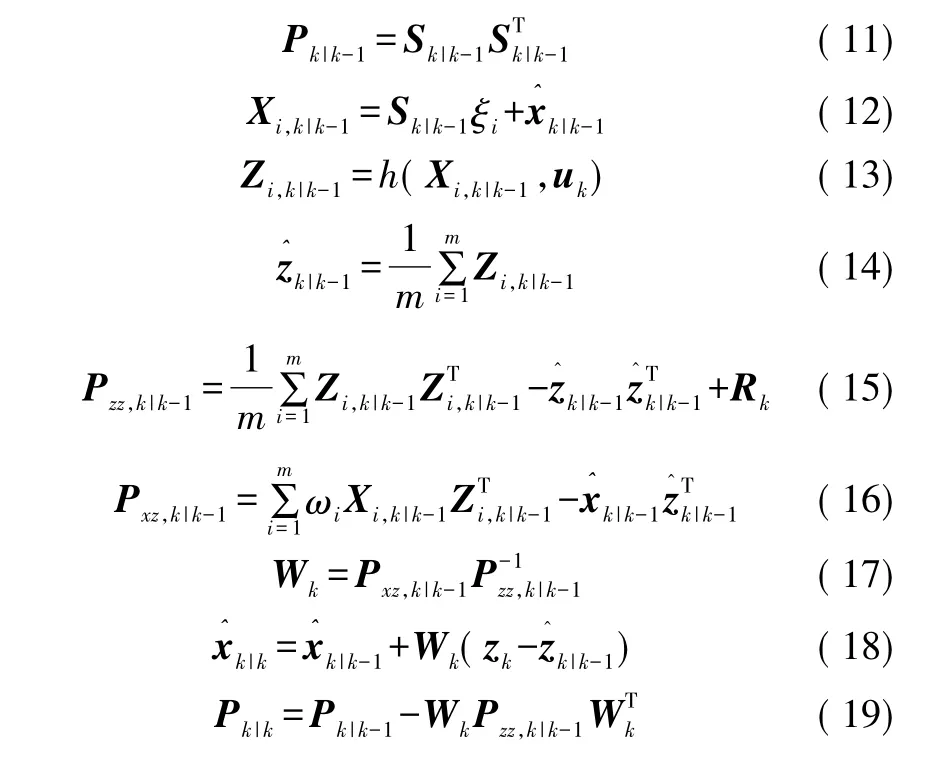
1.2 容积粒子滤波算法

令xk是均值为、方差为Pk、服从高斯分布函数N(xk;，Pk)的随机变量，p(xk)为状态 xk的概率分布，p(zk|xi

k)为似然函数，借鉴文献［5］～［8］中关于CPF算法的框架结构，得到CPF的算法流程如下。

①初始化

当k=0时，从初始状态分布p(x0)中抽取N个权值为1/N、方差为P0的粒子集。

②重要性采样

⑤输出k时刻的状态估计和方差估计

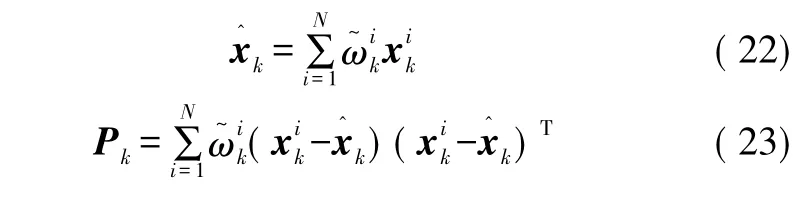
2 SINS/GPS紧耦合系统数学模型

SINS/GPS紧耦合系统结构如图1所示。组合导航系统的滤波器接收GPS跟踪回路提供的伪距和伪距率的测量值，用于生成SINS中的误差估计;修正后的SINS数据用于辅助GPS跟踪回路，实现对系统的开环校正或反馈校正;最后将组合导航系统的导航数据输入到需要实现导航定位的实际系统中。

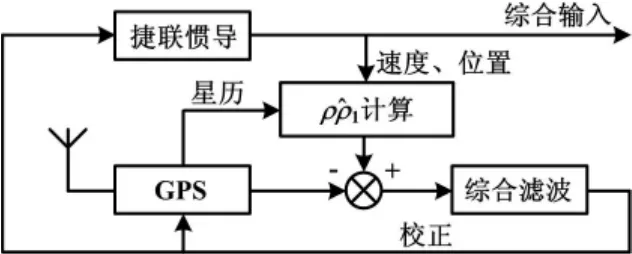
图1 系统结构框图Fig.1 Structure of the system

图1中，综合输入是指组合导航系统将GPS与SINS的导航数据综合以后的数据输入到需要实现导航定位的实际系统中。

2.1 状态方程

本文采用的数学模型建立在东北天地理坐标系的基础上，以陀螺仪加速度计和GPS接收机的各种误差为状态变量，GPS/SINS 组合系统的状态方程［1，9］为:

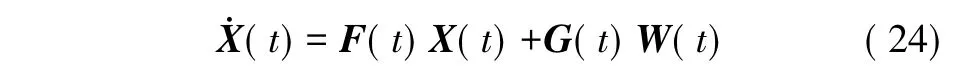
式中:X(t)∈R20为状态变量;F(t)∈R20×20为系统状态系数矩阵;W(t)∈R11为噪声向量;G(t)∈R20×11为系统噪声矩阵。

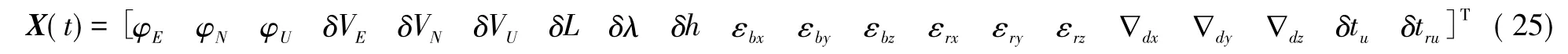
式中:φE、φN、φU为平台误差角;δVE、δVN、δVU为速度误差;δL、δλ、δh 为位置误差;εbx、εby、εbz为陀螺随机漂移;εrx、εry、εrz为一阶马尔可夫过程随机噪声;▽dx、▽dy、▽dz为加速度计随机偏差;δtu和δtru为GPS等效时钟误差相应的距离误差和距离率误差。

F(t)20×20的表达式为:

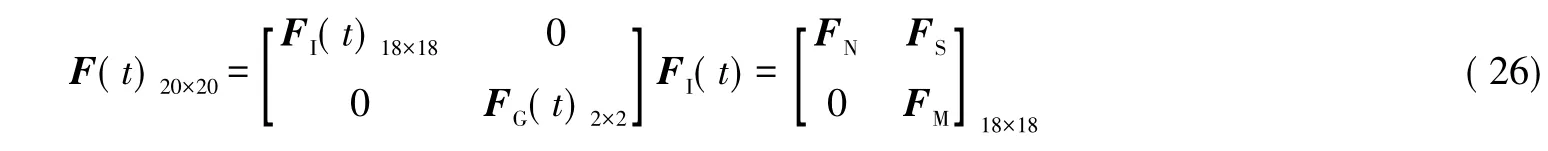
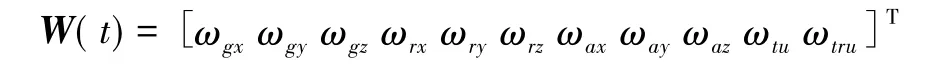
式中:ωg为陀螺仪白噪声漂移;ωa为加速度计白噪声漂移;ωr为陀螺仪一阶马尔可夫驱动白噪声;ωtu为等效时钟误差对应的距离误差;ωtru为等效时钟频率误差对应的速度误差。

2.2 量测方程

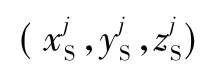
①利用SINS与GPS伪距差组成测量方程

令ρI为由SINS提供的载体位置与卫星之间的伪距，ρG为GPS接收机给出的载体位置与卫星之间的伪距，则载体上的GPS接收机相对于第j个卫星的伪距可表示为:

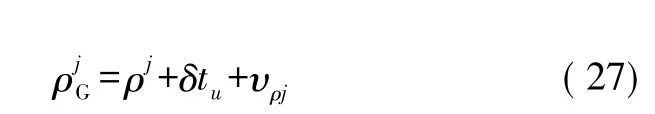
式中:δtu为等效时钟误差和卫星星历误差对应的距离率误差;υρj为伪距测量噪声，它由多路径效应、相对论效应、大气层延迟和接收机噪声等引起。

ρ与ρI由以下公式计算得到:

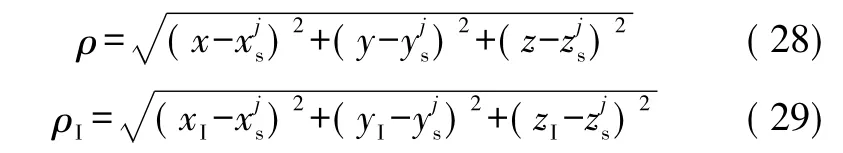
设(δx，δy，δz)为 SINS 解算出的载体在地球坐标系中的位置误差，则 xI=x+δx、yI=y+δy、zI=z+δz。

将式(29)在(x，y，z)处进行泰勒展开，并忽略二阶以上高阶项，可以得到:

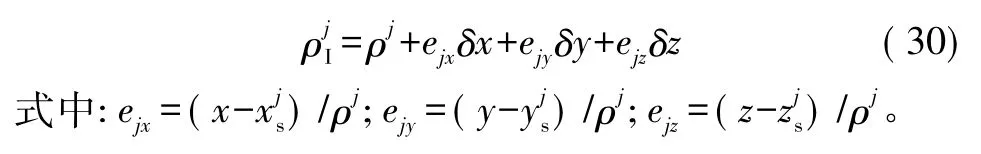
组合系统的伪距差测量方程为:

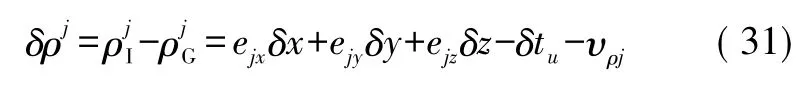
②利用SINS与GPS伪距率差组成测量方程

SINS提供的载体位置与卫星之间的伪距变化率可表示为:

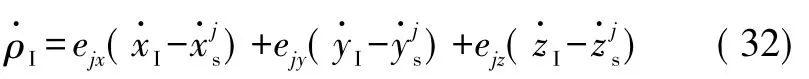
整理可得:

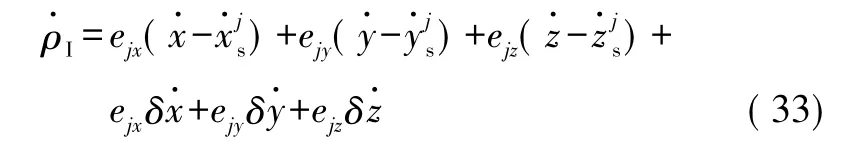
载体上的GPS接收机相对于第j个卫星的伪距率可表示为:

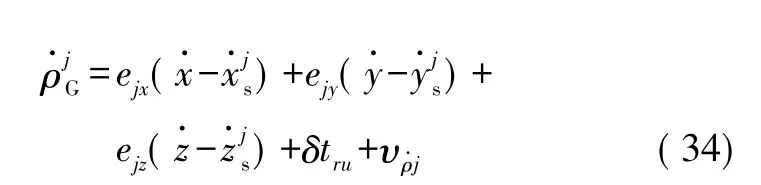
式中:δtru为GPS时钟频率误差等效的距离率误差;υρ·j为伪距率量测噪声。

组合系统伪距率差测量方程为:

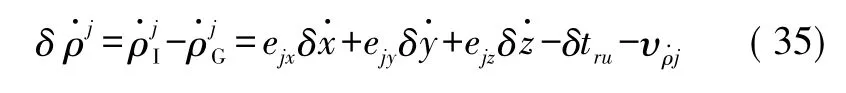
3 仿真试验分析

为验证CPF算法在SINS/GPS紧耦合导航系统中的滤波效果，利用Matlab软件进行仿真试验。仿真系统主要由轨迹发生器、SINS仿真子系统、GPS仿真子系统和CPF组合导航滤波器4部分组成。

设仿真航迹由平飞、转弯、加速和爬升等状态组成，设定载体初始位置(纬度20°、经度110°、高度500 m)，仿真时间为1 600 s，则载体飞行航迹的仿真结果如图2所示。

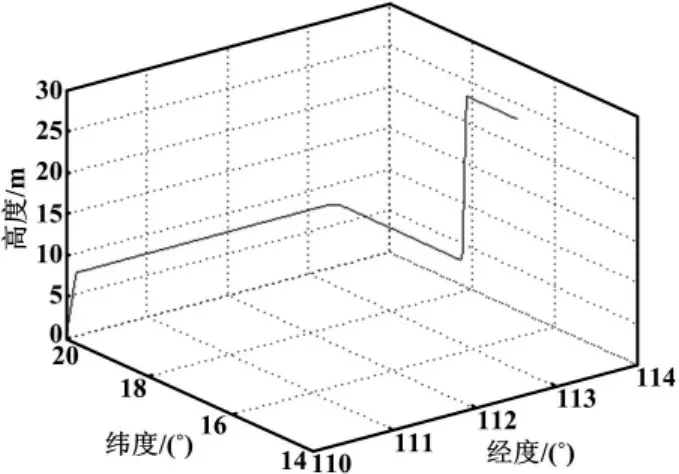
图2 载体飞行航迹三维图Fig.2 The three-dimensional graphic of carrier flight path

SINS解算频率为50 Hz，GPS接收频率为1 Hz，两者的组合频率为1 Hz。利用PF进行滤波，得到SINS/GPS导航系统的位置误差曲线如图3所示。同理，利用CPF进行滤波的位置误差曲线如图4所示。

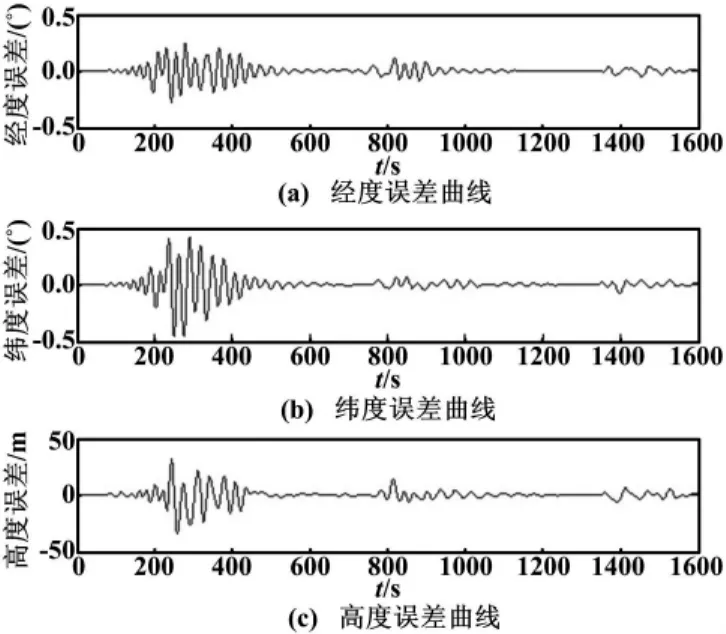
图3 组合导航PF输出位置误差曲线Fig.3 Position error curves of integrated navigation with PF

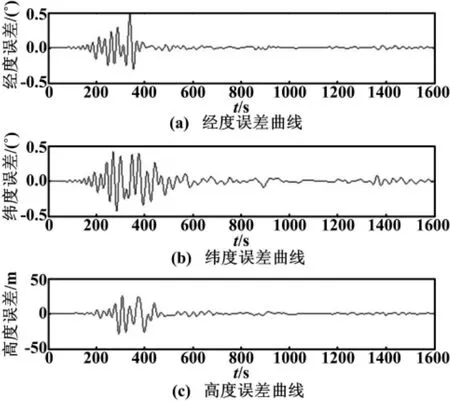
图4 组合导航CPF输出位置误差曲线Fig.4 Position error curves of integrated navigation with CPF

从图3、图4可以看出，在相同条件下，将本文采用的CPF与标准PF进行对比，可知CPF对位置的估计误差较小，且随着时间的推移，误差逐渐降低，曲线收敛于坐标轴。

仿真试验采用的位置信息是用“经纬高”来表示的，为了便于直观的对比，将图3与图4的经纬度误差转换为东北天方向的、以m为单位的误差，得到位置误差均值如表1所示。

表1 位置误差均值对比Tab.1 Comparison of the mean position errors

从表1可以看出，CPF对位置的估计值更加接近真实值，组合导航系统的定位精度显著提高。

4 结束语

本文提出将最新的非线性滤波方法CPF应用到紧耦合SINS/GPS导航系统的数据融合中，并设计了典型飞行航迹来验证其可行性与优越性。仿真结果表明，与标准PF相比，CPF利用CKF为PF提供重要性概率密度，将最新量测值融入到系统状态的转移过程中，有效克服了PF的粒子退化问题。CPF算法提高了导航系统的定位精度和滤波精度，实际效果较好。

［1］王惠南.GPS导航原理与应用［M］.北京:科学出版社，2003:207－248.

［2］ Gustafsson F，Gunnarsson F，Bergman N.Particle filters for positioning，navigation，and tracking［J］.IEEE Transactions on Signal Processing，2002，50(2):425－437.

［3］ Bouaynaya N，Qu W，Schonfeld D.An on line motion-based particle filter for head tracking applications［C］//IEEE International Conference on Acoustics，Speech，and Signal Processing，Philadelphia，USA，March，2005:225－228.

［4］ Havlicek M，Jan J，Brazdil M，et al.Nonlinear estimation of BOLD signal based on cubature particle filter［J］.Biosignal，2010(20):328－332.

［5］ Wu Weisheng，Song Chunlei，Wang Junhou，et al.Cubature Gaussian particle filter for initial alignment of strap down inertial navigation system［C］//2010 First International Conference on Pervasive Computing，Signal Processing and Applications，2010:1196－1200.

［6］ Arasaratnam I，Haykin S.Cubature Kalman filters［J］.IEEE Transactions on Automatic Control，2009，54(6):1254－1269.

［7］ Fernandez C，Vila J.Bayesian nonlinear filtering using quadrature and cubature rules applied to sensor data fusion for positioning［C］//IEEE International Conference on Communications，Cape Town，South Africa，July，2010.

［8］穆静，蔡远利，张俊敏.容积粒子滤波算法及其应用［J］.西安交通大学学报:自然科学版，2011，45(8):13－17.

［9］刘建业，曾庆化，赵伟，等.导航系统理论与应用［M］.西安:西北工业大学出版社，2010:350－355.

Application of Cubature Particle Filter in Tightly Coupled SINS/GPS Navigation System

Due to high dimensional state and nonlinear mixed model exist in data fusion of SINS/GPS tightly coupled navigation system，conventional linear Kalman filter is incompetent;while general nonlinear particle filter(PF)features particle degradation and sample depletion problems，thus the cubature particle filter(CPF)algorithm is applied in SINS/GPS integrated navigation system.With CPF，the importance density function of PF is obtained by adopting Kalman filtering algorithm，the latest measured values are integrated into the transfer process of system state;the predictive sample produced by this method is very close to real posterior probability sample of system state.The result of simulation indicates that the estimation performance of CPF algorithm is obviously better than standard PF.

Cubature particle filter(CPF) SINS/GPS integrated navigation Nonlinear system Kalman filter Data fusion

TP14

A

资助项目(编号:60974070)。

修改稿收到日期:2013－04－14。

任波(1962－)，男，1990年毕业于哈尔滨工程大学导航、制导与控制专业，获硕士学位，教授;主要从事目标探测与识别技术、信息处理与融合技术等方面的研究工作。