近断层地震激励下的隔震桥梁参数优化

马涌泉, 邱洪兴

(东南大学 土木工程学院，江苏 南京 210096)

铅芯橡胶支座(lead rubber bearing,LRB)凭借其卓越的滞回耗能特性，已在桥梁隔震领域得到了普遍应用[1-3]。近场地震动以高能量脉冲运动为特征，包含方向性效应和较大竖向加速度的特点，会使LRB隔震桥梁直接承受高能冲击，对支座位移的影响较大，其作用效应与远场地震动有着明显的不同。近年来，近断层地震动对LRB隔震桥梁响应的影响已引起学者们的高度关注[4-8]。文献[4-5]选取的LRB其硬化比(支座初始刚度与屈服后刚度的比值)在25～35。而我国生产的LRB，由于受橡胶硬度的限制，其硬化比在8～25[9]。文献[6-7]采用双线性模型模拟LRB的滞回特性，但该模型存在明显的屈服点，不能真实体现LRB的恢复力-位移间的关系。文献[8]通过单一的控制LRB屈服力来寻找使隔震桥梁地震响应与支座位移均较小的平衡点，但控制桥梁响应与支座位移的参数不仅有LRB的屈服力，还包括初始刚度和硬化比。此外，上述对LRB参数进行优化的研究仅是采用数值仿真的方式来阐述所提方法的有效性，没有开展相应的试验来验证所提方法的可靠性和准确性，致使上述科研成果缺乏可信度。

本文以四跨LRB隔震高架连续梁桥为工程背景，采用Bouc-Wen模型模拟LRB的非线性滞回特性，基于混合罚函数理论编制了用于综合优化LRB屈服力、初始刚度和硬化比的MATLAB程序，通过开展缩尺模型桥振动台台阵试验及相应的仿真分析，获得了单条和多条近断层地震激励下LRB参数的优化值，可为类似隔震桥梁的优化设计提供参考。

1 LRB参数的优化

1.1 LRB参数优化方案

Bouc-Wen双向(顺桥向和横桥向)耦合非线性滞回模型[10]能较真实地反映LRB的恢复力在水平向相耦合的特性[11]，故采用此模型来表述LRB在水平向的力学特性。选取LRB的屈服力Fy、初始刚度kb和硬化比η为待优化的参数，通过优化使得支座和梁体位移在满足容许值的前提下，能最大限度的抑制各墩底部的剪力和弯矩。定义目标函数为：

(1)

式中：pk(x,t)、pk(y,t)、fk(x,t)和fk(y,t)分别定义为：

(2)

定义约束条件为：

(3)

(4)

(5)

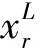
(6)

1.2 参数优化程序的编制

编制了基于混合罚函数理论的一阶优化迭代MATLAB分析程序(简称YH程序)，数学表达式为

(7)

(8)

由于上式为非线性方程，故在t～t+Δt时段内采用Newmark时间积分法求解增量形式的运动方程。t+Δt时刻的Fb可表示为：

(9)

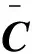
将式(9)代入t+Δt时刻的式(8)，并结合Newmark时间积分法得到：

(10)

(11)

使用四阶显式Runge-Kutta迭代法和YH程序，联合求解式(7)和式(10)，便可求得优化后的隔震桥梁地震响应和LRB最优参数。

1.3 地震激励的选取

选取如表1所示的15条近断层地震动记录作为数值仿真和振动台台阵试验所需的地震激励。

五四时期，除了本土的封建主义意识形态，附着于各种思潮的西方意识形态也涌入中国，如功利主义（实用主义）、无政府主义、基尔特社会主义、新村主义，等等，宣扬着各自对社会的见解和主张。在各种主义中，有的标榜赞成“共产主义”或“社会主义”，但其内容和实质却是伪社会主义或反马克思主义的，一时让人难辨真假，阻碍着马克思主义的科学社会主义的传播。马克思主义与一些反马克思主义的意识形态进行了较长时间的论战，比较著名的是与功利主义（实用主义）、基尔特社会主义、无政府主义的论争。

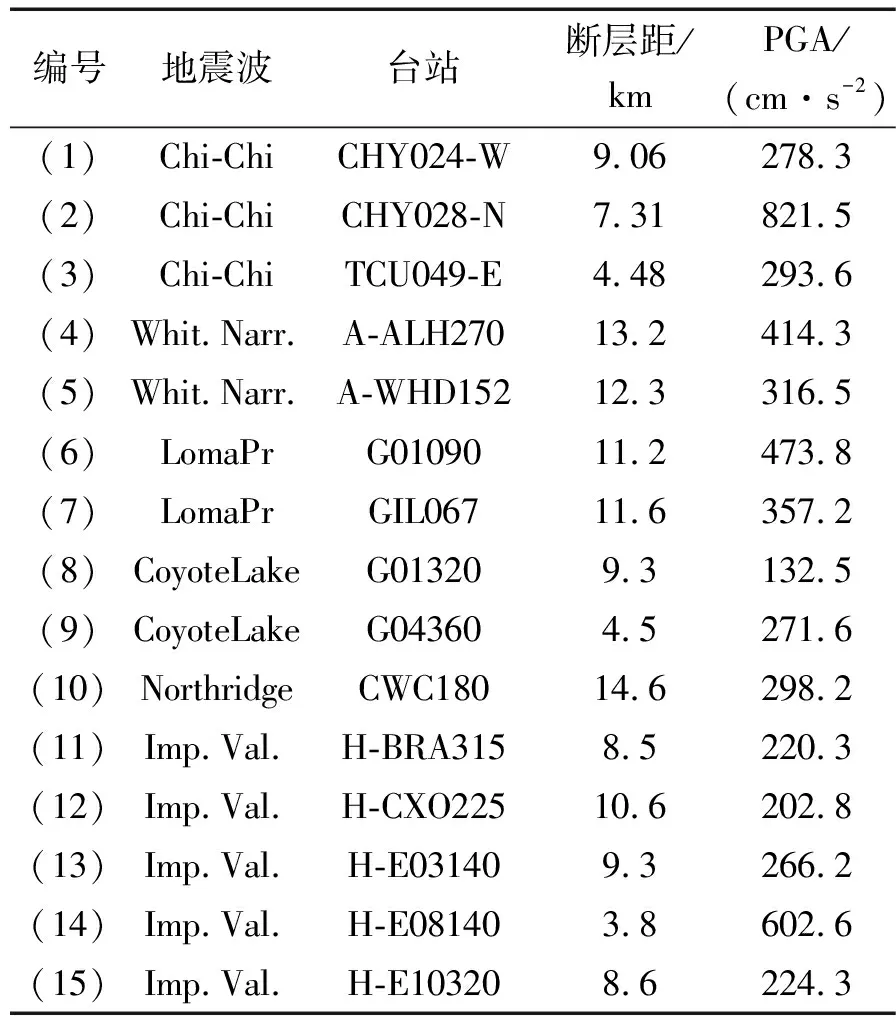
表1 近断层地震动记录

2 振动台试验

2.1 模型桥的设计及模态参数识别

选取一座四跨LRB隔震高架连续梁桥为原型桥背景，跨径布置为4×32 m，梁体采用预应力混凝土单箱双室连续箱梁，采用双柱式圆形实心钢筋混凝土桥墩。模型桥与原型桥的几何缩尺比例为1∶10，各物理量的相似性见表2。

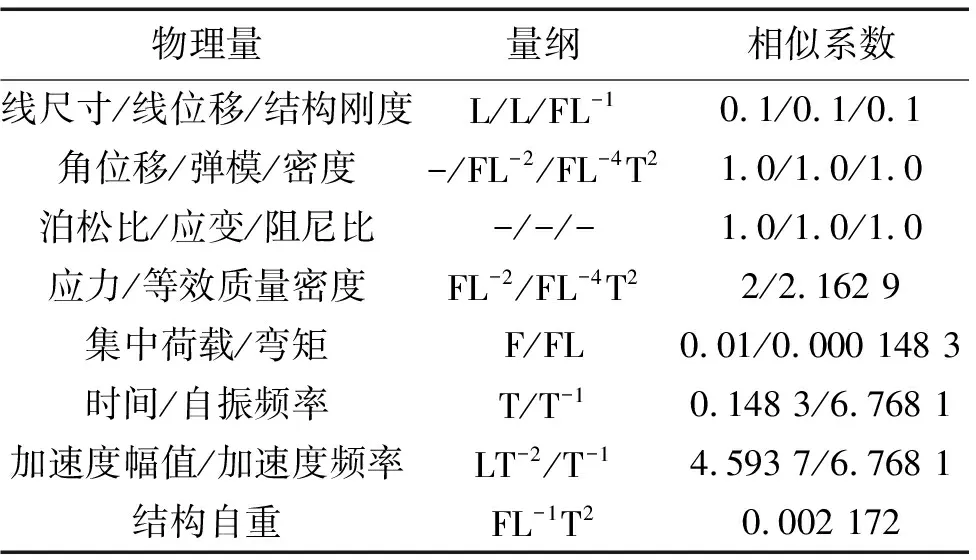
表2 各物理量的相似性

模型桥采用钢箱梁替代预应力混凝土箱梁，模型桥的桥墩形式与原型桥的相同，桥墩上部连接盖梁，下部连接承台。纵向挡块与梁端的预留间距为5 cm。承台底部固结一块3 cm厚的钢板，并将该钢板锚固在振动台上。各桥墩的纵筋均贯穿盖梁和承台，其配筋率均为3.8%，各桥墩的体积配箍率均为2.16%。钢箱梁的尺寸(单位: cm)如图1所示。

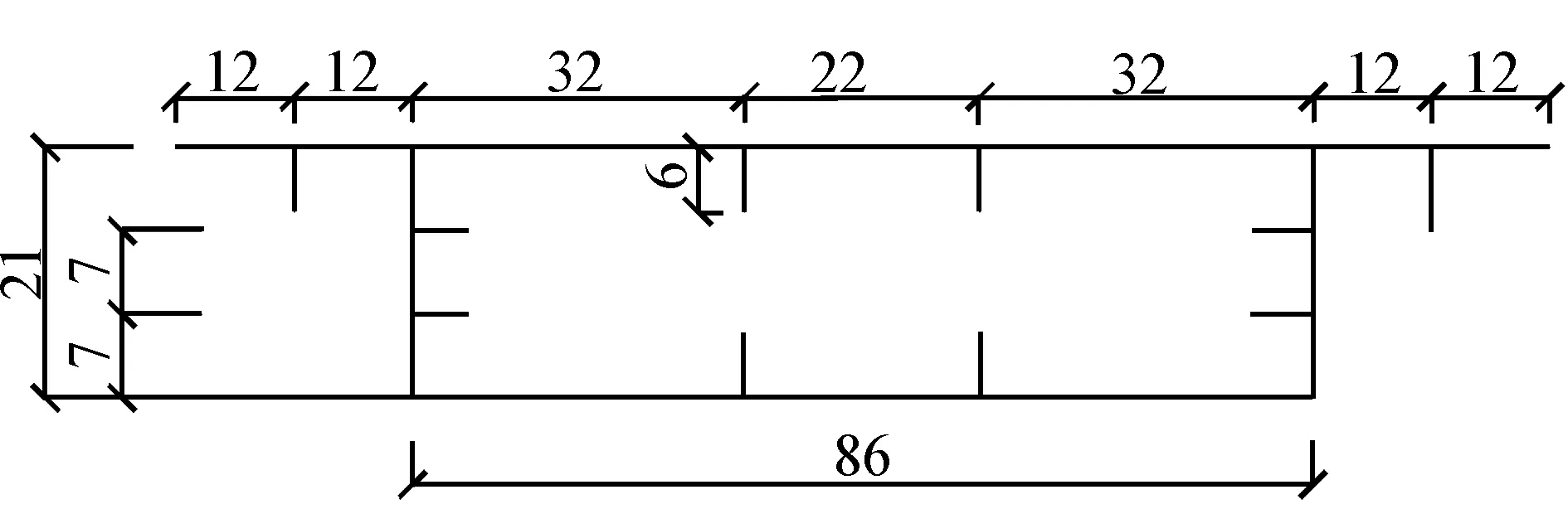
图1 模型桥钢箱梁的尺寸

在梁体的中央区布置6片重1.12 t的混凝土配重梁，在梁体两侧各布置36块混凝土实心砖。本试验在桥墩底部共布置40个应变片，用于量测在墩底可能产生塑性铰的部位的混凝土及钢筋应变；在梁体、支座、墩顶、振动台台面及墩顶-梁底等处共布置79个位移传感器，分别用于量测前四者的水平向位移和墩梁之间的相对水平向位移；在梁体、墩顶及振动台台面等处共布置39个加速度传感器，分别用于量测三者的水平向加速度；在梁端与纵向挡块之间共布置8个力传感器，用于量测梁体与边墩的碰撞力。模型桥应变片及传感器的布设位置如图2所示。分别沿模型桥的顺桥向和横桥向输入白噪声激励来识别其水平向的自振频率、振型及阻尼比。

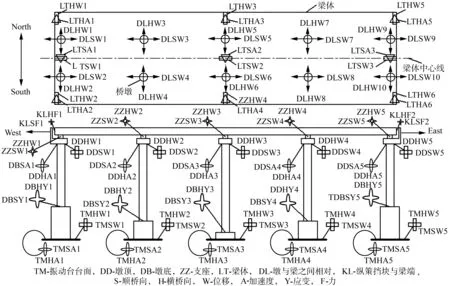
图2 模型桥应变片和传感器的布置

2.2 LRB的力学性能试验

根据静力计算得知，边墩、次边墩和中墩墩顶支座承重分别为732.7、1 162.9、1 528.6 t，中墩支座承重较大，按照中墩承重进行LRB的承载能力设计，在模型桥的每个桥墩的盖梁上布置2个LRB，全桥共布置10个LRB，各盖梁上的LRB型号相同，每个LRB的静力承重为827.6 t。经初步设计，LRB的型号选为GZY300，其构造参数见表3。

表3 GZY300型LRB的构造参数

采用500 t电液伺服试验机对LRB进行竖向压缩性能试验，见图3(a)。压力的变化范围为0.8P0～1.5P0(P0为设计压力1 005.6 kN)，加载频率范围为0.005～2 Hz(等比加载，公比为2)；采用1 000 t电液伺服压剪试验机对LRB进行水平剪切性能试验。水平位移幅值设定为±60 mm，且加载频率设定为0.05 Hz；采用500 t电液伺服试验机对LRB进行剪切性能试验，见图3(b)。通过上述3个试验得到LRB力学性能参数实测值见表4。

表4 不同轴压下的GZY300型LRB的力学参数

表中:等效阻尼比ξ为175%剪切应变下的数值；Δ为压缩变形量；kd为屈服后刚度。

(a) 压缩试验

(b) 剪切试验

通过静力计算，布置于盖梁上的LRB参数(Fy、kb和η)初始设计值分别为45.8 2kN、14.09 kN·mm-1和22.73。通过调整该支座的铅芯直径和橡胶层厚度来改变其参数，并采用上述性能试验测试调整后的支座参数直至其达到初始设计值。

2.3 LRB参数优化的试验流程

单条或多条近断层地震激励下的LRB参数优化的试验流程如图4所示。

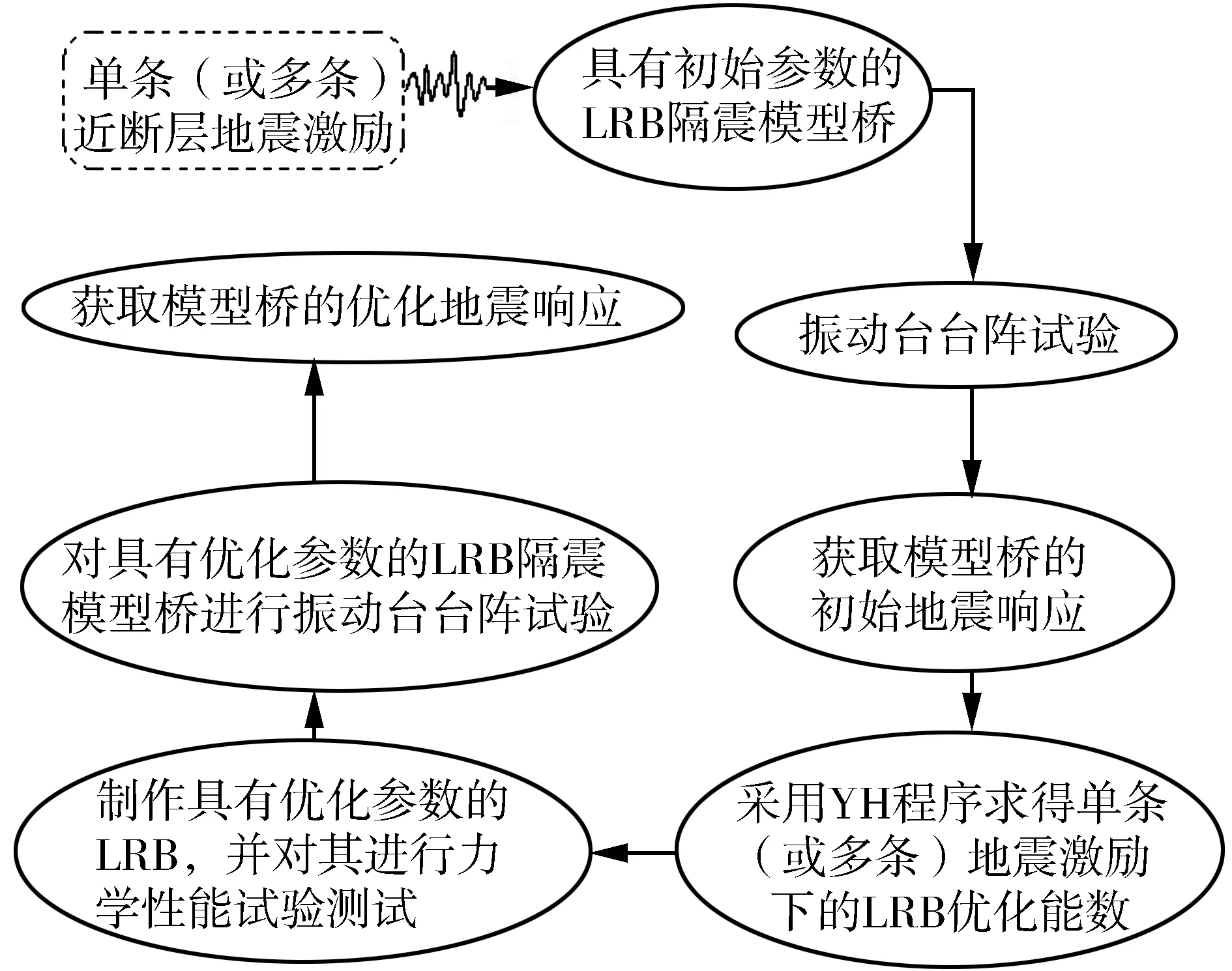
图4 LRB参数优化的试验流程

3 数值仿真

3.1 模型桥的有限元模型

本文采用有限元软件ANSYS建立了模型桥的三维精细有限元模型，如图5所示。该有限元模型的材料参数选取模型桥的实测结果，见表5。

图5 模型桥的三维有限元模型

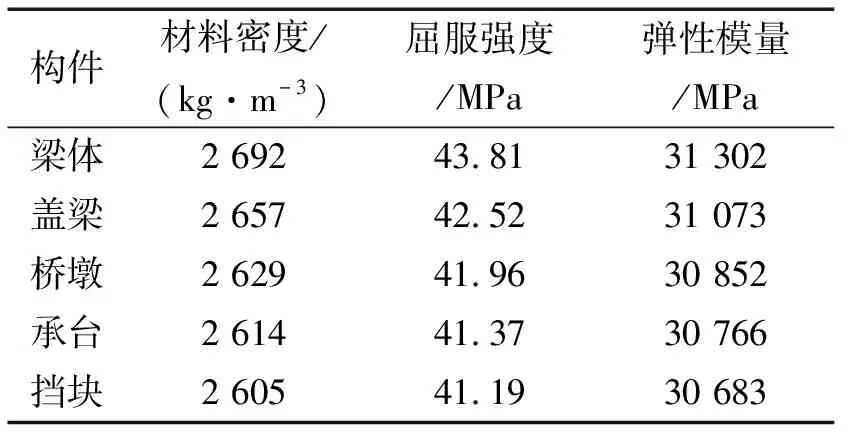
表5 有限元模型材料参数取值

由表6可以看出，对于模型桥的模态有限元计算值与测试值，两者的振动频率非常接近，两者的振型特征也完全一致，且前3阶振型均表现出水平隔震的效果，进而验证了所建立的有限元模型的正确性，表明该模型能真实反映模型桥的动力特性。

表6 模型桥模态的有限元计算值与实测值对比

3.2 LRB参数优化的仿真流程

单条或多条近断层地震激励下的LRB参数优化的仿真流程如图6所示。

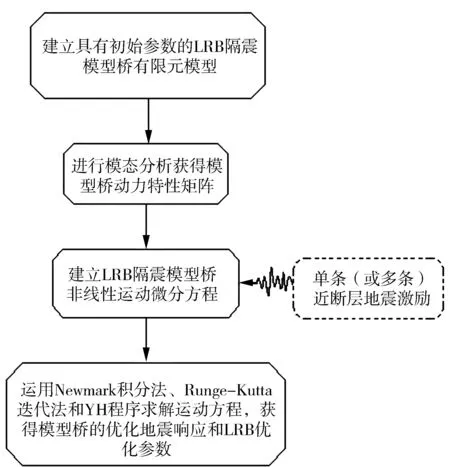
图6 LRB参数优化的仿真流程

4 结果分析

4.1 单条地震激励的优化

模型桥的抗震设防烈度为8°，故按照《公路桥梁抗震设计细则》[12]的规定要将15条近断层地震动记录的PGA统一调至0.25 g。梁体与支座在水平向(顺桥向和横桥向)的位移限值均为5.00 cm，墩与梁之间的水平向相对位移限值为4 cm。未隔震桥采用刚性铰支座，其位移限值为3 cm。对模型桥进行在单条地震激励下的振动台台阵试验获得试验值，采用Newmark法、Runge-Kutta法和YH程序求解单条地震激励下的模型桥运动方程获得仿真值。(11)号地震激励下的模型桥各项评价指标的试验值和仿真值见表7。条地震激励下的优化参数为：Fy=39.86 kN，kb=12.25 kN·mm-1，η=19.77

由表7可知，无论是初始响应还是优化响应，其试验值与仿真值均非常接近；刚性铰支座位移有一部分已超出限值，隔震模型桥的梁体及支座位移的初始响应均较大，且均已超出限值。参数优化后的梁体及支座位移均得到显著降低。优化后的墩顶位移和梁体加速度也均比优化前有了显著降低；优化后的墩底剪力和墩底弯矩虽比优化前有了一定的增大，但增大幅度并不大；由图7可以看出，在其他单条近断层地震激励下，优化后的模型桥其梁体及支座水平向位移峰值也均在限值范围内。

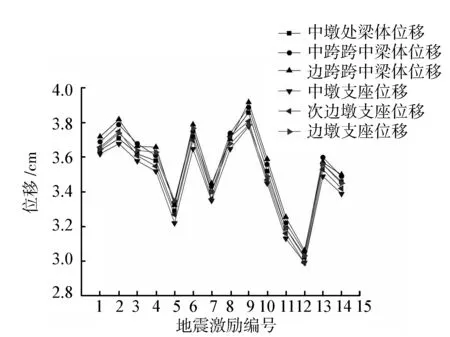
图7 梁体及支座水平向位移峰值

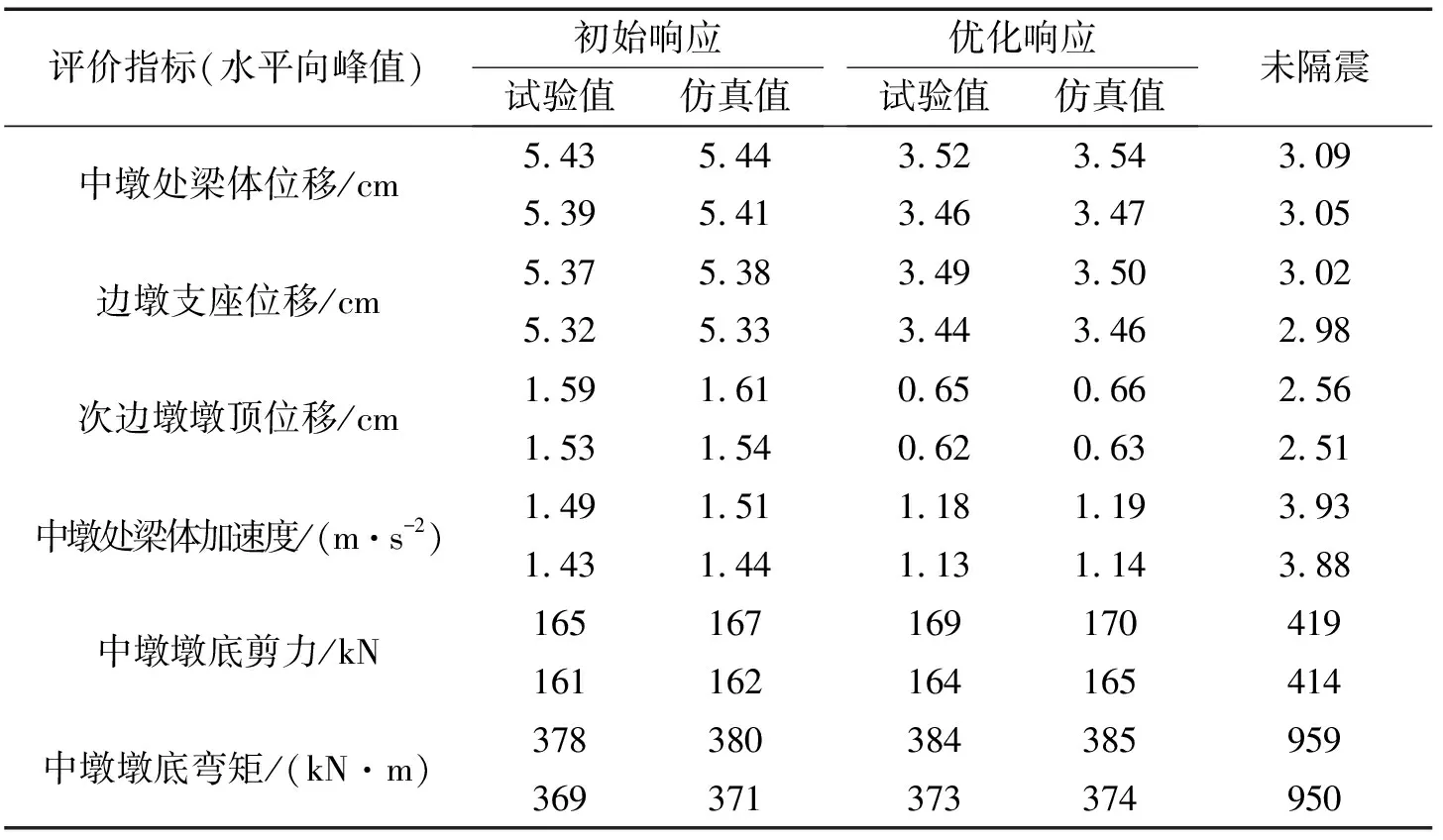
表7 (11)号地震激励下的各评价指标计算结果

4.2 多条地震激励的优化

采用YH程序对15条地震激励下的LRB参数进行优化，获得多条地震激励下的LRB优化参数A (Fy=32.7 5kN，kb=11.82 kN·mm-1和η=18.63)，运用Newmark法和Runge-Kutta法求解具有优化参数A的隔震桥在单条地震激励下的运动方程，获得多条优化响应A；采用YH程序仅对某一条地震激励下的LRB参数进行优化，获得该条激励下的LRB优化参数B，运用Newmark法和Runge-Kutta法求解具有优化参数B的隔震桥在该条激励下的运动方程，获得单条优化响应B。两者的计算结果见表8。

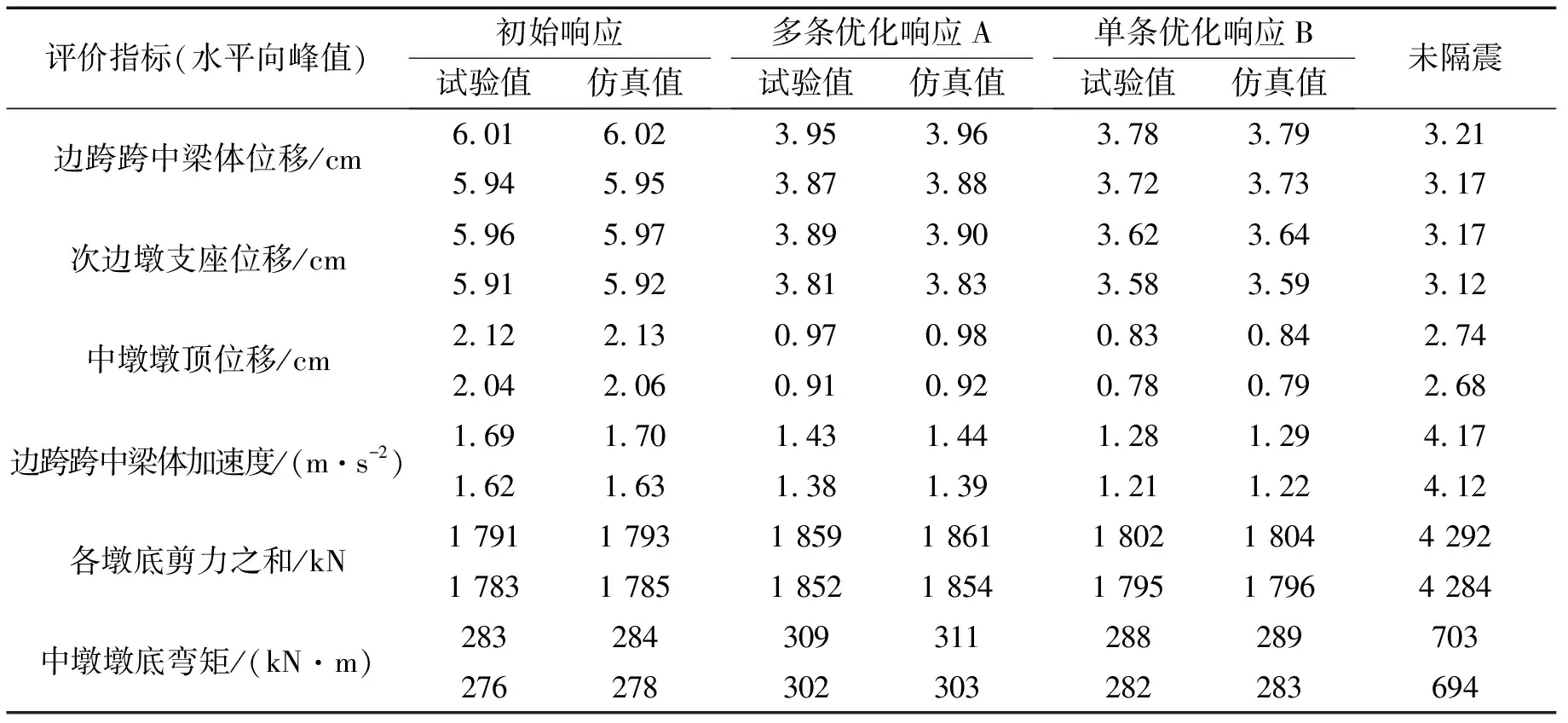
表8 多条或(8)号地震激励下的各评价指标计算结果

由表8可知，无论是多条优化响应A还是单条优化响应B，其试验值与仿真值均非常接近；多条优化响应A和单条优化响应B的梁体位移、支座位移、墩顶位移和梁体加速度峰值均比初始响应的有了显著降低；多条优化响应A和单条优化响应B的墩底内力峰值比初始响应的都有所增大，其中单条优化响应B的增幅不太显著，而多条优化响应A的增幅较明显；多条优化响应A的YH程序目标函数值(各墩底剪力之和、各墩底弯矩之和)要大于单条优化响应B的目标函数值。

图8 目标函数增大率

由图8可以看出，在其他单条地震激励下，按照多条优化参数算得的目标函数值比初始参数算得的有所增大，但增大率最大值也仅为5.51%。由图9可以看出，在其他单条地震激励下，多条优化响应A的梁体及支座水平向位移峰值也均在限值范围内。可见，采用多条地震激励下的优化参数(运用YH程序对目前已知的多条地震激励下的LRB进行优化所获得的参数)用于桥梁的隔震优化设计，在面对不确定的地震激励时，仍能控制梁体及支座的位移在限值内，并且不会引起目标函数值的显著增大。

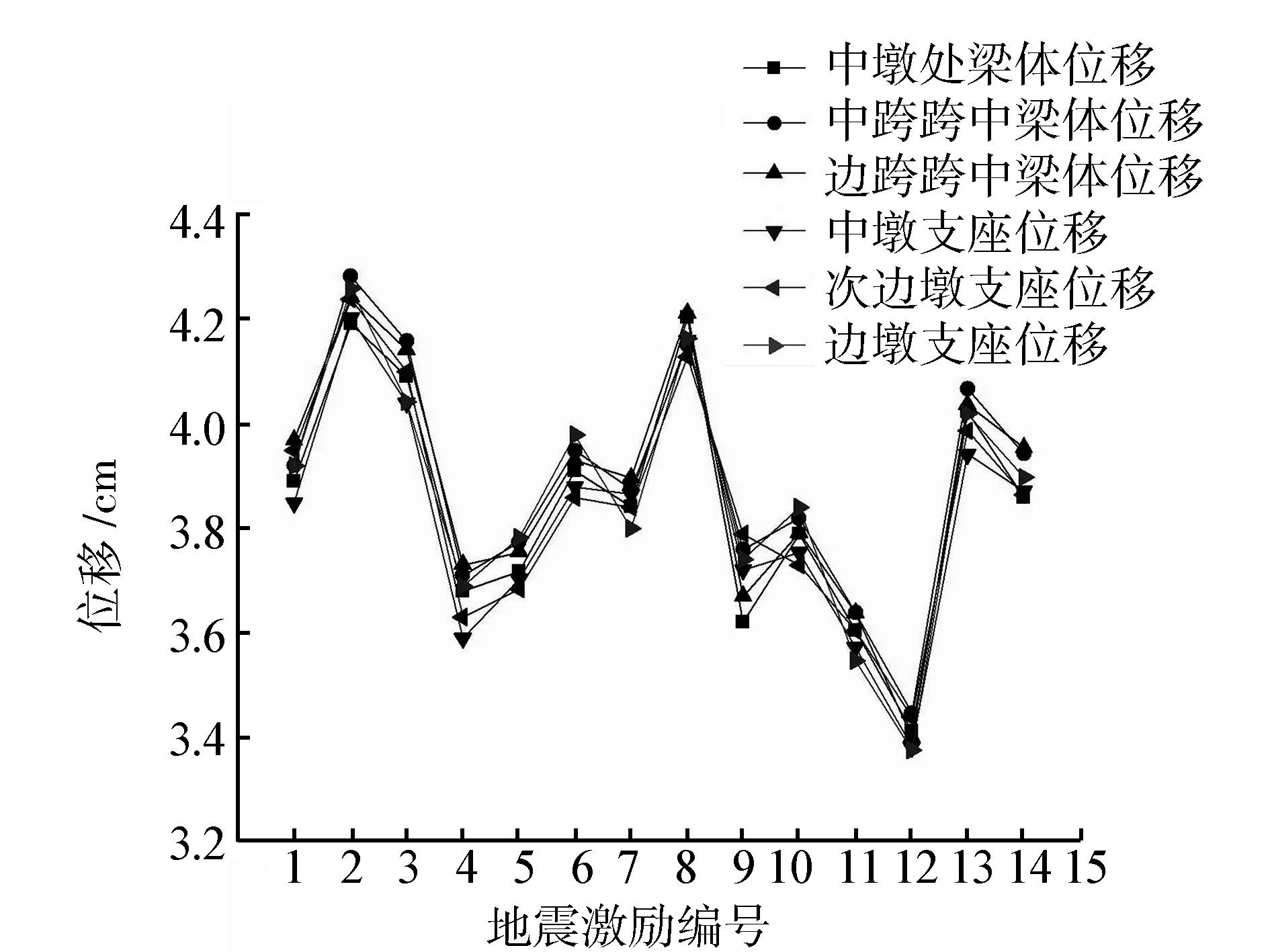
图9 由优化参数A计算出的梁体及支座水平向位移峰值

5 结论

1) 在单条或多条近断层地震激励下，LRB隔震模型桥在优化前后的水平向地震响应的仿真值与试验值都非常接近；在单条或多条近断层地震激励下，优化后的隔震模型桥其梁体及支座水平向位移峰值均在限值范围内。

2) 单条近断层地震激励下的目标函数值比多条近断层地震激励下的要略小一些；后者比初始的目标函数值要有所增大，但增大率的最大值仅为5.51%；使用YH程序获得的多条近断层地震激励下的LRB优化参数可用于未知地震激励下的桥梁隔震设计。

参考文献：

[1]KUNDE M C, JANGID R S. Seismic behavior of isolated bridges: a-state-of-the-art review[J]. Electronic Journal of Structural Engineering, 2003, 3(2): 140-169.

[2]PAUL D K. Force-deformation behavior of isolation bearings[J]. Journal of Bridge Engineering, 2007, 12(4): 527-529.

[3]HAMEED A, KOO M S, DAI D T, et al. Effect of lead rubber bearing characteristics on the response of seismic-isolated bridges[J]. KSCE Journal of Civil Engineering, 2008, 12(3): 187-196.

[4]DICLELI M, BUDDARAM S. Effect of isolator and ground motion characteristics on the performance of seismic-isolated bridges[J]. Earthquake Engineering and Structural Dynamics, 2006, 35(2): 233-250.

[5]JANGID R S. Optimum lead-rubber isolation bearings for near-fault motions[J]. Engineering Structures, 2007, 29(10): 2503-2513.

[6]PARK K S, JUNG H J, LEE I W. A comparative study on aseismic performances of base isolation systems for multi-span continuous bridge[J]. Engineering Structures, 2002, 24(8): 1001-1013.

[7]SHEN J, TSAI M H, CHANG K C, et al. Performance of a seismically isolated bridge under near-fault earthquake ground motions[J]. Journal of Structural Engineering, 2004, 130(6): 861-868.

[8]李黎, 胡紫东, 聂肃非, 等. 基于近断层地震LRB桥梁支座屈服力优化[J]. 振动与冲击, 2011, 30(6): 134-138.

LI Li, HU Zidong, NIE Sufei, et al. Optimum yield strength of LRB for isolated bridges under near-fault earthquake[J]. Journal of Vibration and Shock, 2011, 30(6): 134-138.

[9]陈水生, 马涌泉. 基于MRD与LRB混合控制的隔震连续梁桥地震响应[J]. 北京工业大学学报, 2013, 39(3): 378-384.

CHEN Shuisheng, MA Yongquan. Seismic responses of isolated continuous girder bridges based on hybrid control of MRD and LRB[J]. Journal of Beijing University of Technology, 2013, 39(3): 378-384.

[10]PARK Y J, WEN Y K, ANG A S. Random vibration of hysteretic systems under bi-directional ground motions[J]. Earthquake Engineering and Structural Dynamics, 1986, 14(4): 543-557.

[11]HUANG W H, FENVES G L, WHITTAKER A S, et al. Characterization of seismic isolation bearings for bridges from bi-directional testing[C]//Proceedings of the 12th World Conference on Earthquake Engineering. Auckland, New Zealand,2000: 2047-2054.

[12]中华人民共和国交通运输部. JTG/T B02-01-2008, 公路桥梁抗震设计细则[S]. 北京: 人民交通出版社, 2008.