具有输入与状态时变时滞线性系统的鲁棒H∞控制

侯晓丽 ,邵诚,李永凤

(1.郑州轻工业学院 数学与信息科学系,河南 郑州 450002；2.大连理工大学 电信学院,辽宁 大连 116085)

时滞现象存在于许多实际系统，如生物系统、经济系统、化工系统、物理系统，电力系统等，时滞的存在有时会导致系统不稳定，或使得系统的性能下降。近年来，对具有输入时滞和状态时滞的线性系统的鲁棒控制及H∞控制已有大量的研究成果[1-10]，其中很多文献要求系统是能控的且时滞依赖的结果大都要求时滞的导数小于1,但在很多实际系统中,可能无法预知时滞参数导数的情况, 如遥操作系统和网络控制系统中的时滞参数变化很快, 有时时滞参数的导数甚至可能不存在, 这时已有方法就不适用了。有的结果对时滞导数没有限制，如郑敏等[11]对一类状态及输入具有区间变时滞的线性系统，基于时滞划分形式的泛函，讨论系统的镇定问题；王新梅等[12]利用一个积分等式，给出了一类区间时变输入时滞与状态时滞线性系统的时滞相关稳定性判据等，但结果有一定的保守性。

对没有不确定性和外扰的系统，结合自由权矩阵技巧，不经过任何不等式放缩，利用Lyapunov稳定性定理，得到了系统渐近稳定的时滞依赖充分性条件，且对时滞的导数没有任何限制，解决了稳定性问题中保守性产生的根源。然后把该方法用于不确定系统，研究其鲁棒控制与H∞控制。

1 系统描述及主要结果

考虑具有如下形式的不确定时滞系统：

(1)

假设参数不确定性为范数有界的，即存在适当维数的常值矩阵E、G1、G2、G3、G4，使得

式中：F(t)∈Ri×j为未知的时变函数矩阵，其元素为可测的且满足FT(t)F(t)≤I∀t。

引理[10]假定存在适当维数的相容矩阵M、N和正定对称矩阵R、Q，对任意满足FTF≤R的F有Q+MFN+NTFTMT<0成立等价于存在标量λ>0使得Q+λMMT+λ-1NTRN<0成立。

目的是设计状态反馈控制器u(t)=Kx(t)，使得从外部扰动输入ω(t)到被调输出z(t)的传递函数Tωz小于给定的正数γ。

先考虑没有不确定性的系统：

(2)

定理1 对系统(2)，在状态反馈u(t)=Kx(t)作用下，若存在正定对称矩阵P,Qi(i=1、2、3、4)，适当维数的相容矩阵Ni(i=1、2、3、4)和Mi(i=1、2、3)，使得下述不等式成立，则其是渐近稳定的:

(9)

其中，

证明：把状态反馈u(t)=Kx(t)代入系统(2)可得

取泛函:

则对V沿系统(2)对t求导，得

ri)Qix(t-ri)=2xTP(A0+B1K)x(t)+

2xTPA1x(t-τ1(t))+2xTPB2Kx(t-τ2(t))+

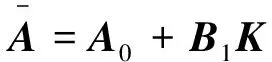
令

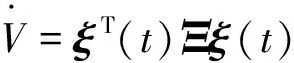
由Lyapunov稳定性定理知，系统是渐近稳定的。证毕。

整个证明过程可以看到没有任何不等式放缩，所以结果没有任何保守性。对时滞的导数没有任何限制，适合快变与慢变系统,且结果是时滞依赖的，与时变时滞的上下界有关。

对添加等式中的项数可根据需要而定。比如若系统中没有时滞项，则添加等式的方括号中可只选第一项和最后一项，其他项可以不要。

对含有不确定性的系统

(3)

同理可得下面的定理。

定理2 对系统(3)，在状态反馈u(t)=Kx(t)作用下，若存在正定对称矩阵P,Qi(i=1,2,3,4)，适当维数的相容矩阵N0和Mi(i=1,2,3)，以及正数εi、ai、bi、ci、di(i=1,2,3,4)，使得下述不等式成立，则系统(3)是渐近稳定的:

其中,

证明：与定理1的证明类似，添加等式:

令

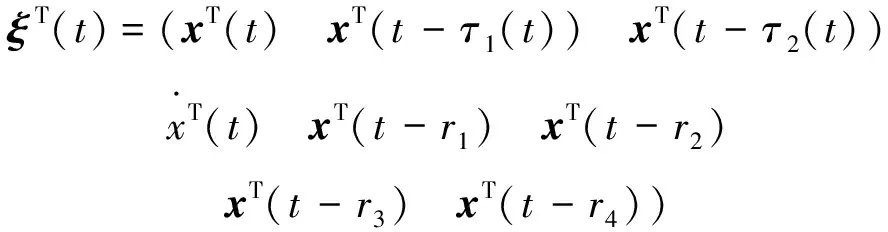
由引理1，结论即可得证。

下面考虑不确定时滞系统的H∞控制：

定理3 对系统(1)，在状态反馈u(t)=Kx(t)作用下，若存在正定对称矩阵P,Qi(i=1,2,3,4)，适当维数的相容矩阵N0和Mi(i=1,2,3)，以及正数εi,ai,bi,ci,di(i=1,2,3,4)，使得下述不等式成立:

T=

则系统(1)渐近稳定，且从外部扰动输入ω(t)到被调输出z(t)的传递函数Tωz小于给定的正数γ。其中,

2 数值算例

例1 考虑如下系统:

其中，

可见定理1的方法所得结果更好。

例2 考虑线性不确定时滞系统:

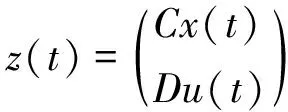
其中,

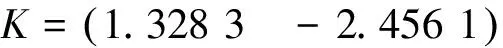
表1 性能指标与控制增益与其他文献对比结果

3 结束语

利用自由权矩阵技巧，研究了具有时变输入时滞与状态时滞的不确定系统的鲁棒H∞控制，所得结果是时滞依赖的，与时变时滞的上下界有关。从定理1的证明可以看出，没有任何不等式的放缩，所以定理1的结果没有任何保守性,且所设计的Lyapunov泛函简单，对时滞的导数也没有限制。

参考文献：

[1]CHOI H H, CHUNG M J. Memory less stabilization of uncertain dynamic systems with time varying delayed state and control[J]. Automatic, 1995, 31(9): 1349-1351.

[2]KIM J H, JEUNG E T, PARK H B. Robust control for parameter uncertain delay systems in state and control input[J]. Automatic, 1996, 32(9): 1337-1339.

[3]HAN Q L, MEHDI D. Comments on robust control for parameter uncertain delay systems in state and control input[J]. Automatic, 1998, 32(12) : 1665-1666.

[4]LEE Y S, MOON Y S, KWON W H. Delay dependent robust H∞control for uncertain systems with a state delay[J]. Automatic, 2004, 40:65-72.

[5]FRIDMAN U A.Descriptor system approach to H∞control of linear time delay system[J].IEEE Transactions on Automatic control,2002, 47: 253-270.

[6]李永钊,吴保卫.带状态时滞和输入时滞的非线性系统的鲁棒H∞控制[J].河南师范大学学报,2010,38(2):2-7.

LI Yongzhao, WU Baowei. Robust H∞control for nonlinear system with input time delay and state delay[J].Journal of Henan Normal University,2010,38(2):2-7.

[7]ZHOU Shaosheng, WEI Xingzheng. Robust H∞control of delayed singular systems with linear fractional parametric uncertainties[J].Journal of the Franklin Institute, 2009, 346: 147-158.

[8]FANG Wei. Delay dependent robust H∞control f or uncertain singular systems with state delay[J].Act Automatic Sinica, 2009, 35: 65-70.

[9]ZHANG Xianming, HAN Qinglong. Robust H∞filtering for a class of uncertain linear systems with time varying delay[J]. Automatica,2008, 44: 157-166.

[10]FRIDAM E, SHAKED U. Delay dependent stability and H∞control: Constant and time varying delays[J].Int J of Control, 2003, 76(9) : 48-60.

[11]郑敏,费树岷.一类状态及输入均有区间变时滞的线性系统之镇定[J].控制理论与应用,2008,25(5):956-958.

ZHENG Min, FEI Shumin. Stabilization for linear system with input time delay and state delay[J].Control Theory and Application, 2008,25(5):956-958.

[12]王新梅,裴海龙.一类区间时变输入时滞与状态时滞线性系统的稳定性研究[J].控制与决策,2009,24(10):1549-1554.

WANG Xinmei,PEI Hailong. Stability research for linear system with input time delay and state delay[J]. Control and Decision, 2009,24(10):1549-1554.