基于传递矩阵法和拼装角偏差的顶推梁体无应力线形的实现
2023-08-18崔立恒宋涛连光炜郭志豪陈平达
崔立恒,宋涛,连光炜,郭志豪,陈平达
1.山东省公路桥梁建设集团有限公司,山东 济南 250021;2.山东交通学院交通土建工程学院,山东 济南 250357
0 引言
桥梁工程中顶推施工速度较快,设备简单,噪声低,在预应力钢筋混凝土等截面连续梁桥和斜拉桥梁的施工中应用广泛[1-4]。顶推施工的关键步骤是确定梁体的拼装线形,直接决定顶推结束后的梁体成桥质量[5-8]。梁鹏等[9]以苏通长江大桥为例,讨论设计线形、成桥线形、无应力制造线形及安装线形间的关系,采用大循环迭代法和旋转坐标法求解安装线形。Sasmal等[10]采用基于传递矩阵法的顶推施工确定梁体线形。秦顺全[11]提出无应力状态法顶推施工,以无应力曲率和无应力索长作为桥梁施工的基本控制参数。李乔等[12]基于几何控制方法提出了桥梁全过程自适应施工控制系统。颜东煌等[13]基于桥梁全过程自适应无应力构形控制思想,推导考虑影响安装线形的主梁设计参数偏差、焊缝收缩差及温度影响等调整公式,及节段主梁实时放样精确定位公式。董创文等[14]提出考虑相位变化和组拼高程偏差的顶推梁体无应力线形的计算方法。李传习等[15]提出基于相位变化的顶推曲梁桥自适应无应力构形的计算方法。林建平等[16]以槽型组合梁为研究对象,提出基于传递矩阵确定梁体安装线形的方法。Sampaio等[17]将三维虚拟技术应用于桥梁顶推线形观测中。顶推梁体拼装线形以相位变化和传递矩阵等方式控制梁体拼装线形,但其存在应用不便或未能修正梁体拼装线形偏差等诸多不足。
本文提出基于传递矩阵和拼装角偏差推导顶推梁体安装高程的计算方法,以两梁体间的拼装角为控制参数,明确传递关系,即时修正梁体线形偏差,以期实现拼装线形和理论制造线形的统一。
1 基于传递矩阵法和拼装角偏差的梁体顶推线形控制
顶推施工是指在拼装平台上完成梁体拼装,再采用顶推设备将拼装梁体向前顶推一段距离,在拼装平台上完成下节段的梁段拼装。重复以上步骤,完成整个梁体的顶推。为描述方便,将未完成拼装的梁体定义为待拼梁段,已拼装完成的梁体定义为已拼梁段。
根据无应力状态理论,将待拼梁段和已拼梁段视为无应力状态[11]。为保障顶推施工质量,需保证顶推施工结束时梁体的无应力线形与理论制造无应力线形一致。在顶推过程中,已拼梁段的无应力线形不变,即在梁体拼装平台上保证梁体间的拼装角满足制造线形曲率。基于顶推施工,提出确定待拼梁段拼装高程的方法。钢梁拼装多为夜间作业,设温度场恒定,或温度场对梁体拼装的影响可忽略不计。
1.1 两相邻梁体间的传递矩阵
设有n段顶推梁,各梁段长li(i=1,2,…,n),待拼梁段高程为Hi,待拼梁段前、后高程差为ΔHi,水平倾角为θi,则两相邻梁体的夹角Δθi=θi-1-θi,在各施工阶段S,两相邻梁段的拼装示意图如图1所示。
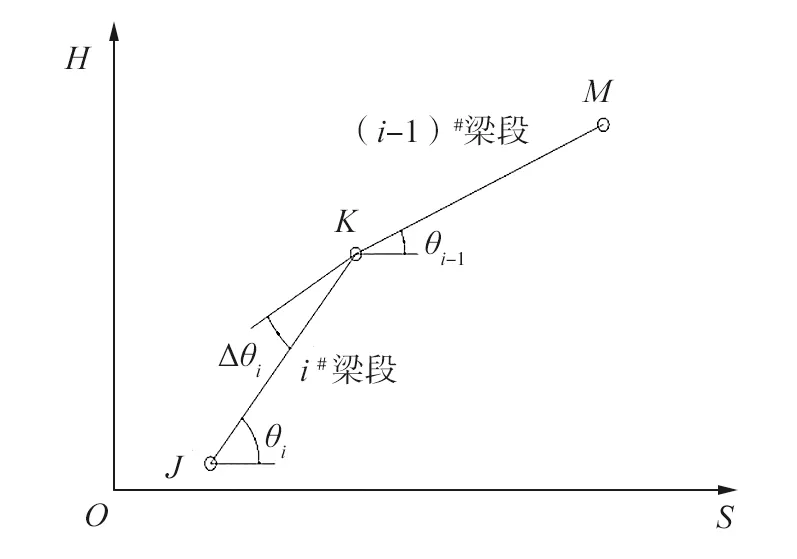
图1 两相邻梁段的拼装示意图
顶推钢梁的施工状态主要有理论无应力制造线形N、预拼装线形(用于确定钢梁理论拼装位置)C和实际拼装线形A等线形状态,可用Δθi、ΔHi和li描述梁体的线形状态,分别采用Φi-1=[Hi-1li-1]T、Φi=[Hili]T描述已拼梁段i-1和待拼梁段i的线形状态。
根据传递矩阵的概念[10],梁段i的拼装传递方程为:
Φi=TiΦi-1,

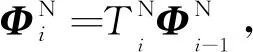
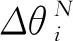
(1)
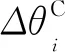
考虑梁体线形修正后梁段i的预拼装传递方程为:
(2)
1.2 1#钢梁拼装高程及拼装角偏差计算



图2 1#钢梁拼装及拼装角偏差示意图
根据几何关系,可得
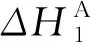

1.3 梁段i的拼装高程及梁体线形偏差
顶推(i-1)#段梁体前移一段距离后,梁体由待拼梁段变为已拼梁段。此时,梁体的无应力线形保持不变,可视为梁体随1#梁段做刚体运动。

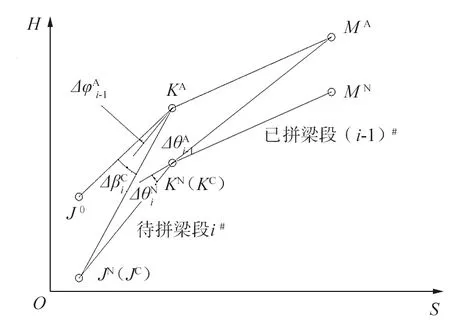
图3 待拼梁段i#拼装及拼装角偏差示意图
根据已拼梁段i#的梁体前、后梁段高程及式(1)(2)计算可得待拼梁段i#的传递方程为:

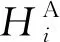
2 工程应用
2.1 工程概况
某双塔三跨矮塔斜拉桥结构为145 m+240 m+145 m,如图4所示。主梁为单箱三室钢箱梁,钢箱梁高4.80 m,宽28.50 m,桥面设有坡度为2%的横坡,底板水平,箱梁横断面如图5所示。钢箱梁全长530.00 m,有56个节段,标准节段长9.60 m,最长节段长13.00 m。采用顶推法拼装主梁,经19轮次顶推作业完成梁体拼装,顶推长462.80 m,钢导梁长45.10 m,布设5个临时墩,根据成桥标高设置墩顶标高。

单位:m。 图4 桥梁结构立面图

单位:m。 图5 箱梁横断面图
2.2 梁体理论无应力制造线形
此桥钢箱梁的无应力制造线形为变曲率竖曲线,采用矩形法确定梁体制造线形,梁体上、下焊缝宽度差如表1所示。
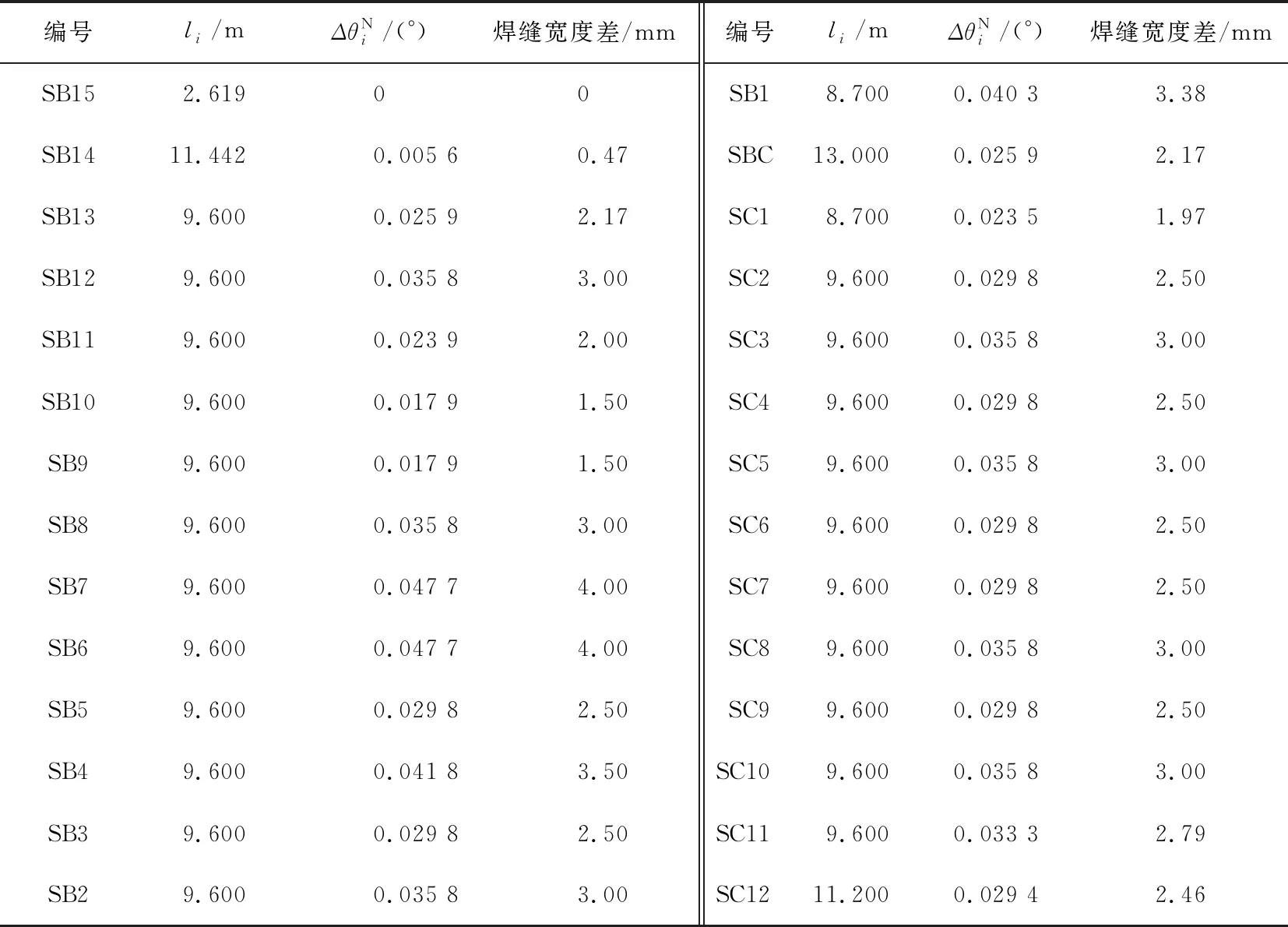
表1 典型梁段上、下焊缝宽度差
由表1可知:梁体无应力制造线形的平均焊缝宽度差约为3.00 mm,受梁体高度及现场实际条件制约,采用矩形法现场拼装梁体。
2.3 待拼梁段高程确定

可编程计算后续梁段的拼装参数,以SC8~SC11节段为例,结果如表2所示,其余梁段做类似处理。
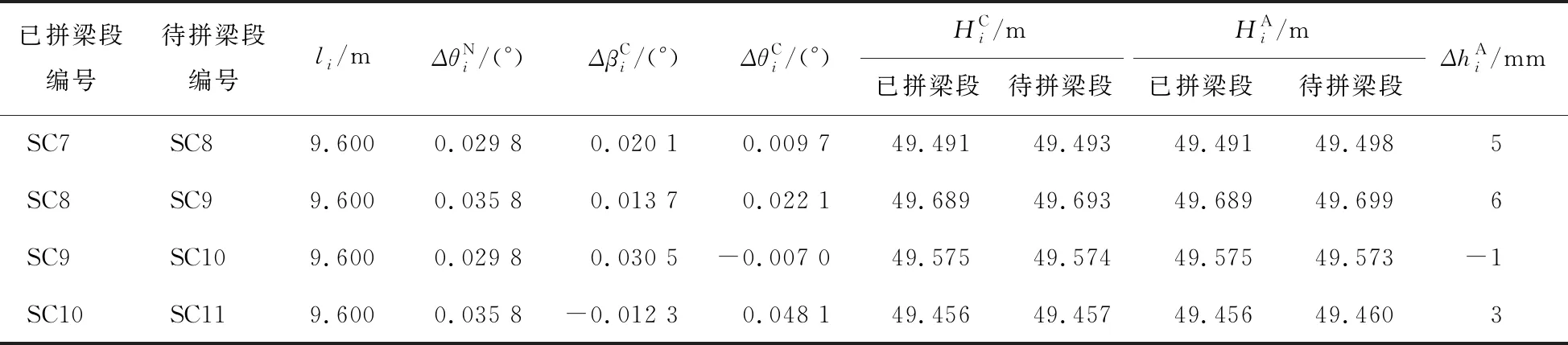
表2 SC8~SC11梁段的拼装参数
2.4 后续梁体线形控制结果
已拼梁体顶推到某一工况下,根据梁体实测线形扣除自重作用下的挠度曲线,得到梁体的无应力线形,与理论无应力线形的偏差如图6所示。由图6可知:梁体的实测无应力线形与理论无应力线形高度吻合,绝大多数测点的偏差小于10 mm,可实现梁体的高精度拼装。
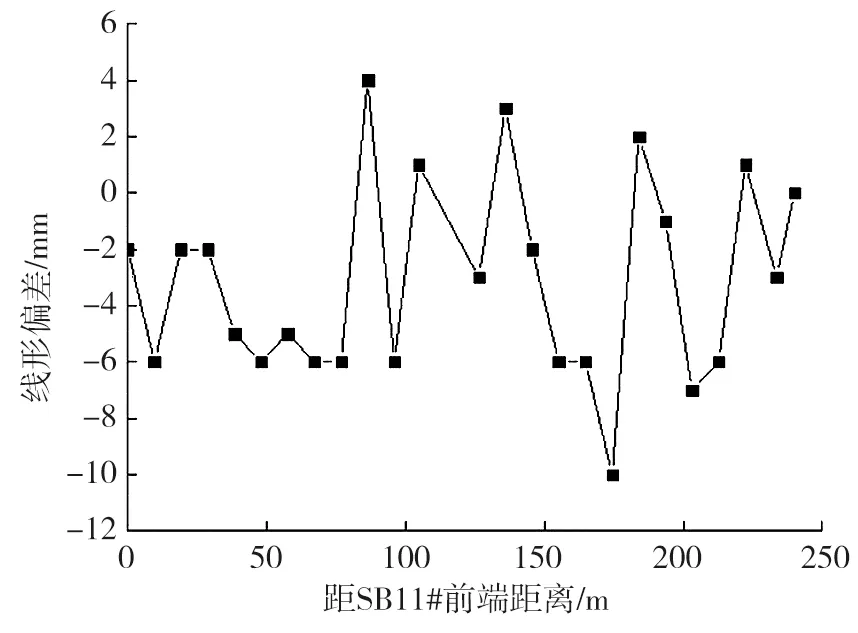
图6 某工况下梁体无应力线形与理论线形偏差
3 结束语
1)基于传递矩阵法和拼装角偏差,提出梁体拼装高程的计算方法,以拼装角及其偏差为控制量,采用传递矩阵计算梁体待拼高程,实时修正因拼装偏差、大气温度变化及焊接残余变形等引起的拼装角偏差,使梁体拼装线形与理论制造线形基本一致,采用自编程序即可计算拼装参数,简单直观。
2)顶推梁体拼装高程的计算方法可保证已拼梁体和待拼梁体间的无应力线形与梁体理论制造线形统一,保证梁体顶推结束成桥后的梁体无应力线形与理论线形统一。此方法还可用于确定大节段拼装和悬臂拼装等施工梁体线形。
上述研究基于温度恒定状态,在实际梁体拼装工作中,一般需考虑温度场的影响,下一步研究将考虑沿腹板高度方向上的温度梯度变化。
