考虑需求依赖库存及分摊运费的供应链协调
2014-09-17刘俊
刘 俊
(合肥工业大学 数学学院,安徽 合肥 230009)
1 引 言
在最近几十年里,市场研究者发现,某些产品的需求受其货架展示量的影响,商品展现常常能刺激顾客的购买欲望[1].文献[2]最早将需求受库存影响这一现象引入到库存模型中.文献[3]在需求依赖于当前库存水平的情况下,研究了产品短缺量部分延期供给及具有时变的变质率的库存模型.文献[4]考虑了需求依赖库存水平下具有非线性库存费用的EOQ模型.文献[5]进一步扩展了文献[4],允许短缺发生并且短缺量部分延期供给.文献[6]研究了需求受库存水平影响,且缺货时存在延迟订货的短生命周期物品的库存管理问题.文献[7]进一步将商品的库存分为展示区和仓库储存区,并且假设需求依赖于展示区商品的库存量.上述文献仅考虑了需求依赖于库存水平情形下,销售商处的库存控制问题.然而随着经济的发展,企业的竞争已不再是单个企业的竞争,而是企业所在的供应链之间的竞争,这使得供应链协调问题受到了广泛关注.文献[8]在需求依赖于当前库存水平的假设下,研究了单一生产商向单一销售商提供数量折扣的供应链完美协调.文献[9]针对需求依赖于初始库存水平的供应链商业信用期问题,提出了利润补偿机制以对供应链内增加的利润进行重新分配,实现供应链的协调.文献[10]在需求依赖于当前库存水平并且销售商库存容量有限的假设下,研究了供应商通过信用支付策略协调供应链的问题.文献[8]、[9]、[10]均研究了需求依赖于库存水平的供应链协调问题,但它们都没有考虑产品的运输费用.而实际上,运输费用是客观存在的,且在供应链的成本中占有很大的比例.文献[11]考虑了产品的运输成本,研究了单个生产商和单个销售商通过共同补给期和分担运输成本策略来进行供应链协调的问题,但其假定市场需求为弹性需求,而未考虑需求依赖于当前库存水平的情形.本文在文献[8]的基础上拟综合考虑需求依赖于库存水平及分担运输成本策略来进行供应链的协调研究.
本文假定需求依赖于当前库存水平,产品运输费用与订货量相关,研究了采用分摊运费策略的供应链协调问题.首先在Stackelberg博弈的框架下,得出了供需双方在分散式系统下,无法实现供应链完美协调,然后为生产商设计了一个分担运输费用的协调策略.研究结果表明该协调策略不仅能提高供需双方的利润,而且使得供应链达到了完美协调.
2 基本假定与记号
(i)假设生产商为整个供应链的主导方,他了解销售商的各项费用和市场需求,且不考虑生产商处的库存费用;
(ii)销售商一个周期内只进行一次订货且不允许缺货,其市场需求率依赖于当前库存水平,即D(t)=αI(t)β,其中α>0,0<β<1,I(t)为销售商在t时刻的库存水平;
(iii)t时刻的库存费h(t)=λ+hI(t),其中λ为单位时间的库存费用,h表示单位时间单位产品的库存费用;
(iv)Ar表示销售商每次订货的固定订货费用,Am表示生产商每次生产的准备费用,c表示生产商生产单位产品的成本,p表示销售商单位产品的销售价格,x表示销售商单位产品的运输费用,w是生产商给予销售商的单位产品的批发价格,为决策变量,并假设其不超过c+x;
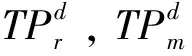
(vi)销售商接受协调策略的条件是:策略后利润比策略前高出某个百分比,L表示销售商可获得的最少利润增量的百分比.
3 模型建立与求解
根据假设,销售商在一个订货周期内库存水平变化的微分方程可表示为
dI(t)/dt=αI(t)β, 0≤t≤T.
由边界条件I(0)=Q,得
I(t)=[Q1-β-α(1-β)t]1/(1-β).
(1)
故销售商每个订货周期的长度为
T=Q1-β/[α(1-β)].
(2)
3.1 一体化供应链系统
为了得到一个基准,首先考虑生产商有自己的零售部,即一体化情形.该联合公司的利润等于销售收入减去生产成本、固定订货费用、生产准备费用、运输费用和库存保管费,则其平均利润函数为
(3)
将(1), (2)式代入(3)式,得
(4)
当Q∈(0,+∞)时,有
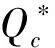
β(p-c-x)Q+(1-β)(Ar+Am)-hQ2-β/[α(2-β)]=0.
(5)

3.2 分散式系统
在分散式系统下,供需双方将进行Stackelberg博弈.销售商对于任何给定的批发价格w,均以自身利润最大化为目标来设置订货量,而生产商作为博弈主导方最终会确定最优批发价格w*,以使自己的平均利润最大.销售商的利润等于其销售收入减去批发成本、订货费用、运输费用和库存保管费,销售商的平均利润为
(6)
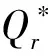
(7)
(8)
生产商需要确定最优的批发价格w以最大化自己的平均利润,由于TPm(w)的最优解一定满足方程dTPm(w)/dw=0.对(8)式求导,得
(9)
而由(7)式知,
(10)
结合(7), (10)式将(9)式化简,得
(11)
令dTPm(w)/dw=0,得
(12)
将(12)式代入(7)式可得
(13)
为判断w*是否为TPm(w)的最大值点,对(11)式求导可得
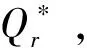
3.3 分摊运费的协调策略
假设生产商向销售商提供如下形式的分摊运输费用的“菜单”:
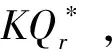
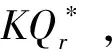
其中,K为销售商订货量是原有最优订货量的倍数,K>1,0 根据假定,要使销售商接受此协调策略,必须保证其利润增量的百分比至少为L.此时生产商的利润等于其销售收入减去生产成本、生产准备费用和分担的运输费用,所以生产商的平均利润函数为 (14) 销售商的平均利润函数为 (15) 因此,生产商要确定K和r的最优值使得自身利润最大的决策可以表示成如下约束优化问题 (16) (17) 其中K>1,0 而生产商只会满足销售商的最低要求,即 (18) 将(15)式代入(18)式可得 (19) 将(19)式代入(14),得 当K>0时,有 (20) 令 显然f(K)是关于K的递减函数,同时由于f(+∞)<0,以及 从而f(K)在(1,+∞)内有唯一的根K*,这即是K的最优值,将K*代入(19)式可得r的最优值r*.又因为在此协调策略下生产商的利润也必须不受损失,即 可以得到L的最大值L*为 当L∈(0,L*)时,对(19)式作等价变形,有 (21) 结合(21)式以及w-c-x<0,可以推出当L∈(0,L*)时必有0 f(u)=β(p-c-x)uβ-1+(1-β)(Ar+Am)uβ-2-h/α(2-β)=0. 显然df(u)/du<0.又由于 f(0)=+∞>0,f(+∞)=-h/α(2-β)<0, 为说明本模型的求解过程及其现实应用,现给出一个具体算例.供应链系统的相关参数如下: α=40,β=0.3,p=40,c=20,x=12,Am=80,Ar=20,h=0.5,λ=60. 下面分析单位产品的运输费用x对供需双方的影响,见表1所列. 表1 单位产品的运输费用x对最优解的影响 由表1可得出以下结论: (i) 随着x的增加,w*,k*和r*均逐渐减小.这是因为x增大意味着运输费用的提高,生产商为了提高销售商的订购积极性,w*,k*就要随之减小,同时生产商为获取高利润,必然降低分担运输费用的比例r*,故模型是符合实际情况的; (iii) 经过分担运输费用策略的协调后,供需双方的利润都增加了,说明该协调策略是可行的,合理的. 本文在需求率依赖于当前库存水平条件下,研究了由单一销售商和单一生产商组成的两层非一体化供应链的协调问题.与已有需求受库存水平影响下的供应链协调模型不同,本模型考虑产品的运输费用为订货量的函数,产品库存费包含两部分费用,并提出了分担运输费用的协调策略.研究结果表明该协调策略能使得供应链达到完美协调.模型可进一步研究易腐品的协调、多销售商、多层供应链等情形. [参 考 文 献] [1] Levin P I, McLaughlin C P, Lamon R P, et al. Productions/Operations Management: Contemporary Policy for Managing Operating Systems [M]. New York: McGraw-Hill, 1972: 373. [2] Gupta R, Vrat P. Inventory model for stock-dependent consumption rate [J]. Opsearch, 1986, 23(1): 19-24. [3] Sarkar B, Sarkar S. An improved inventory model with partial backlogging, time varying deterioration and stock-dependent demand[J]. Economic Modelling, 2013,30(1): 924-932. [4] Pando V, García-Laguna J, San-José L A. Optimal policy for profit maximizing in an EOQ model under non-linear holding cost and stock-dependent demand rate [J]. International Journal of Systems Science, 2012, 43(11): 2160-2171. [5] Yang Chih Te. An inventory model with both stock-dependent demand rate and stock-dependent holding cost rate[J].International Journal of Production Economics,2014,155(1):214-221. [6] 田立平,孙群. 需求受库存水平影响的短生命周期物品延迟订货的库存管理[J].数学的实践与认识,2014,44(5): 128-133. [7] 段永瑞,杨瑾,霍佳震. 需求依赖于展示区库存水平的易腐品订购和转运策略[J].运筹与管理,2014,23(4):51-57. [8] 闵杰,周永务. 库存水平影响需求变化的供应链协调[J].复旦学报:自然科学版,2007,46(4): 523-533. [9] 贾涛,徐渝. 需求依赖于库存量的供应链商业信用期问题研究[J].运筹与管理,2009,18(3):8-14. [10] Zhong G Y, Zhou Y W, Improving the supply chain’s performance through trade credit under inventory-dependent demand and limited storage capacity[J]. International Journal of Production Economics,2013,143(2):364-370. [11] 李琳,周永务. 弹性需求下带有分摊运费的供应链协调策略[J].计算机集成制造系统,2007,13(1): 171-177.
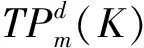

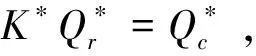
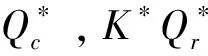

4 算例和灵敏性分析


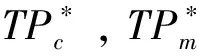
5 结束语
