非标准形式的指派模型在资源分配问题中的应用

马锦娟， 姚晓鹏， 郑 挺

(浙江工商大学 统计与数学学院，杭州 310018)

1 引 言

1951年美国学者Richard.Bellman提出了动态规划,用以解决各类多阶段决策问题[1]. 其基本原理是Bellman的最优性定理并由此导出的最优性原理[2]. 其求解步骤:首先建立问题的动态规划模型(划分阶段,选择问题的状态变量和决策变量,列出状态转移方程,描述问题的指标体系,列出动态规划方程).其次,递推计算(按所列出的动态规划方程分阶段逐一计算).最后,以递推计算结果为基础,以状态转移方程为纽带,按与递推计算相反方向寻找最优策略[3].对一类资源平行分配问题,文献[4]给出一种匈牙利方法.由资源平行分配的特点,我们根据人数少于任务数的指派模型(非标准指派模型[3])给出一种求解的方法.

2 人数少于任务数的指派模型

设有n人,m项工作(n≤m),每人可做多项工作,每项工作只被一人做.效率(或损失)矩阵为

问如何安排可使总的效率达到最大(或损失最小).

设

则该问题的线性规划模型:

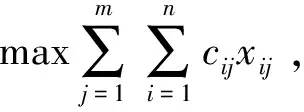
3 资源平行分配问题的“人数少于任务数的指派模型”求解方法

为了叙述方便,首先给出

定义[5]设n,n1,n2,…,nk均为正整数,称n=n1+n2+…+nk为整数n的一个k分部的分拆.若该分拆与n1,n2,…,nk的顺序有关,则称为有序分拆;否则称为无序分拆.另外,若对ni(i=1,2,…,k)有限制,则称为有限制分拆,否则称为无限制分拆.

在资源平行分配中,正整数n的分拆中允许ni=0(i=1,2,…,k).

对于资源总量为n,被分配的部门数量为k及效率(或收益或损失等)矩阵为A=(aij)(aij表示第j部门分配到第i种资源的数量)的分配问题,下面我们总是假设需要资源的部门称为指派问题中的“任务”(有几个部门即表示有几项“任务”),资源的一种分配称为指派问题中的“人”(有几种资源的分配即表示有几个“人”).

指定n的k分部有限制无序分拆n=y1+y2+…+yk,对应一个效率矩阵U(y1y2…yk),其第i行为A中的第yi行.若yi=yj,此时出现第i行与第j行相同,则只写一行,相同的行不重复写.此时还需要特别强调的是,由yi(资源的一种分配)这个“人”与yj这个“人”相同,所以,yi这个“人”需要完成两项“任务”.

下面是所介绍的方法的具体步骤:

(a) 写出分配问题的效率矩阵A和资源总量n的所有k(个部门)分部有限制无序分拆;

(b) 对每一个分拆y1,y2,…,yk,写出对应的效率(或收益或损失)矩阵U(y1,y2,…yk);

(c) 根据1的内容,写出U(y1,y2,…yk)对应的线性规划模型(若有ni个yi相同,则表示yi这个“人”需要完成ni项任务)并求解;

(d) 所有解中的最大者(或最小者)即为所求.

4 应用举例

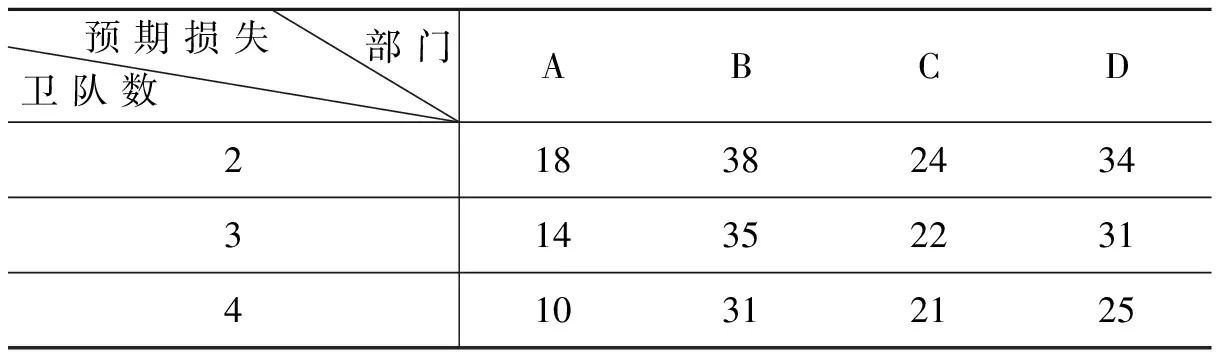
某警卫部门有12支卫队负责A, B, C, D四个要害部门,每个部门需要2-4支卫队巡逻.派出的卫队数不同,则各部门预期在一段时间内可能造成的损失有差别,如下表所示:

预 期 损 失部 门卫 队 数A BCD2183824 34314352231410312125

问应往各部门派多少支卫队巡逻,可使总的预期损失最小？

解此问题中,资源总量为12,部门有四个: A, B, C, D,对应于指派问题中有四项“任务”;资源分配有三种:2，3，4,对应于指派问题中有三个“人”.四项任务被三人完成.

(a) 损失矩阵为

令变量yi(i=1,2,3,4)为派往第i部门的卫队数.于是得整数12的所有4部有限制的无序分拆为

12=y1+y2+y3+y4, 2≤yi≤4, 1≤i≤4.

共有三种不同分拆:

12=4+4+2+2 12=4+3+3+2 12=3+3+3+3.

(b) 对第一种分拆12=4+4+2+2表示向四个部门中的两个部门各派4支卫队,向另外两个部门各派2支卫队.下面具体的求出向哪两个部门派4支卫队, 向哪两个部门派2支卫队.

将四个部门A, B, C, D称为四项“任务”;由于该分拆(y1=y2=4,y3=y4=2)中只有2,4两个不同的数(是资源的两种不同分配),由于2,4在排列中各出现两次,此时损失矩阵U(2244)(由A中2和4所在的行组成,即由A中第一和第三行组成,相同的行不重复写)为

对第二种分拆12=4+3+3+2表示向四个部门中的两个部门各派4支和2支卫队,向另外两个部门各派3支卫队,下面具体的求出向哪两个部门分别派4支和2支卫队,向哪两个部门各派3支卫队.

四项“任务” A, B, C, D被2,3,4这三个“人”来做.由于该分拆中只有2,3,4三个不同的数,此时损失矩阵为(由矩阵A中2,3,4所在的行组成,相同的行不重复写)

对第三种分拆12=3+3+3+3,表示向四个部门各派3支卫队.

四项“任务” A, B, C, D被3这一个“人”来完成.由于该分拆中只有3这一个数,此时损失矩阵为

U(3333)=(14 35 22 31).

(c) 由1得U(2244)对应的线性规划模型(由于2,4在排列中各出现两次,所以2这个“人”和4这个“人” 对这四项工作各做两项):

min18x11+38x12+24x13+34x14+10x21+31x22+21x23+25x24，

由文献[6]中Matlab计算得

x12=x13=x21=x24=1, 其它xij=0.

即向A部门派4支卫队, 向B部门派2支卫队, 向C部门派2支卫队, 向D部门派4支卫队,最小损失为97.

继续由1得U(2334)对应的线性规划模型(注意到该分拆中,2出现一次,3出现两次,4出现一次,这说明,2这个“人”只做一项工作,3这个“人”做两项工作,4这个“人”做一项工作):

min18x11+38x12+24x13+34x14+14x21+35x22+22x23+31x24+10x31+31x32+21x33+25x34,

由Matlab计算得

x13=x21=x22=x34=1, 其它xij=0.

即向A部门派3支卫队, 向B部门派3支卫队, 向C部门派2支卫队, 向D部门派4支卫队,最小损失为98.

由1得U(3333)对应的线性规划模型(注意到该分拆中,3出现四次,所以,3这个“人”要完成4项“任务”):

min14x11+35x12+22x13+31x14,

此时最小损失显然为14+35+22+31=102.

(d) 由min{97,98,102}=97知,应该选择方案:

向A部门派4支卫队,向B部门派2支卫队, 向C部门派2支卫队,向D部门派4支卫队.最小损失为97.

5 结束语

文献[4]中,对n的任一个k分部划分(分拆),用FORTRAN77程序必须求解一个有k2个决策变量且有2k个约束条件的0-1规划问题.当某个分拆中有相同的数时,本文模型中有着决策变量少且约束条件少的优点.如3的例中,分拆2244对应的0-1规划模型中,决策变量只需8个,约束条件6个;若用[4]中的方法,决策变量需要16个,约束条件要8个.

[参 考 文 献]

[1] 杨超，熊伟，白亚根. 运筹学[M]. 北京:科学出版社,2004:232-234.

[2] 陈华友. 运筹学[M]. 合肥:中国科学技术大学出版社,2008:191-195.

[3] 吴祈宗. 运筹学[M]. 北京:北京理工大学出版社,2011:157-158,168-169.

[4] 赵茂先，万贤美，黄珍. 匈牙利方法在资源分配问题中的应用[J]. 山东科技大学学报(自然科学版),2001(2):18-20.

[5] 卢开澄，卢华明. 组合数学[M]. 北京:清华大学出版社,2002:80-85.

[6] 张伯生，范君晖，田书格. 运筹学[M]. 北京:科学出版社, 2008:158-161.