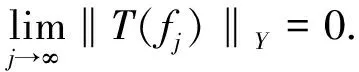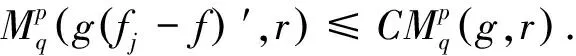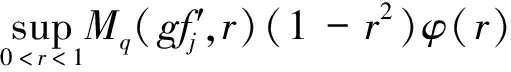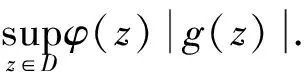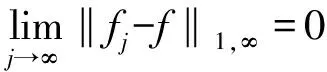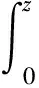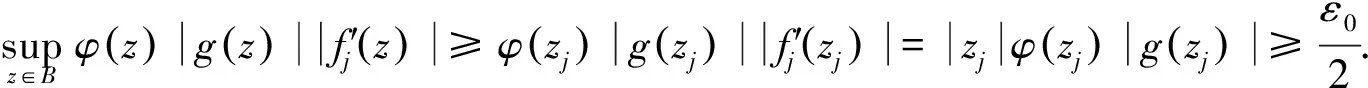若干全纯函数空间上的一类积分算子
2014-09-17吕小芬
曹 燕, 吕小芬
(湖州师范学院 数学系, 浙江 湖州 313000)
1 引 言
设D是C中的单位圆盘,D上全纯函数的全体记作H(D). 定义空间
设φ是[0,1)上的正规权函数. 给定φ和0 定义混合模空间Hp,q,φ是指H(D)中满足‖f‖p,q,φ<∞的函数f的全体. 这里 对任意f∈H(D), 胡[1]指出 (1.1) 定理1设φ是正规权, 0 (i)Lg∶H1,∞→Hp,q,φ是有界的; (ii)Lg∶H1,∞→Hp,q,φ是紧的; (iii)g∈Hp,q,(1-r2)φ. 进一步地, ‖Lg‖H1,∞→Hp,q,φ≅‖g‖p,q,(1-r2)φ 证(ii)⟹ (i) 显然成立. (i)⟹ (iii). 令f(z)=z,则f∈H1,∞且G(z)-G(0)=Lgf(z)∈Hp,q,φ, 其中G是g的一个原函数. 由(1.1) 知g∈Hp,q,(1-r2)φ, 且 ‖g‖p,q,(1-r2)φ≅‖G(z)-G(0)‖p,q,φ=‖Lgf‖p,q,φ≤C‖Lg‖H1,∞→Hp,q,φ. (2.1) 对f∈H1,∞, 由于Lgf(0)=0, 结合(1.1) ,有 →0 (j→∞). 从而可知,Lg∶H1,∞→Hp,q,φ是紧的. 进一步, 对任一f∈H1,∞, 由(1.1) 可知 结合(2.1) 我们有‖Lg‖H1,∞→Hp,q,φ≅‖g‖p,q,(1-r2)φ. 定理2设φ是正规权,g∈H(D), 则下列条件等价: (i)Lg(H1,∞)⊆Bφ,0; (ii)Lg∶H1,∞→Bφ,0是有界算子; (iii)Lg∶H1,∞→Bφ是紧算子; (iv)Lg∶H1,∞→Bφ,0是紧算子; (v)G∈Bφ,0, 其中G为g的一个原函数. 证(ii)⟹(i)和(iv)⟹(iii)显然成立. (ii)⟹ (v). 类似于定理1, 令f(z)=z, 则G∈Bφ,0且 (2.2) (v)⟹(ii). 对任意f∈H1,∞ (2.3) 因此h(0)=0且对任意z∈D, 当j→∞时, 所以f′(z)g(z)=h′(z). 因此, 综上所述,Lg∶H1,∞→Bφ,0是一个闭算子. 由闭图像定理得,Lg∶H1,∞→Bφ,0有界. 两者矛盾. 所以G∈Bφ,0. 其中C 与ε无关. 从而可知Lg∶H1,∞→Bφ,0是紧算子. [参 考 文 献] [1] Hu Zhangjian. Extended Cesaro operators on mixed norm spaces[J]. Proc. Amer. Math. Soc., 2003, 131: 2171-2179. [ 2 ] Pommerenke Ch. Schlichte funktionen und analytische funktionen von beschrankter mittlerer oszi-lation[J]. Comment Math. Helv., 1977, 52: 591-602. [ 3 ] Aleman A and Siskakis A G. An integral operator onHp[J]. Complex Variables, 1995, 28:149-158. [ 4 ] Aleman A, Siskakis A G.Integration operators on Bergman spaces[J]. Indiana University Math.J., 1997, 46: 337-356. [ 5 ] Aleman A, Cima J. An integral operator onHpand Hardy’s inequality[J]. J. Anal. Math., 2001, 85: 157-176. [ 6 ] 王漱石, 胡璋剑. Bloch 型空间上的广义Cesaro 算子[J]. 数学年刊, A 辑, 2005, 26(5): 613-624. [ 7 ] Li Songxiao, Stevic S. Riemann-Stieltjes operators between different weighted Bergman spaces[J]. Bull. Belg. Math. Soc. Simon Stevin, 2008, 15(4): 677-686. [ 8 ] Li Songxiao, Stevic S, Riemann-Stieltjes operators from H1 space toα-Bloch spaces[J]. Integral Transforms Spec. Funct., 2008, 19: 767-776. [ 9 ] Sharma A K, Sharma S D. Riemann-Stieltjes operators between weighted Bloch and weighted Bergman spaces[J]. Int. J. Contemp. Math. Sci., 2007, 2: 759-772.

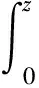
2 主要结论