分析动力学三个问题的研究进展*

梅凤翔 吴惠彬

(1．北京理工大学宇航学院，北京 100081)(2．北京理工大学数学学院，北京 100081)

分析动力学三个问题的研究进展*

梅凤翔1吴惠彬2†

(1．北京理工大学宇航学院，北京 100081)(2．北京理工大学数学学院，北京 100081)

分析力学的发展涉及理论的和应用的诸多方面．本文在分析力学与数学交缘的三个问题上综述分析力学的近代发展．第一是利用Lie群和Lie代数的一些成果来研究分析动力学方程的积分问题．第二是将分析力学的经典和近代积分方法应用于一般微分方程的积分问题．第三是将分析动力学方程在一定条件下化成梯度系统的方程，再用梯度系统的性质来研究力学系统的动力学行为．

分析力学， Lie群， Lie代数， 梯度系统， 动力学方程积分

引言

分析力学从它诞生开始就与数学结下不解之缘．分析力学历史上做出重要贡献的学者，如d’Alembert，Lagrange， Hamilton， Jacobi，Poincaré，Lyapunov等，既是力学家，又是数学家．1982年在意大利都灵由IUTAM－ISIMM联合举办的“分析力学近代发展讨论会”上，会议主席Lichnerowicz在开幕式上说“十九世纪末某些聪明的人去想，我们的物理学知识除了某些细节外已经很完全了，Lagrange，Hamilton，Jacobi，Poincaré，Lyapunov 的工作也引导人们去想再也没有什么本质的东西可以补充到有限自由度系统去了”．“近三十年来，分析力学发生了根本变化．两个因素:一个是大范围微分几何的进步，另一个是数学分析，特别是流形上泛函分析的进步，促进了这种变化”［1］．Arnold指出:“事实上，许多数学方法和概念都在经典力学中得到应用，如微分方程和相流，光滑映射和流形，Lie群和Lie代数，辛几何和各态历经理论．许多现代数学理论产生于力学中的问题，只有后来才达到抽象的公理形式，并且使得它们难以理解”［2］．

几何动力学是分析力学的一个近代发展方向，并已取得重要进展，例如文献［2－15］．文献［16］综述了Birkhoff系统动力学的研究进展，文献［17］研究了非完整系统稳定性的若干进展，文献［18］研究了对称性与守恒量研究进展，文献［19］对非完整力学给出一些评论．本文试图从分析力学与数学的交缘的几个方面叙述分析力学的近代发展．一是Lie群和Lie代数对分析力学的应用;二是微分方程的力学化;三是分析力学与梯度系统．

1 Lie群和Lie代数的应用

1．1 Lie代数的应用

1)基本概念

Lie代数有丰富的内容，这里列出对分析力学最有用的部分．

Lie代数是域F上的代数L，元素 a，b，c满足规律［20］

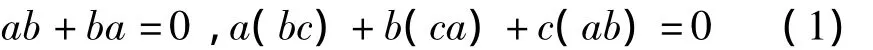
前一式表示积具有反对称性，后一式表示积满足Jacobi恒等式．

Lie容许代数是域F上的代数U，使得附属代数U－是一个Lie代数，由积表征的与U是同一向量空间．

2)动力学方程的代数结构

Lagrange方程和Hamilton方程具有Lie代数结构．特殊非完整系统的方程，包括其相应完整系统的方程具有 Lagrange形式的非完整系统，具有Helmholtz势的 Chaplygin系统［21］，实现非完整系统自由运动的非完整有势系统［22，23］，自治和半自治Birkhoff系统［20，24］等，都具有 Lie 代数结构［25］．

对Hamilton系统，将其表示为逆变形式

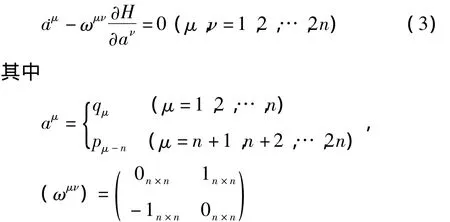
数学工作者侧重研究代数本身，力学和物理学工作者侧重构造代数，并使代数有用．研究某函数A(a)，将按方程(3)求得的对时间的导数A·定义为一个积A◦H:

这个积满足Lie代数公理．对更复杂的力学系统，一般没有Lie代数结构，但有Lie容许代数结构．

3)Poisson方法及其推广

具有Lie代数结构的动力学方程，可直接应用Poisson积分法来求系统的积分;对于具有Lie容许代数结构的动力学方程，可以用推广的Poisson积分法来求系统的积分［25］．

4)问题

对更复杂的动力学系统进一步应用广义Poisson方法求积分仍需深入研究．对于文献［20］中提到的Jordan代数，Jordan容许代数以及交错代数，怎样应用于动力学方程还有待研究．

1．2 Lie群的应用

Lie群是很重要的一类群，有极丰富的内容和广泛的应用．自Noether的工作以来［26］，群的无限小变换用来研究动力学系统的对称性与守恒量取得重要进展．

1)Noether对称性与守恒量

Noether对称性是Hamilton作用量在无限小变换下的一种不变性，由Noether对称性可直接导出Noether守恒量［27－33］．

2)Lie对称性与守恒量

Lie对称性是微分方程在群的无限小变换下的不变性，利用 Lie对称性可求得 Noether守恒量［33－36］，在一定条件下可求得 Hojman 型守恒量［37－40］．

3)形式不变性与守恒量

形式不变性是指微分方程中的动力学函数在无限小变换后仍满足原来方程的一种不变性［41］，利用形式不变性在一定条件下可导出系统的守恒量［42－47］．

4)问题

以上三种对称性以Noether对称性简单、易用，以形式不变性最不易用．用已有对称性继续深入研究更复杂力学系统的守恒量，并发现新的对称性方法是一个重要问题．用计算机寻求近似守恒量也有待开发．

2 微分方程的力学化

微分方程历史的第一个时期是由Newton和Leibniz的工作开始的，……，质点动力学和刚体动力学以及某些几何问题的研究用微积分方法很快就化为一阶或二阶常微分方程中的一类最简单的方程［48］．可见，力学是微分方程的起源之一．同时，力学也促进了微分方程的发展．力学上的难题，往往成为数学上的难题．

分析力学在其发展过程中形成了一整套积分方法，如积分Lagrange方程的Whittaker降阶法［49］和Routh降阶法，积分Hamilton方程的Poisson方法和Hamilton－Jacobi方法，积分不变量方法，场方法［50－52］，势积分方法［53］，Noether 对称性方法，Lie对称性方法，形式不变性方法，Jacobi最终乘子法，Lagrange 对称性方法［54］，共形不变性方法［55－58］等．这些方法对解一般的微分方程也是有效的．为利用分析力学的方法求解微分方程，需将微分方程化成力学系统的方程．

2．1 微分方程的Hamilton化与求解

研究2n个一阶方程

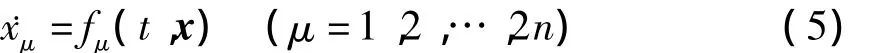
将其两端乘以

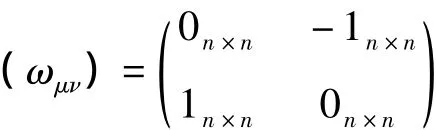
并对ν求和，得

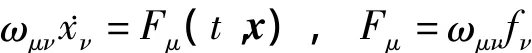
如果函数满足

则可Hamilton化为

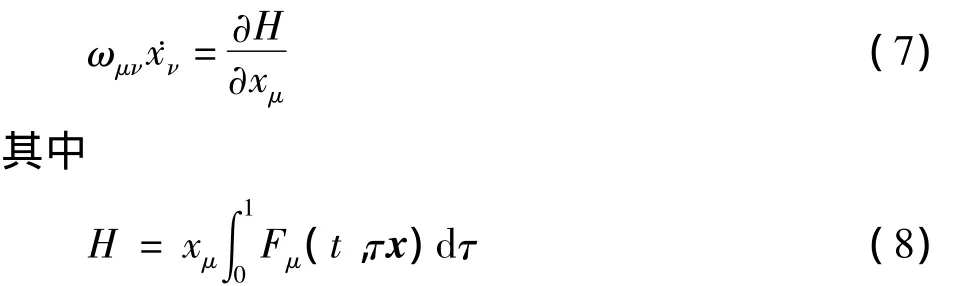
这样，有不少方法可求解方程(7)，如，Hamilton－Jacobi方法［59］，Poisson 方法，场方法，Noether方法等［60］．

2．2 微分方程的部分Hamilton化与求解

如果方程不满足条件(6)，可令

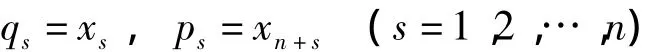
则方程可表示为

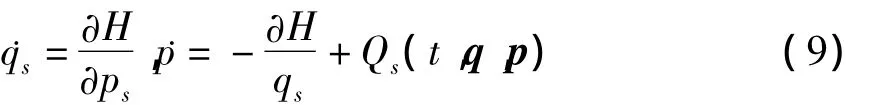
其中Hamilton函数为

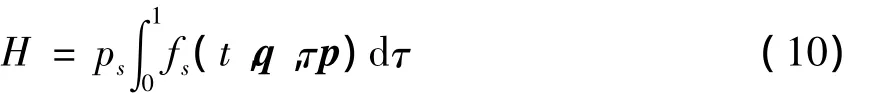
而广义力Qs为

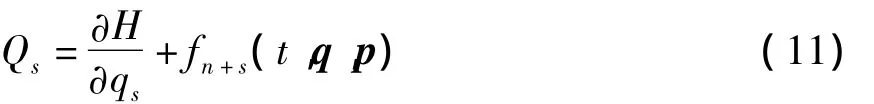
方程(9)是一般微分方程(5)的力学表达，它代表一个一般的完整力学系统．

这样，便可利用一般完整系统的积分方法来求解微分方程(5)，例如，广义Poisson方法，场方法，Noether方法，Lie对称性方法等．

2．3 微分方程的Lagrange化与求解

研究二阶微分方程

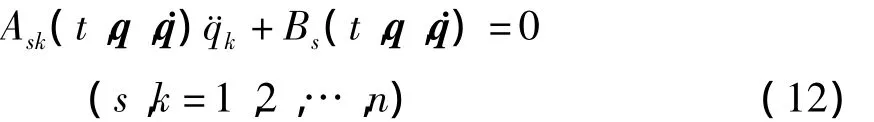
方程(12)在一定条件下可表示为Lagrange方程［61，62］

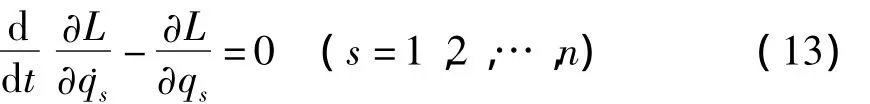
这就是所谓Lagrange力学逆问题．文献［55］称之为Helmholtz系统．

对方程(13)在一定条件下可用降阶法降阶，可将方程(13)表示为 Hamilton方程，进而可用Poisson方法，Hamilton－Jacobi方法等来求解．还可用场方法，Lie方法，Noether方法等求解．

2．4 微分方程的部分Lagrange化与求解

研究二阶微分方程组

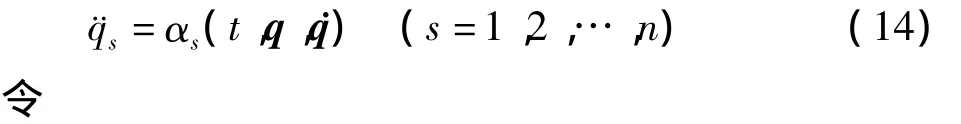
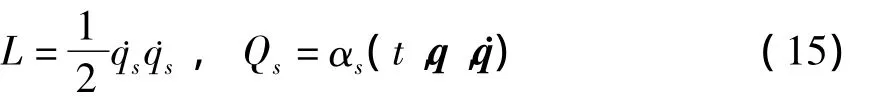
则方程(14)可部分Lagrange化为

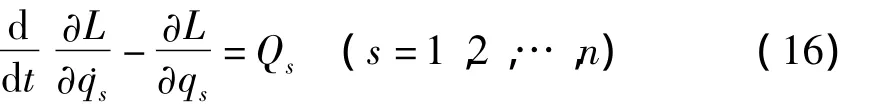
对方程(16)可用广义Poisson方法，Noether方法，Lie方法，形式不变性方法等来求积分．同时，可用Hojman方法，场方法，势积分方法等直接积分方程(16)．

2．5 微分方程的Birkhoff化与求解

微分方程(5)在一定条件下可化为Birkhoff方程

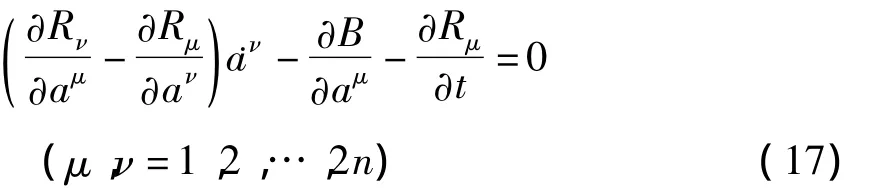
当然，为构造出 Birkhoff函数 B=B(t，a)和Birkhoff函数组 Rμ=Rμ(t，a)还是很难的．

微分方程Birkhoff化后，便可利用Birkhoff系统的一系列积分方法来求解方程(17)，例如，广义Poisson方法，Noether方法，Lie方法，形式不变性方法等．

2．6 微分方程的部分Birkhoff化与求解

文献［63］提出如下方程

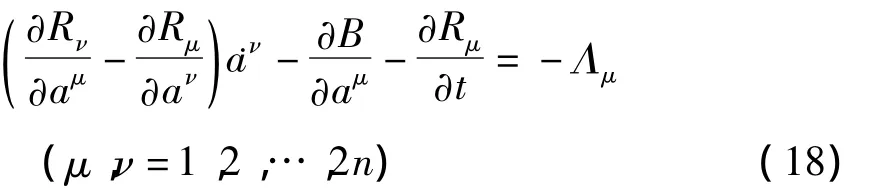
并称之为广义Birkhoff方程，其中 Λμ=Λμ(t，a)为附加项．将方程(5)化成方程(18)称为微分方程的部分Birkhoff化．显然，将方程(5)化成方程(18)要比化成方程(17)容易得多．

如果能够对方程(18)提出并建立积分方法，那么就可解决一般微分方程(5)的积分问题．

关于用分析力学方法求解微分方程的工作见文献［64－66］．

2．7 问题

1)以方程(18)为基础构建广义Birkhoff系统动力学已有少许结果，仍需进一步深入下去．

2)发展分析力学新的积分方法．

3 动力学系统与梯度系统

专著［67］第9章“大范围的非线性技巧”中研究了两类重要系统:一个是梯度系统，另一个是Hamilton系统．梯度系统是微分方程和动力系统中的重要问题，梯度系统有许多好的性质，特别适合用Lyapunov函数来研究．如果动力学方程能够成为梯度系统的方程，那么便可利用梯度系统的特性反过来研究力学系统的动力学行为．

3．1 梯度系统

梯度系统的微分方程有形式

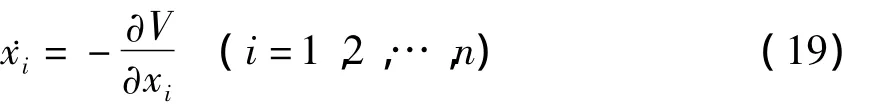
其中 V=V(x1，x2，…，xn)称为势函数．注意到，这个势函数并不是力学系统中的势能．方程(19)可表示为矢量形式

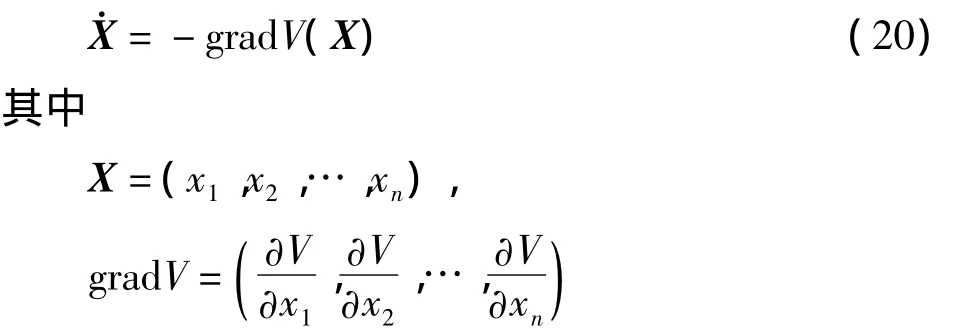
梯度系统有如下重要性质［67］:

1)函数V是系统(20)的一个Lyapunov函数，并且=0，当且仅当X是一个平衡点;

2)设Z是一个梯度流的α极限点或ω极限点，则Z为平衡点;

3)对梯度系统(20)，任一平衡点处的线性化系统都只有实特征根．

如果动力学系统的方程能够成为梯度系统的方程，那么就可利用梯度系统的以上三条性质来研究力学系统的动力学行为，特别是稳定性分析．首先，由梯度系统可找到力学系统的平衡位置;其次，如果能够成为Lyapunov函数，那么就可利用Lyapunov定理研究系统的稳定性，用 Rumyatsev定理［68］研究部分变量稳定性;最后，可直接用第三条性质来判断稳定性．

3．2 斜梯度系统

文献［69］指出，给出一个或几个积分，或Lyapunov函数，则常微分方程可写成线梯度系统．斜梯度系统是线梯度系统的一个重要的特殊情形．如果一个力学系统可以成为斜梯度系统，那么就可利用斜梯度系统的性质来研究力学系统的积分和稳定性．

斜梯度系统的微分方程可表示为

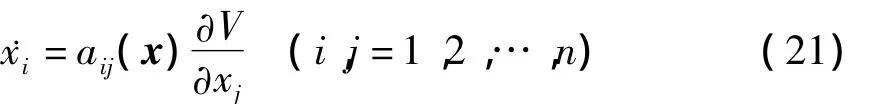
其中aij=－aji．斜梯度系统有如下重要性质［69］:

1)函数V是斜梯度系统(21)的积分;

2)若函数V是一个Lyapunov函数，则零解是稳定的．

以上两条性质可用来研究可化成斜梯度系统的力学系统的积分和稳定性．

3．3 动力学方程的梯度化

1)完整系统

假设系统是定常的，非奇异的，则动力学方程可表示为

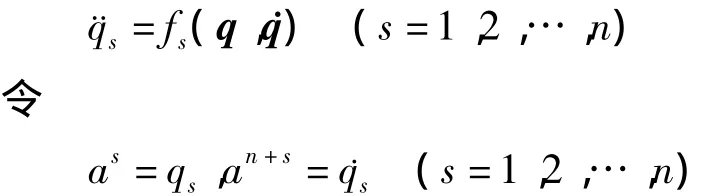
则方程表示为

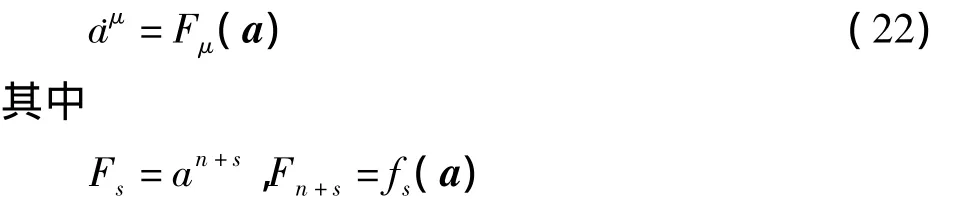
如果满足条件

则方程(21)是一梯度系统．

2)非完整系统

将定常非完整系统化成相应完整系统，可按上述方法讨论相应完整系统的梯度化．

3)Birkhoff系统

自治Birkhoff系统的方程可表示为

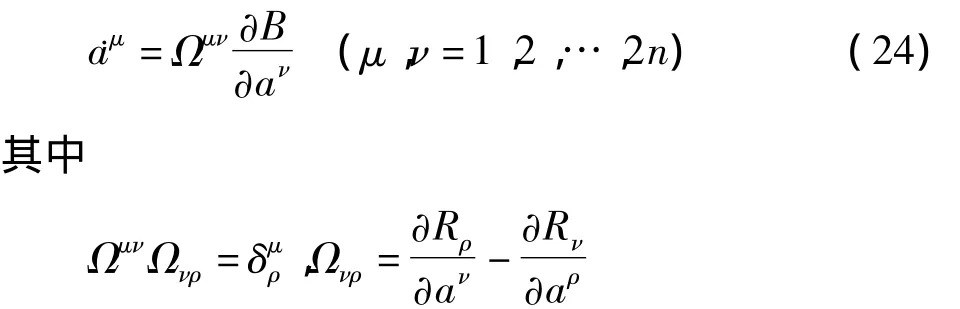
如果满足条件

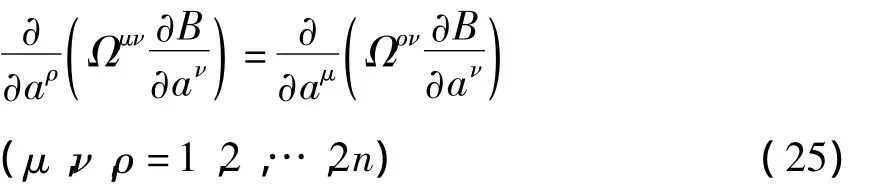
则Birkhoff系统可表示为梯度系统．

3．4 动力学方程的斜梯度化

1)Lagrange系统和Hamilton系统

假设Lagrange系统和Hamilton系统都不包含时间t，则方程可表示为

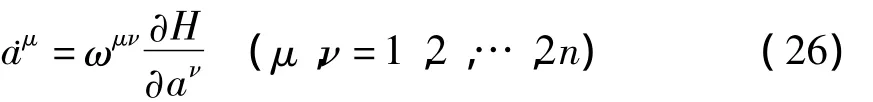
其中

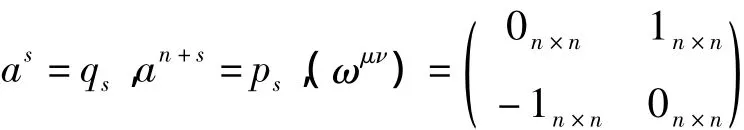
显然，系统(26)是一个斜梯度系统．

2)Birkhoff系统

自治情形的Birkhoff方程有形式(24)，它是一个斜梯度系统．

广义Birkhoff系统的方程有形式［63］

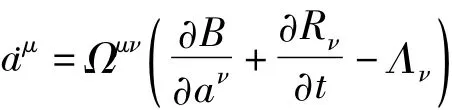
对自治情形，有

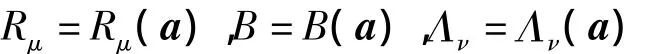
方程(27)可表示为

如果存在函数=(a)，使得

则方程(28)成为

显然，方程(30)是一个斜梯度系统．

3)广义Hamilton系统

广义Hamilton系统的方程为

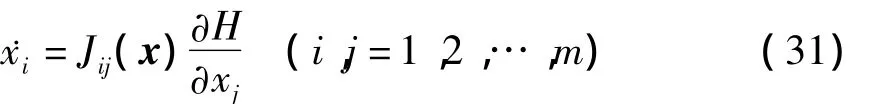
其中Jij=－Jji．显然，广义Hamilton系统(31)是一个斜梯度系统．

3．5 积分和稳定性分析

1)如果梯度系统的势函数可以成为Lyapunov函数，则可利用Lyapunov定理来研究系统的稳定性;

2)如果梯度系统的势函数可以成为Lyapunov函数，则可利用Rumyatsev定理［68］来研究部分变量稳定性;

3)根据梯度系统的第三条性质，对已化成梯度系统的力学系统，可判断不稳定性．

4)斜梯度系统的函数V是一个积分，如果它可以成为Lyapunov函数，则其零解是稳定的．

3．6 问题

1)对非定常系统，能否与怎样化成梯度系统?

2)研究更多更复杂力学系统的梯度化和斜梯度化．

4 结束语

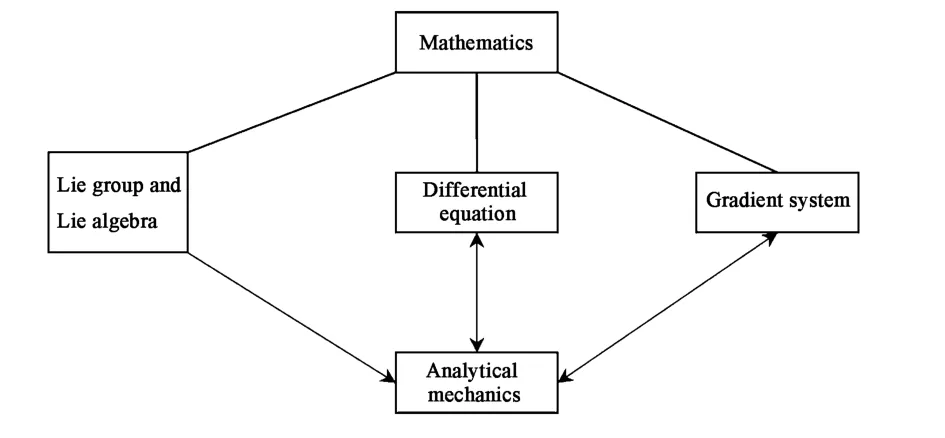
分析力学学科的发展涉及理论的和应用的诸多方面．分析力学200多年的发展历程始终与数学紧密关联着．一方面，数学的进步促进了分析力学的发展．正如IUTAM前主席，工程出身的荷兰著名力学家Koiter指出的，要想使力学进步，一定要用更加抽象更加精密的数学．应用数学的成果来发展分析力学还有待开发．另一方面，分析力学的进步也促进了数学的发展．本文涉及的三个问题，都是分析力学与数学的交缘．第一个问题是将Lie群和Lie代数的一些结果应用于动力学方程的积分．第二个问题是将分析力学的积分方法应用于微分方程的积分．第三个问题是将动力学方程化成梯度系统的方程，再用梯度系统的特性来研究力学系统的行为．最后，用如下框图表示本文的基本思路．

1 Benenti S，Francaviglia M，Lichnerowicz．Proceeding of the IUTAM－ISIMM symposium on modern developments in analytical mechanics．Torino:Acta Acad．Sci．Taurinensis，1983

2 Arnold V I．Mathematical Methods of Classical Mechanics．Berlin:Springer－Verlag，1978

3 Godbillon C．Géometrie differentielle et mécanique analytique．Paris:Hermann，19784 Abraham R，Marsden J E．Foundations of Mechanics．London:The Benjamin/Cummings Publishing Company Inc．，1978

5 Souriau J M．Structure des systèmes dynamiques．Paris:Dunod，1969

6 de León M，Rodrigues P R．Methods of differential geometry in analytical Mechanics．Amsterdam:North－Holland，1989

7 Tulczyjew W M．A generalization of jet theory．Bull．Acad．Polon．Sci．，1978，26:611 ～615

8 Bloch A M，Krishnaprasad P S，Marsden J E，Murray R．Nonholonomic mechanical systems with symmetry．Arch．Rational Mech．Anal．，1996，136:21 ～99

9 Sarlet W，Vandecasteele A，Cantrijn F．Derivations of forms along a map，the framework for time－dependent second－order equations．Differential Geometry and Its Applications，1995，5:171～203

10 刘端，梅凤翔，陈滨．分析力学的数学方法．见:陈滨．现代数学理论与方法在动力学、振动与控制中的应用．北京:科学出版社，1992(Liu D，Mei F X，Chen B．Mathematical methods for analytical mechanics．In:Chen B．Applications of modern mathematical theories and methods in dynamics，vibration and control．Beijing:Science Press，1992(in Chinese))

11 Guo Y X，Luo S K，Shang M et al．Birkhoffian formulations of nonholonomic constrained systems．Reports on Mathematical Physics，2001，47(3):313～322

12 Krupka I，Oliva W M．The non－holonomic mechanics．Journal of Differential Equations，2001，169(1):169 ～189

13 Krupkova O．Recent results in the geometry of constrained systems．Reports on Mathematical Physics，2002，49(2/3):269～278

14 郭永新，罗绍凯，梅凤翔．非完整约束系统几何动力学研究进展:Lagrange理论及其它．力学进展，2004，34(4):477～492(Guo Y X，Luo S K，Mei F X．Progress of geometric dynamics of nonholonomic constrained mechanical systems:Lagrange theory and others．Advances in Mechanics，2004，34(4):477 ～492(in Chinese))

15 吴惠彬，梅凤翔，史荣昌．非完整非保守系统Hamilton原理的几何描述．北京理工大学学报，1993，13(2Ⅱ):260～264(Wu H B，Mei F X，Shi R C．The geometrical representation of Hamilton principle for nonholonomic nonconservative systems．Journal of Beijing Institute of Technology，1993，13(2Ⅱ):260～264(in Chinese))

16 Mei F X．On the Birkhoffian mechanics．International Journal of Non－Linear Mechanics，2001，36(5):817～834

17 朱海平，梅凤翔．非完整系统稳定性的若干进展．力学进展，1998，28(1):17～29(Zhu H P，Mei F X．Developments in the studies of stability of nonholonomic systems．Advances in Mechanics，1998，28(1):17 ～29(in Chinese))

18 梅凤翔．经典约束力学系统对称性与守恒量研究进展．力学进展，2009，39(1):37～43(Mei F X．Advances in the symmetries and conserved quantities of classical constrained systems．Advances in Mechanics，2009，39(1):37～43(in Chinese))

19 Mei F X．Nonholonomic mechanics．ASME，Applied Mechanics Reviws，2000，53(11):283～305

20 Santilli R M．Foundations of theoretical mechanicsⅡ．New York:Springer－Verlag，1983

21 Новосёлов В С．Вариационные Методы в Механике．Ленинград:ЛГУ Изд，1966

22 梅凤翔．非完整系统的自由运动与非完整性的消失．力学学报，1994，26(4):470～476(Mei F X．The free motion of nonholonomic system and disappearance of the nonholonomic property．Acta Mechanica Sinica，1994，26(4):470～476(in Chinese))

23 Зегжда С А， Солтаханов Ш Х， Юшков М П．Уравнения Движения Неголономных Систем и Вариационные Принципы Механики．Новый класс задач управления．Москва:ФИЗМАТЛИТ，2005

24 梅凤翔，史荣昌，张永发，吴惠彬．Birkhoff系统动力学．北京:北京理工大学出版社，1996(Mei F X，Shi R C，Zhang Y F，Wu H B．Dynamics of Birkhoffian system．Beijing:Beijing Institute of Technology Press，1996(in Chinese))

25 梅凤翔．李群和李代数对约束力学系统的应用．北京:科学出版社，1999(Mei F X．Applications of Lie groups and Lie algebras to constrained mechanical systems．Beijing:Science Press，1999(in Chinese))

26 Noether E．Invariante variationsprobleme．Kgl．Ges．Wiss．Nachr．Göttingen．Math．Physik．，1918，2:235 ～257

27 Djukic Dj D，Vujanovic B．Noether’s theory in classical nonconservative mechanics．Acta Mechanica，1975，23:17～27

28 李子平．约束系统的变换性质．物理学报，1981，30(12):1659～1671(Li Z P．The transformation properties of constrained system．Acta Physica Sinica，1981，30(12):1659～1671(in Chinese))

29 李子平．经典和量子约束系统及其对称性质．北京:北京工业大学出版社，1993(Li Z P．Classical and quantal dynamics of constrained systems and their symmetrical properties．Beijing:Beijing University of Technology Press，1993(in Chinese))

30 Liu D．Noether＇s theorem and its inverse of nonholonomic nonconservative dynamical systems．Science China Mathe－matics，1991，34(4):419 ～429

31 Bahar L Y，Kwatny H G．Extension of Noether’s theorem to constrained nonconservative dynamical systems．International Journal of Non－Linear Mechanics，1987，22:125～138

32 赵跃宇，梅凤翔．力学系统的对称性与不变量．北京:科学出版社，1999(Zhao Y Y，Mei F X．Symmetries and invariants of mechanical systems．Beijing:Science Press，1999(in Chinese))

33 陈向炜．Birkhoff系统的全局分析．开封:河南大学出版社，2002(Chen X W．Global analysis of Birkhoff system．Kaifeng:Henan Univ．Press，2002(in Chinese))

34 Lutzky M．Dynamical symmetries and conserved quantities．Journal of Physics A－Mathematical and General，1979，12(7):973～981

35 赵跃宇．非保守力学系统的Lie对称性和守恒量．力学学报，1994，26(3):380～384(Zhao Y Y．Conservative quantities and Lie’s symmetries of nonconservative dynamical systems．Acta Mechanica Sinica，1994，26(3):380～384(in Chinese))

36 Liu R W，Fu J L．Lie symmetries and conserved quantities of nonholonomic systems in phase space．Applied Mathematics and Mechanics，1999，20(6):635 ～640

37 Hojman S A．A new conserved law constructed without using either Lagrangians and Hamiltonians．Journal of Physics A－Mathematical and General，1992，25:L291～L295

38 Luo S K．A new type of Lie symmetrical non－Noether conserved quantity for nonholonomic systems．Chinese Physics，2004，13(12):2182～2186

39 罗绍凯，梅凤翔．非完整系统的非Noether守恒量－Hojman守恒量．物理学报，2004，53(3):666～670(Luo S K，Mei F X．A non－Noether conserved quantity，i．e．Hojman conserved quantity，for nonholonomic mechanical systems．Acta Physica Sinica，2004，53(3):666～670(in Chinese))

40 Zhang Y，Mei F X．Lie symmetries of mechanical systems with unilateral holonomic constraint．Chinese Science Bulletin，2000，45(15):1354～1357

41 Mei F X．Form invariance of Lagrange system．Journal of Beijing Institute of Technology，2000，9(2):120～124

42 Wang S Y，Mei F X．Form invariance and Lie symmetry of equations of non－holonomic system．Chinese Physics，2002，11(1):5～8

43 葛伟宽，张毅．二阶可降阶微分约束系统的形式不变性．物理学报，2003，52(9):2105～2108(Ge W K，Zhang Y．Form invariance for a constrained system with second－order reducible differential constraints．Acta Physica Sinica，2003，52(9):2105～2108(in Chinese))

44 Qiao Y F，Li R J，Ma Y S．Form invariance of Raitzin’s canonical equations of a nonholonomic mechanical system．Chinese Physics，2005，14(1):12～16

45 楼智美．哈密顿Ermakov系统的形式不变性．物理学报，2005，54(5):1969～1971(Lou Z M．Form invariance for Hamiltonian Ermakov systems．Acta Physica Sinica，2005，54(5):1969～1971(in Chinese))

46 陈培胜，方建会．相空间中非完整非保守系统的形式不变性．物理学报，2003，52(5):1044～1047(Chen P S，Fang J H．Form invariance of nonconservative nonholonomic systems in the phase space．Acta Physica Sinica，2003，52(5):1044－1047(in Chinese))

47 Xu X J，Mei F X，Qin M C．Non－Noether conserved quantity constructed by using form invariance for Birkhoffian system．Chinese Physics，2004，13(12):1999 ～2002

48 史捷班诺夫B B．微分方程教程．卜元震译．北京:高等教育出版社，1955(Stepanov V V．A course in differential equations．Translated by Bu Y Z．Beijing:Higher Education Press，1955(in Chinese))

49 Whittaker E T．A traitise on analytical dynamics of particles and rigid bodies．Cambridge:Cambridge University．Press，1904

50 Vujanovic B．A field method and its application to the theory of vibrations．International Journal of Non－Linear Mechanics，1984，19:383～396

51 Mei F X．A field method for solving the equations of motion of nonholonomic systems．Acta Mechanica Sinica，1989，5(3):260～268

52 Kovacic I．On the field method in non－holonomic mechanics．Acta Mechanica Sinica，2005，21(2):192～196

53 Аржаных И С．Поле импульсов．Ташкент:Наука УССР，1965

54 Mei F X，Wu H B．Symmetry of Lagrangians of nonholonomic systems．Physics Letters A，2008，372(13):2141～2147

55 Галиуллин А С，Гафаров Г Г，Малийшка Р П，Хван А М．Аналитичесхая динамика систем гельмгольца，виркгофа，намбу．Москва:УФН，1997

56 Mei F X，Xie J F，Gang T Q．A conformal invariance for generalized Birkhoff equations．Acta Mechanica Sinica，2008，24:583～585

57 He G，Mei F X．Conformal invariance and integration of first－order differential equations．Chinese Physics B，2008，17(8):2764～2766

58 Liu C Mei F X，Guo Y X．Conformal invariance and conserved quantities of non－conservative Lagrange systems by point transformations．Chinese Physics B，2009，18(2):395～399

59 Mei F X，Wu H B，Zhang Y F．Hamilton－Jacobi method for solving ordinary differential equations．Chinese Physics，2006，15(8):1662～1664

60 葛伟宽，黄文华．微分方程的Hamilton化与求解．动力学与控制学报，2006，4(3):201～204(Ge W K，Huang W H．Hamiltonian formularization of differential equations and their method of solution．Journal of Dynamics and Control，2006，4(3):201 ～204(in Chinese))

61 Santilli R M．Foundations of theoretical mechanicsⅠ．New York:Springer－Verlag，1978

62 梅凤翔．分析力学专题．北京:北京工业学院出版社，1988．(Mei F X．Special subjects of analytical mechanics．Beijing:Beijing Institute of Technology Press，1988(in Chinese))

63 Mei F X．The Noether theory of Birkhoffian systems．Sci－ence in China，Series A，1993，36(12):1456～1467

64 Shang M，Guo Y X，Mei F X．A Birkhoff－Noether method of solving differential equations．Chinese Physics，2007，16(2):292～295

65 吴惠彬，张永发，梅凤翔．求解微分方程的Hojman方法．物理学报，2006，55(10):4987～4990(Wu H B，Zhang Y F，Mei F X．Hojman method for solving differential equations．Acta Physica Sinica，2006，55(10):4987～4990(in Chinese))

66 Mei F X，Xie J F，Gang T Q．Analytical mechanics methods for solving Whittaker equations．Chinese Physics，2007，16(10):2845～2847

67 Hirsch M W，Smale S，Devaney R L．Differential equations，dynamical systems，and an introduction to chaos．Singapore:Elsevier，2008

68 Румянцев В В，Озиранер А С．Устойчивость и стабилизация движения по отношению к части переменых．Москва:Наука，1987

69 Mclachlan RI，Quispel GRW，Robidoux N．Geometric integration using discrete gradients．Philosophical Transactions of the Royal Society of London A，1999，357:1021～1045

*The project supported by the National Natural Science Foundation of China(10932002，10972031，11272050)

† Corresponding author E－mail:huibinwu@bit．edu．cn

ADVANCES IN THREE PROBLEMS OF ANALYTICAL DYNAMICS*

Mei Fengxiang1Wu Huibin2†
(1．School of Aerospace Engineering，Beijing Institute of Technology，Beijing100081，China)(2．School of Mathematics，Beijing Institute of Technology，Beijing100081，China)

The development of analytical mechanics involves many aspects of theory and application．This paper summarizes the recent progress of analytical mechanics in three problems on the interdisciplinarity between analytical mechanics and mathematics．The first is to study the integration problem of equations of analytical dynamics by using some results of Lie groups and Lie algebras．The second is to apply the classical and modern integration methods of analytical mechanics to the integration problem of general differential equations．The third is to transform the equations of analytical dynamics into the equations of gradient system under certain conditions and then discuss the dynamical behaviors of the mechanical system by using the properties of gradient system．

analytical mechanics， Lie group， Lie algebra， gradient system， integration of dynamical equations

17 June 2013，

15 July 2013．

10．6052/1672－6553－2013－106

2013－06－17 收到第 1 稿，2013－07－15 收到修改稿．

*国家自然科学基金资助项目(10932002，10972031，11272050)

E－mail:huibinwu@bit．edu．cn