在横向剪切环境下利用 Matlab恢复波前信息
2014-09-12国秀珍陆国会曲延吉
卢 杰,国秀珍,陆国会,曲延吉,韩 力
(1.吉林大学 物理学院,吉林 长春 130021; 2.长春理工大学 光电信息学院,吉林 长春 130012)
1 引 言
常见的干涉方法主要可以分为标准面干涉方法和共路干涉方法. 横向剪切干涉方法是共路干涉方法中一个具有代表性的方法. 横向剪切干涉法的基本原理是以被测波前与其自身的、被剪开的波前之间在重叠范围内相干涉,进而评价被检验波前本身的缺陷. 它的优点在于不需要一个标准波前,缺点是剪切干涉图不能直接判定被测波前形状,需要恢复波前信息,数据处理比较复杂. 因为剪切干涉图直接反映的不是波前信息,其条纹形状表示的是波前相位的平均斜率. 由干涉图得到波前形状的过程则是波前拟合的过程. 迄今为止,有描点法、二维联立解析法、最小二乘法、泽尼克多项式拟合法等,但在许多的测试工作中,相当一部分是利用光学干涉方法来实现完成的.
MathWorks公司开发的程序计算语言Matlab,采用数值计算和图形处理高度集成化的科学计算,已经成为数学计算工具的一个标准. 通过Matlab完成采集、处理、描点全部拟合过程. 它不但降低了描点的工作强度,而且提高了工作效率和精度,为剪切量可变化的实际监测工作提供了快捷有效的途径.
2 横向剪切法实验原理
所谓波前剪切干涉技术,就是通过一定的装置将1个具有空间相干性的波前分裂为2个完全相同或相似的波前,并使这2个波前彼此间存在一定的相对错位,各点是彼此相干的波前在相遇区将产生干涉. 图1为横向剪切干涉仪的实验光路图.
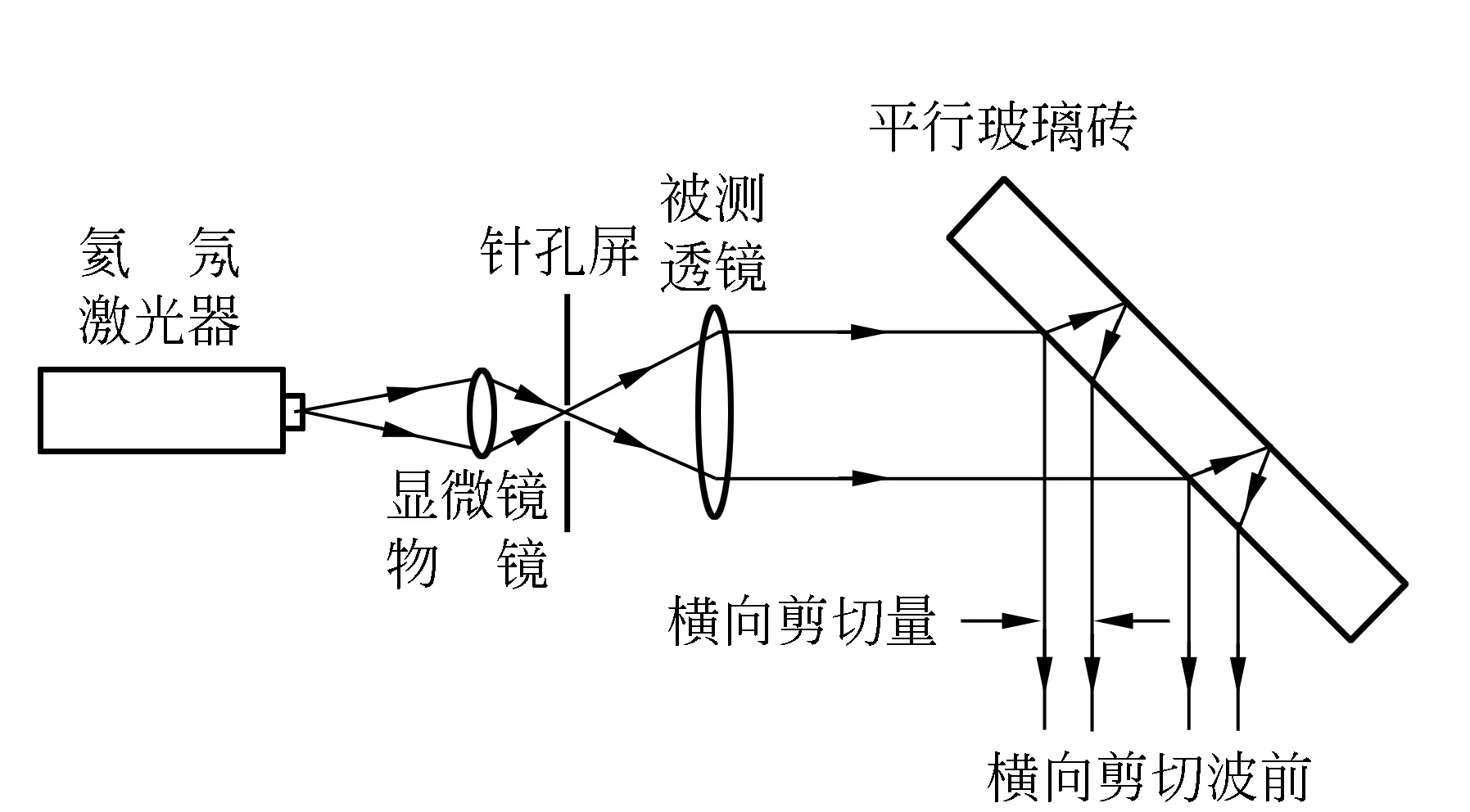
图1 横向剪切干涉仪光路图
因为剪切干涉条纹存在原始波前形状的信息,所以通过干涉条纹的分析和测量,能得到原始波前的波差分布图. 波前剪切是利用分被测波前,再使被分的被测波前重叠,实现干涉,没有参考波前,并且是平面坐标轴x的方向(横向),因此称横向剪切干涉技术. 在光学测量及其他科技生产领域中横向剪切干涉技术被广泛应用.
图2为原始波前和剪切波前及在相遇区的干涉图. 设波前为平面,在波前上任意一点P的坐标为(x,y),W(x,y)表示相对于平面的波差. 当波前在横向剪切量为s时,那么W(x-s,y)就是同一点剪切波前的波差. 所以原始波前和剪切波前在任意点处的光程差ΔW为
ΔW=W(x,y)-W(x-s,y) ,
(1)
光程差ΔW用干涉光的波长表示,N为干涉条纹的级次,λ为波长. 则
ΔW=Nλ,
(2)
在x轴方向,且当剪切量较小时, ΔW可近似表示为
(3)
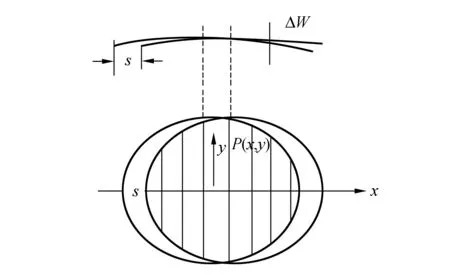
图2 波前形状与干涉条纹
因此,角度计量的光线像差反映了横向剪切干涉信息. 当s→0时,由(3)式表示的光程差更精确. (3)式是恢复波前信息的基本关系式.
3 用横向剪切干涉的图形求原始波前
在通常的情况下,不但要根据干涉图分析波前缺陷,还要定量地分解被测波前的形状,下面根据横向剪切干涉图求原始波前[1].
图3中W(x)为原始波前,W(x-s)为剪切波前,剪切量是s,剪切方向在x轴. 在原始波前W(x)和剪切波前W(x-s)上分别用s为间距取1,2,…,n抽样点,n个抽样点对某参考面的波差分别用W1,W2,…,Wn表示. ΔW(x)表示原始波前和剪切波前光程差,则有
ΔW(x)=W(x)-W(x-s) ,
(4)
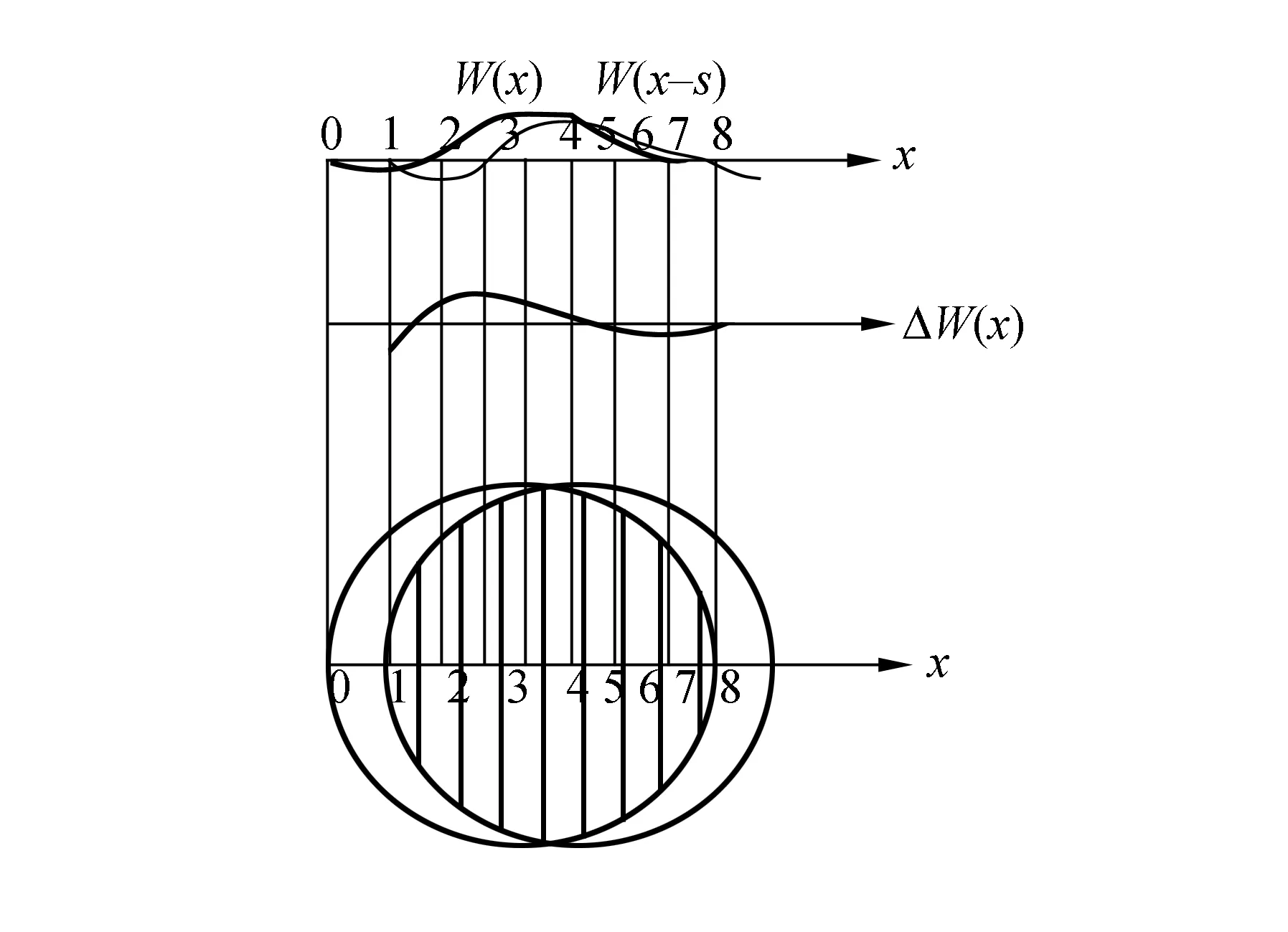
图3 通过干涉图求原始波前解示意图
对图2中的x=s点则有
ΔW(s)=W(s)-W(0) ,
(5)
置W(0)=0则
W(s)=ΔW(s) .
(6)
同样对于x=2s点可得
ΔW(2s)=W(2s)-W(s) ,
(7)
W(2s)=ΔW(2s)+W(s)=ΔW(2s)+ΔW(s) .
(8)
依次类推可以写出
W(ns)= ΔW(s)+ΔW(2s)+… +ΔW(ns)

(9)
通过以上分析可知,在干涉图上测出n个抽样点处的光程差ΔW(ns),全部抽样点求和,求出各抽样点的波差W(ns),利用(3)式可以做出波差曲线.
4 实验装置
实验流程如图4所示,氦氖激光器发出波长632.8 nm,准直系统可检测频谱宽度不低于90 nm,单平板平晶(表面未镀膜)为干涉系统的核心器件,剪切量1.10 mm. 通过CCD摄像机采集图像,然后经过数据处理系统,进行滤噪、细化、数据采集和拟合波前.
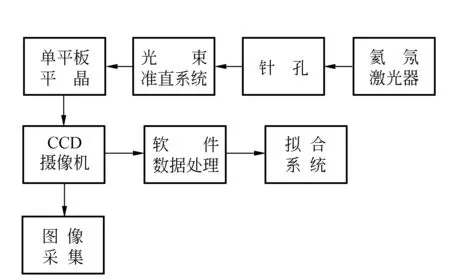
图4 实验流程系统简图
5 拟合波前方法简介
利用计算机描点确定各个参考点干涉级次P,以剪切量整数倍为单位,沿着x轴方向测量,并从x轴起点到各个条纹中心位置的数值及他们的级次记录. 用计算机模拟出x与P的对应关系曲线(如图5). 随意输入P值或x值就可得到相应的x值和P值,精度可达0.01 mm.

图5 x与P的对应关系曲线
通过各参考点的x值记录,确定其参考点的级次P值,用计算机把x和P数据分成分2组或3组.x值可以是偶数组中间两数的平均数,也可是奇数个数据的中间数,而P值取各组的平均数. 这样,通过理想干涉级次与实际干涉级次的偏差值,求出干涉条纹的形变量及波差值,目标确定未知波面情况. 拓展到z方向上积分可以求得完整的未知波面曲线.
6 Matlab拟合波前信息
图6是通过计算机从本实验单平板剪切装置中采集到的比较完整的干涉图样,经过数据处理,滤波、消除噪音并细化后的干涉图样如图7[2-8].

图6 单平板剪切干涉图

图7 滤波、细化后的干涉图样
条纹细化并选择参考面在得到实验条纹下,在Matlab环境下细化,并确立参考面. 用作图解析法拟合未知波面,图8为理想干涉级次积分后构成波面的主视图,理想波前干涉成像后,干涉条纹为等间距直条纹,那么Y=AX+B平面为理想级次积分曲面.

图8 理想干涉级次积分后构成波面的主视图
图9是计算机处理后得到的实际干涉级次与理想干涉级次之差所构成的积分曲面主视图,它在一定程度上反映了待测波前的实际状况.

图9 实际级次与理想级次差的积分曲面主视图
把实际干涉级次与理想干涉级次偏差所构成的积分平面做积分,得到单平板剪切干涉图样实际波前如图10所示.
从实际波面的x-y面等高线投影如图11所示,可以比较完整地体现出实际波面的缺失.
本文在利用解析和二维制图法拟合剪切干涉图的理论基础之上,拓展到三维情况,并用自主调试的单平板剪切干涉系统,利用Matlab进行自动化采样和数据处理过程,并比较完成和准确地拟合出未知波面的实际情况.

图11 实际波前在x-y面上等高线
7 结束语
本实验比较完整地拟合出未知波面,较高精度再现波前的真实情况,从而对光束的情况进行定性判断和定量调整. 虽然由于条件限制不可避免地存在有一定的误差,但是比人为设定的“参考波前”的方法的误差要小很多,而且在实际的光束线检测中,横向剪切干涉恢复波前信息所造成的误差可用多钟方法进行弥补,会使许多因素造成的误差大大降低. 本实验介绍的恢复波前信息的方法是有效的光检测手段,也可用做大专院校近代物理实验的演示仪器.
参考文献:
[1] 许晓军,陆启生,刘泽金,等. 横向剪切干涉的波前重构新方法[J]. 强激光与粒子束,2001,13(5):263.
[2] 惠梅,牛憨笨. 运用泽尼克多项式进行物面波前数据拟合[J]. 光子学报,1999,28(12):1113-1115.
[3] 韦春龙,陈明仪,王之江. 运用泽尼克多项式的相位去包裹算法[J]. 光学学报,1998,18(7):912-917.
[4] 朱中儒,张国平. 数字散斑剪切干涉光学测距[J]. 华中师范大学学报(自然科学版),2001,35(3):287.
[5] 高必烈. 剪切干涉仪的定量处理数学原理及采样处理技巧[J]. 光学仪器,2001,23(3):31.
[6] 聂士忠,王玉泰. 在Matlab环境中使用ISA扩展槽数据采集板进行信号采集和处理的方法[J]. 物理实验,2004,24(5):20.
[7] 袁丹,刘艺,胡宇明. 基于快速傅里叶变换的二维位移测量的改进[J]. 物理实验,2013,33(4):38.
[8] 赵立强, 柯亮. 复色平面光波与复色发散球面光波干涉的光强分布的模拟[J]. 物理实验,2013,33(7):46.
