用“俯视图法”求正方体个数
2011-02-01453007河南师范大学附属中学刘晨曦付帅
453007 河南师范大学附属中学 刘晨曦 付帅
用“俯视图法”求正方体个数
453007 河南师范大学附属中学 刘晨曦 付帅
利用相同小正方体搭成的几何体的三视图,确定或求最多(少)小正方体个数问题,是近几年中考考查三视图的热点之一.此类试题不仅考查了学生掌握三视图的程度,同时也考查了学生的空间想象能力.如何快捷地求出此类问题的正确答案,本文介绍一种“俯视图法”,与同行商榷.
1 “俯视图法”的依据
1.1 位置关系
俯视图在主视图的正下方,左视图在主视图的正右方.
1.2 大小关系
主视图与俯视图长对正,主视图与左视图高平齐,左视图与俯视图宽相等.这里的长、宽、高分别对应三视图所示物体的左右之间、前后之间、上下之间的长度.
2 “俯视图法”的步骤
第一步:画出俯视图;
第二步:标出俯视图中每个正方形中所代表的正方体个数.方法是:主视图与俯视图遵循“列对列”,即主视图中每列正方形总的个数写在俯视图中对应的列中每个正方形中,例如主视图的第1列上有3个正方形,则在俯视图的第1列上每个正方形中标上3(表示在此位置有3个正方体),以此类推;左视图与俯视图遵循“列对行”,即左视图中每列正方形总的个数写在俯视图中对应的行中每个正方形上,例如左视图的第1列上有3个正方形,则在俯视图的第1行上每个正方形中标上3(表示在此位置有3个正方体),以此类推;
第三步:确定正方体的个数,即由第二步可得俯视图中每个正方形中有两个数字,取较小(若数字相同不变)的数字相加,所得的和即为正方体的个数.
3 “俯视图法”的应用
3.1 确定小正方体个数
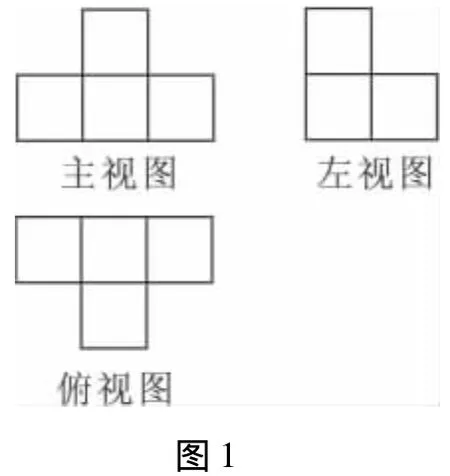
例1 (2010年威海)图1是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是
A.5 B.6 C.7 D.8
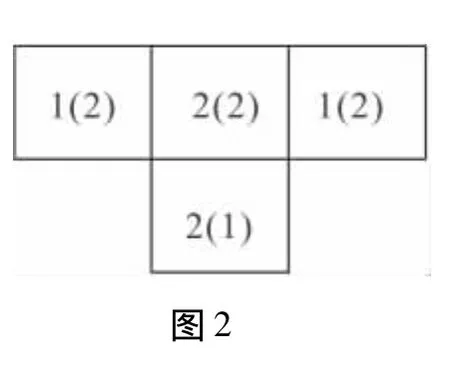
解析 由主视图可知在俯视图第1、3列每个正方形内填1,第2列每个正方形内填2;又由左视图可知,在俯视图的第1行中每个正方形内都填2,第2行填1,如图2所示,重叠交叉处应取两次所填数字中较小的,则1+2+1+1=5,即几何体的小正方体的个数是5,故选A.
3.2 求最值
(1)给出主视图、左视图求最大值
例2 (2010年河南)如图3是由大小相同的小正方体组成的简单几何体的主视图和左视图,那么组成这个几何体的小正方体的个数最多为 .

图3
解析 主视图有2列,左视图有3列,可知几何体的俯视图最多为2×3的长方形(如图4),由主视图可知在俯视图第1列每个正方形内填2,第2列每个正方形内填1;又由左视图可知,在俯视图的1行中每个正方形内都填2,第2,3中行每个正方形内都填1,如图4所示,重叠交叉处应取两次所填数字中较小的,把较小的数字相加得7,所以总体上最多由7个正方体组成.故填7.
(2)给出主视图、俯视图求最小值

图4
例3 (2010年深圳)如图5,是一个由若干个相同的小正方体组成的几何体的主视图和俯视图,则能组成这个几何体的小正方体的个数最少是 个.

图5
解析 主视图的第1列有3个正方形,在俯视图第1列每个正方形内都应填3,但题中要求的是最少的正方体个数,于是在该列中至少有一个正方形内填3,其余填1,同理,在俯视图中的第3列中至少有一个正方形内填2,其余填1,第2列中正方形内只能填1,如图6所示,所以能组成这个几何体的小正方体的个数最少是9个,故填9.

3.3 求可能值
例4 如图7,组成这个几何体的小正方体的块数为n,则n的所有可能值为————.

图7

图8

图9
解析 主视图的第1列有1个正方形,在俯视图第1列的正方形内填1,主视图的第2列有2个正方形,在俯视图第2列的每个正方形内填2,主视图的第3列有3个正方形,在俯视图第3列的每个正方形内填3,如图8所示,于是这样得到的是小正方体块数最多的情况,此时11块;保持俯视图中第1列的个数不变,在俯视图中的第2,3列中分别至少有一个正方形内填2和3,其余填1,如图9所示,这样得到的是小正方体块数最少的情况,此时8块,所以8≤n≤11,因为 n为整数,故 n=8,9,10和11.
20110325)
