一种快速模拟振荡叶栅非定常流的数值方法

施永强，杨青真，黄秀全，郭 霄

（西北工业大学动力与能源学院，陕西西安 710072）

一种快速模拟振荡叶栅非定常流的数值方法

施永强，杨青真，黄秀全，郭 霄

（西北工业大学动力与能源学院，陕西西安 710072）

为了提高叶轮机内周期性非定常流数值计算效率，发展了一种计算振荡叶栅非线性非定常流的谐波平衡方法，将周期性非定常流动参数采用傅里叶级数表示，从而将传统的定常流动数值计算方法应用于非定常流问题求解中，大大提高了非定常流计算效率。计算结果表明，发展的谐波平衡方法与线性方法、非线性时域法计算结果吻合较好，且其计算效率比时域法高1个数量级。另外，系统研究了谐波阶次对计算效率与计算精度的影响，认为在气流未出现严重分离时，应采用低阶谐波平衡方法，以减少计算耗时。此外，从压气机振荡叶栅非定常流场计算结果可以看出，叶片吸力面诱导涡的生成频率与振荡频率并不一致，涡生成频率要高于振荡频率。

振荡叶栅；谐波平衡方法；非定常流；双时间法；形状修正法

0 引 言

叶轮机内流场具有高度复杂的非定常性。传统的二维轴对称气动设计理论和全三维定常流场计算方法，都无法反映这一真实的流动特性。用这种定常流体系处理具有强烈非定常特征的叶轮机设计问题时，从一般意义上讲，会导致对非定常流“潜力”的某种忽略而使性能有所损失。叶轮机械中的叶片是弹性体，在气动力、结构等因素影响下，会发生振动。强的振动现象会导致叶片在短时间内断裂，造成严重的后果。为了深入研究叶栅非定常流动，探索叶轮机械强迫振动、颤振的发作机理，就必须对振荡叶栅非定常流场以及叶片所产生的周期性非定常气动力的性质给予准确、高效地模拟与预测。

目前，利用计算流体力学方法对振荡叶栅非定常绕流及叶片所受气动力进行数值模拟，进而分析振荡叶片与流场间的相互作用，已成为研究叶片强迫振动与颤振的重要手段。在振荡叶栅非定常流动数值模拟研究方面，传统的分析方法是时间推进方法。但是，由于时间推进方法计算过程中要采用统一的时间步长推进，因此计算工作量特别大，计算相当耗时。1991年，Jameson提出了双时间方法［1］，提高了非定常流动计算效率。与时间推进方法相比，这种方法计算速度是传统方法的7～9倍［2］，因此被广泛应用于非定常流动数值模拟。

虽然双时间方法能够加速非定常流动数值计算，提高计算效率，但对于复杂的叶轮机械非定常流动来说，其计算工作量还是相当巨大的。为此，国外学者在这方面做了大量的研究工作，发展了高效的频域计算方法求解非定常流动。Verdon［3］，Whitehead［4］和Hall［5］等人分别提出了模拟二维叶栅非定常流动的时间线化方法；Hall和Lorence发展了三维线化非定常流动计算方法［6］；2005年，Ekici和Hall采用时间线化方法分析了多级叶轮机械颤振问题［7］。时间线化方法在求解叶轮机械非定常流动问题时，仅需要模拟单个通道的流动状况，且其计算时间与定常流动计算时间相当，因此，被广泛应用于叶轮机非定常流动数值模拟中。然而，时间线化方法也存在着不可忽视的缺点——忽略了非定常流动的非线性现象。为此，Hall提出了谐波平衡方法用于模拟叶栅中非线性非定常流动，计算结果表明这种方法计算非定常流比传统的时域方法快1到2个数量级，而且这种方法可以精确地计算非线性很强的非定常流场［8］。此后，Hall将这种方法应用于各种叶轮机非定常流动问题分析当中，取 得了 一 系列 的 成果［9-12］。

本文分别采用谐波平衡方法和双时间方法求解二维Navier-Stokes方程，对振荡叶栅非定常粘性流动进行了数值模拟，对比分析了谐波平衡方法的计算效率与计算精度。同时，将伪边界形状修正方法引入非定常流动计算程序中，大大缩短了振荡叶栅存在相差时的非定常流计算时间。此外，采用谐波平衡方法分析了某压气机叶栅在非定常气动力作用下的气动弹性稳定性，探讨了振荡叶栅相位差对气弹稳定性的影响。

1 计算方法

1.1 控制方程

在直角坐标系下，对于运动网格，积分形式的二维雷诺时均Navier-Stokes方程可写为：

写成半离散化的格式

其中U=［ρ，ρu，ρv，e］T，E、F是无粘通量，Eν、Fν是粘性通量，u和v 分别是x 和y 方向的速度分量，e=分别为 两个方向 的网格移动速度。

1.2 谐波平衡方法

谐波平衡方法最早由Hall［8］提出，其主要思想是将周期性函数采用傅里叶级数表示。振荡叶栅中的流体流动是周期性函数，因此流场中的守恒变量可以展开成傅里叶级数的形式：

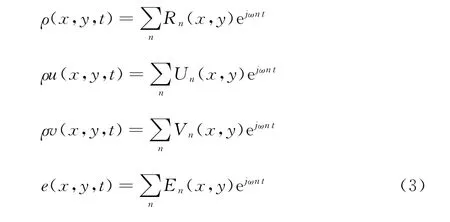
其中，Rn（x，y）、Un（x，y）、Vn（x，y）和En（x，y）分别是四个守恒变量的n阶傅里叶系数，ω是周期函数的角频率。

为了更清楚地表示式（3）中的变量，我们以U 表示任意变量，并以三角形式表示傅里叶级数，在忽略N 以上的高阶项之后，即有

其中，A0、An和Bn是变量U 的傅里叶系数。

在一个周期内，选取2N+1个时间点，式（4）可写成矩阵形式

其中U*表示在2N+1个时间点上的守恒变量向量，E表示离散傅里叶逆变换算子，~U 表示守恒变量的傅里叶系数向量。由此式（5）可写为

相反，守恒变量的傅立叶系数向量可通过傅立叶变换得到

其中，E-1表示离散傅立叶变换矩阵。

由此，通过时域控制方程式（1）可得频域控制方程

这里，E*、F*分别为x、y方向的通量。

式（8）表示了2N+1个控制方程组，不同时刻的控制方程通过时间导数项耦合。时间导数项可表示为：

其中D为频域算子。

由此，把时间导数项作为源项可得谐波平衡控制方程：

1.3 数值计算方法

方程（10）为一个周期内2N+1个时间点上的控制方程，其方程个数为4×（2N+1）。为了求解谐波平衡方程，可以引入一个伪时间项，这样方程就可以采用传统的时间推进方法进行迭代求解。由此可得

方程（11）采用四步Runge-Kutta法在伪时间上推进，并加入二阶和四阶人工黏性系数。采用当地时间步长法、双重网格技术和隐式残差光顺方法加速计算收敛。

1.4 边界条件

边界条件包括进口边界条件，出口边界条件，壁面边界条件和振荡叶栅非定常流动中的相差周期边界条件。上游边界给出总温、总压、气流角，当来流为超声速时，用超声叶栅唯一迎角原理，根据来流马赫数确定进口气流角。即指定进口马赫数来代替指定进口气流角。下游边界给定出口反压，在轴向分速度为亚声速时，出口压力为反压，其他参数外插得到；如果轴向分速为超声速，气动参数外插得到。物面边界条件：采用无滑移条件，对于振荡叶栅，物面边界条件即为u=umg，v=vmg。相差周期边界采用伪 边界形状修正法［13］对周期边界进行处理，从而使得 在相邻叶片存在相位差时，也能采用单通道进行计算。

2 数值计算及结果分析

本文应用谐波平衡方法分别对 NACA0012叶栅、平板叶栅和某压气机典型截面叶栅非定常流场进行了数值模拟。其中，NACA0012叶栅和压气机叶栅做纯扭转振动，平板叶栅做纯弯曲振动。

2.1 NACA0012叶栅

由 NACA0012翼型组成的叶栅，其计算条件如下：进口马赫数M1=0.593，雷诺数Re=3.21×106，进口气流角αm=0°，栅距／弦长=1.0。叶栅作扭转振动，扭转幅度α=2°，振动中心为叶片前缘，相邻叶片振动相位差σ=0°，折合频率k=ωc／（2u∞）=0.2，式中ω为振动角速度，c为叶片弦长，u∞为上游远场边界速度。

分别采用二阶谐波平衡方法和双时间法数值模拟振荡叶栅非定常流动，其计算结果如图1～图3所示。其中一阶非定常压力系数定义为：

式中，p1为压力的一阶谐波分量，ρ∞、u∞分别为上游远场气体密度和速度，Am为扭转振动幅度。

图1 NACA0012翼型上表面一阶非定常压力系数Fig.1 Unsteady pressure coefficient distribution on upper surface of airfoil NACA0012

图2 NACA0012翼型升力系数随时间变化曲线Fig.2 Lift coefficient variation of airfoil NACA0012 in a period

图3 NACA0012翼型升力系数随扭转角度变化曲线Fig.3 Lift coefficient variation of airfoil NACA0012 with the torsion angle

由图1可以看出，谐波平衡方法的计算结果与双时间方法计算结果几乎完全一致。另外与参考文献［14］的计算结果吻合程度也较好，仅在前缘处略有不同。图2为一个周期内翼型升力系数的变化曲线。图中也分别展示了谐波平衡方法、双时间方法以及参考文献［14］的线性方法计算结果。其中双时间方法是截取了已经计算稳定的最后一个周期的计算结果。由图可以看出，谐波平衡方法和双时间方法的升力系数变化也几乎完全一致，其升力系数的波动范围和相位都相互吻合。与参考文献［14］相比，谐波平衡方法升力系数峰值为0.081，双时间方法为0.0805，文献［14］中为0.0763，稍有不同，但其相位一致。图3为升力系数随扭转角度的变化规律，其谐波平衡方法和双时间方法的计算结果也非常吻合。

2.2 平板叶栅

为了验证叶片间存在相差时的计算结果，本文以参考文献［15］的平板叶栅为研究对象，验证本文的计算方法。平板叶栅的弦长c=0.076m，栅距／弦长= 1.3，进口马赫数M1=0.65，进口气流角αm=0°，迎角i=0°。叶栅做弯曲振动，即垂直于弦线方向做平移振动，其弯曲振动幅度为Ba=1%c，振动频率f=250Hz（折合平率k=0.57），相邻叶片振动相位差σ=90°。

图4 平板叶栅非定常压差系数Fig.4 Unsteady pressure jump coefficient distribution for a flat plate cascade

本文采用形状修正方法处理周期相差边界，因此计算采用了一个通道。计算采用二阶谐波平衡方法，每个周期设置五个时间层。图4为计算所得的平板叶栅表面非定常压差系数。非定常压差系数定义为为翼型表面压差一阶谐波分量。图中将谐波平衡方法的计算结果与文献［15］中的利用线性理论计算出的结果进行了对比，其吻合程度较好。

2.3 某压气机叶栅气动弹性分析

利用本文的谐波平衡方法对某压气机典型截面叶栅气弹稳定性进行了分析。压气机叶型如图5所示，其弦长c=0.0777m，安装角γ=46.29°，稠度τ= 2.55。其计算条件为：进口马赫数M1=0.75，进气角（与轴向夹角）αm=52°，进口总压p*=7042.13Pa，进口总温T*=232.26K，出口背压pb=4998.9Pa。

图5 压气机叶型Fig.5 The compressor arifoil

叶片发生扭转振动，扭转中心位于叶片前缘，振动扭转角度幅度为α=3°，相邻叶片振动相位差σ= 0°，折合频率k=0.222。计算采用二阶谐波格式，一个周期内等时间距选择五个时间层。

为了研究叶片的气弹稳定性，定义非定常力矩系数：

图6为计算得到的非定常压差系数和非定常力矩系数虚部沿弦向的分布曲线。由图6可知，此叶栅在相位差为0°时，气动力在叶表大部分区域做负功，仅在前缘和尾缘附近做正功。

图6 压气机叶型非定常力矩系数Fig.6 Unsteady moment coefficient distribution for compressor airfoil

图7为定常计算得到的叶栅通道马赫数云图和流线图，图8～图11分别为0T，1／4T，1／2T 和3／4T时，叶栅通道马赫数云图和流线图。由图可见，在定常状态时，叶型吸力面并没有发生分离；当叶片发生振动时，在任何时刻，叶型吸力面总是存在分离涡。这说明，叶片一旦发生振动，很容易在其吸力面产生振动诱导涡，从而致使压气机的气动性能下降。从非定常流动瞬时流线图可以看出，在叶型吸力面，一般

图7 定常计算叶栅通道马赫数云图及流线图Fig.7 Steady flow field around the cascades

图8 0T时刻马赫数分布云图及流线图Fig.8 Unteady flow field around the cascades（0T）

图9 1／4T时刻马赫数分布云图及流线图Fig.9 Unteady flow field around the cascades（1／4T）

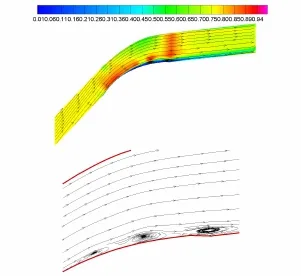
图10 1／2T时刻马赫数分布云图及流线图Fig.10 Unteady flow field around the cascades（1／2T）

图11 3／4T时刻马赫数分布云图及流线图Fig.11 Unteady flow field around the cascades（3／4T）

存在两个分离涡，在1／2T 时刻，存在三个分离涡。这说明，振动诱导的分离涡产生的频率大于振动的频率，在一个振动周期，可产生若干个分离涡。对不同时刻的流线图进行对比可以看出，在瞬时迎角较小的1／4T时刻，吸力面依然存在两个分离涡，而在0T 时刻，吸力面上一个分离涡已经运动到尾缘处，即将脱落，其流场品质比1／4T 时刻稍好。因此，在振动情况下，瞬时迎角较小，并不代表其流场品质较好，流场结构与分离涡产生的频率有很大关系。

为了对压气机叶栅的气弹特性进行全面分析，本文计算了相邻叶片振动相位差σ=30°，60°，90°，120°，150°，180°，210°，240°，270°，300°和330°时的非定常流场，计算得到了不同振动相位差时叶栅非定常力矩系数CM，如图12所示。

由图12可以看出，本叶栅气弹失稳可能性最大的点并不在σ=0°处。因此，在叶轮机械气弹稳定性分析时，需对其不同振动相差情况进行分析，以便准确把握其气动弹性特性。此外，从图中可知，本叶栅在振动相位差位于18°～166°之间时，有可能发生气弹失稳。

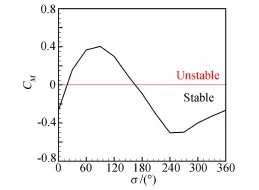
图12 压气机叶栅非定常力矩系数随相邻叶片振动相位差变化情况Fig.12 Unsteady moment coefficient of compressor airfoil at different interblade phase angles

3 谐波阶次对计算效率的影响

在计算非定常流动时，本文所采用的计算方法一个周期内最少可以只设置三个时间层来计算，即一阶谐波格式。为了研究谐波平衡方法阶次对计算效率的影响，本文分别针对2.1节的NACA0012组成的叶栅算例采用不同阶次的谐波平衡方法进行计算。

图13是分别采用一阶、二阶、三阶、四阶谐波平衡方法计算得到的叶栅表面非定常压差系数。由图可见，采用不同阶次的方法计算结果几近完全相同。

图13 不同阶次谐波平衡方法非定常压差系数比较Fig.13 Comparison of unsteady pressure jump coefficient for different number of harmonics

表1是不同阶次谐波平衡方法的计算耗时对比。在这里假设定常计算所用时间为1，不同阶次谐波平衡方法计算耗时与定常计算耗时的比值即为无量纲计算耗时。定常计算与非定常计算取同样的计算步数，均推进4000步。

表1 不同阶次谐波平衡方法计算耗时对比Table 1 Comparisonof computational effiency for different number of harmonics

由表1可见，前三阶格式的谐波平衡方法计算耗时与定常计算处于同一量级。而其他学者认为，采用时域方法的计算耗时要比谐波平衡方法的计算耗时高一到两个量级。由于计算所采用的收敛评判角度不同，因此无法做出准确对比。但从本文计算过程来看，单通道计算时，谐波平衡方法的计算效率确实相当高，时域方法计算耗时约为二阶谐波平衡方法计算耗时的20～30倍左右，可见二阶谐波平衡方法的计算效率要比时域方法的计算效率高一个量级。如果存在相位差时，采用多通道的时域计算方法将因为计算区域成倍增加而使得计算耗时也几乎成倍增加。因此，在存在相位差时，采用谐波平衡方法的计算效率比时域法的计算效率可以高达两个量级。另外，从不同阶次的谐波平衡方法耗时对比来看，阶次每高一阶，其耗时平均增加2.39。因此，在非定常流计算时，应根据计算对象的不同，选择适当的谐波平衡方法，既保证精度要求，又能提高计算效率。

4 结 论

本文发展了基于谐波平衡方法计算振荡叶栅非定常流动的程序，通过算例对这种方法进行了验证，得出以下结论：（1）通过谐波平衡方法与双时间方法的计算结果对比表明，两种计算方法得到的翼型表面一阶非定常压力系数分布和升力系数吻合的非常好，从而验证了程序的可靠性和谐波平衡方法的准确性。（2）通过计算对比证明谐波平衡方法是一种非常高效的非定常流计算方法，本文二阶谐波平衡方法的计算效率比双时间方法高一个量级，因此可以广泛应用于周期性非定常流动数值模拟当中。（3）对于周期性较强的非定常流动，可以采用较少的阶次就可以满足计算精度，可大大提高计算效率。（4）从压气机叶栅气弹稳定性分析结果来看，气弹失稳点不一定在0°相位差处。因此，在气弹稳定性分析时，要对不同相差情况进行分析。

［1］ JAMESON A.Time dependent calculations using multigrid，with applications to unsteady flows past airfoils and wings［A］.AIAA 10th Computational Fluid Dynamics Conference［C］.Honolulu，Hawaii，1991.

［2］ HU Y C，ZHOU X H.Application of dual-time stepping method to calculating unsteady viscous flow around oscillating cascade［J］.Journal of Northwestern Polytechnical University，2003，21（3）：269-272.（In Chinese）胡运聪，周新海.振荡叶栅粘性非定常绕流计算的双时间法［J］.西北工业大学学报，2003，21（3）：269-272.

［3］ VERDON J M，CAPAR J R.Development of a linear unsteady aerodynamic analysis for finite-deflection subsonic cascades［J］.AIAA Journal，1982，20（9）：1259-1267.

［4］ WHITEHEAD D S.A finite-element solution of unsteady twodimensional flow in cascades［J］.International Journal for Numerical Methods in Fluids，1990，10（1）：13-34.

［5］ HALL K C，CLARK W S.Linearized euler predictions of unsteady aerodynamic loads in cascades［J］.AIAA Journal，1993，31（3）：540-550.

［6］ HALL K C，LORENCE C B.Calculation of three-demension unsteady flows in turbomachinery using the linearized harmonic euler equations［J］.Journal of Turbomachinery-Transactions of ASME，1993，15（4）：800-809.

［7］ EKICI K，VOYTOVYCH D M，HALL K C.Time-linearized navier-stokes analysis of flutter in multistage turbomachines ［A］.43rd AIAA Aerospace Sciences Meeting and Exhibit［C］.Reno，NV，2005.

［8］ HALL K C，THOMAS J P，Cl ARK W S.Computation of unsteady nonlinear flows in cascades using a harmonic balance technique［J］.AIAA Journal，2002，40（5）：879-886.

［9］ EKICI K，HALL K C.Nonlinear analysis of unsteady flows in multistage turbomachines using the harmonic balance technique ［A］.44th AIAA Aerospace Sciences Meeting and Exhibit［C］.Reno，NV，2006.

［10］EKICI K，HALL K C.Nonlinear analysis of unsteady flows in multistage turbomachines using harmonic balance［J］.AIAA Journal，2007，45（5）：1047-1057.

［11］EKICI K，KIELB R E，HALL K C.The effect of aerodynamic asymmetries on turbomachinery flutter［A］.47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition［C］.2009，Orlando，Florida.

［12］THOMASJ P，CUSTER C H，DOWELL E H，et al.F-16 fighter aeroelastic computations using a harmonic balance implementation of the OVERFLOW 2 Flow Solver［A］.51st AIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics，and Materials Conference［C］.2010，Orlando，Florida.

［13］YANG Q Z，SHI Y Q，HUANG X Q，et al.Numerical analysis of three-dimensional unsteady flow around oscillating cascades ［J］.ACTA Aerodynamica Sinica，2006，24（1）：62-65.（In Chinese）杨青真，施永强，黄秀全，等.振荡叶栅三维非定常流动数值分析［J］.空气动力学学报，2006，24（1）：62-65.

［14］HUFF D L.Numerical simulations of unsteady，viscous，transonic flow over isolated and cascaded airfoils using a deforming grid［A］.AIAA 19th Fluid Dynamics，Plasma Dynamics and Lasers Conference［C］.1987／Honolulu，Hawaii.

［15］HE L.An Euler solution for unsteady flows around oscillating blades ［J］.Transactions of American Society of Mechianical Engineers：Journal of Turbomachinery，1990，112（4）：714-722.

A numerical approach for fast simulation of unsteady flow around oscillating cascades

SHI Yongqiang，YANG Qingzhen，HUANG Xiuquan，GUO Xiao

（School of Power&Energy，Northwestern Polytechnical University，Xi’an 710072，China）

A harmonic balance method for the analysis of nonlinear unsteady flow around oscillating cascades is developed to improve computational efficiency for the simulation of periodic flow in turbomachinery.The periodic unsteady flow parameters can be represented by a Fourier series.In this way，the unsteady problem can be solved using conventional computational fluid dynamic method for steady problem.The analysis exploits the fact that，calculated results by harmonic balance are in good agreement with those from dual-time stepping method and linear method，and present method is highly efficient；it is about one order of magnitude faster than conventional dual-time stepping method in the present computation.The effects of the number of harmonics are also studied.It shows that lower order harmonic balance methods are sufficient to simulate periodic unsteady flow accurately except the flow fields including serious separated domain.So，lower order harmonic balance methods could be adopted to analysis unsteady flow in turbomachinery to reduce the computational cost.In addition，the characteristic of unsteady flow around a compressor cascade is investigated，and the mechanism of generation of separated vortex and the vortex shedding frequency are also analyzed.

oscillating cascade；harmonic balance method；unsteady flow；dual-time stepping method；shape correction method

V221.3

Adoi：10.7638／kqdlxxb-2012.0146

0258-1825（2014）04-0481-07

2012-09-06；

2013-02-25

国家自然科学基金（50376053，50706039，11302179）；陕西省自然科学基础研究基金（2013JQ1009）；西北工业大学基础研究基金

（JC201245）

施永强（1980-），男，甘肃平凉人，副教授，博士，研究方向：叶轮机气动热力学.E-mail：yqshi＠nwpu.edu.cn

施永强，杨青真，黄秀全，等.一种快速模拟振荡叶栅非定常流的数值方法［J］.空气动力学学报，2014，32（4）：481-487.

10.7638／kqdlxxb-2012.0146. SHI Y Q，YANG Q Z，HUANG X Q，et al.A numerical approach for fast simulation of unsteady flow around oscillating cascades［J］.ACTA Aerodynamica Sinica，2014，32（4）：481-487.