串列叶栅和叶片弯曲对角区失速和叶尖泄漏流的耦合作用*

高 玺 曹志远 邓莉平 宋 澄 张 翔

（1.西北工业大学动力与能源学院；2.四川轻化工大学）

0 引言

级负荷的不断增大是现代多级压气机的发展趋势[1]。在高负荷压气机叶片吸力面/端壁区域存在的三维角区分离或角区失速，是影响压气机效率和稳定性的重要原因之一[2-3]。

串列叶片的应用是控制叶片吸力面流动分离的有效方法之一，基本原理是附面层会在串列叶片后叶排重新生成，因此，串列叶片在增大负荷的同时不会产生大的流动分离[4]。串列叶片不仅可以控制流动分离，还可以通过增大气流转折角来增大压气机的级负荷，减小压气机的轴向距离[5]。Liu[6]等通过比较单叶片结构和串列叶片结构得到了高转角串列叶片的设计方法，合理的设计能使串列叶片在实现高转角、高压比的同时，获得比单叶片结构更高的效率。Donald[7]等对某跨音速串列转子进行了一系列试验，该转子在设计点的效率可以达到0.88，总压升为1.77。Weber[8]等设计了1:2 形式的跨音速串列叶栅并进行了优化与分析，试验表明，最优设计可以实现60°以上的转折角、1.75 的静压升以及较低的总压损失。Hergt[9]等在总结现有跨音速串列叶栅的基础上，设计并优化一种新型跨音速串列叶栅，并做了实验研究。结果表明利用现代设计方法有可能实现高负荷、高效率的跨音速串列叶栅的设计，同时提出串列叶栅中的三维流动和二维流动效应应该成为未来的研究重点。

虽然串列叶片能实现更高的级负荷，但仍有角区分离存在，并且会存在与一般叶栅不同的泄漏流结构[10-11]。McGlumphy[12]等在研究中提到在串列转子前叶排和后叶排的端壁/吸力面角区存在回流，会限制串列转子效率的提升。Zhang[13]等在串列叶栅耦合端壁抽吸的研究中发现在串列叶栅前叶片通道中会有严重的角区失速。Kumar[14]等在对串列转子的试验研究中发现串列转子会在前叶排和后叶排分别形成一个泄漏涡，并且会在下游汇合成一个更大的涡。Han[15]等发现跨音速串列转子的失速主要与叶尖泄漏流和靠近叶尖的间隙喷射有关，且前叶排的间隙大小是影响串列转子失速的主要因素。目前针对串列叶栅角区分离与叶尖泄漏流的研究较少，对其流动机理认识还不清楚，需要进一步的研究。

目前针对改善串列叶栅流场控制技术的研究较少，现有的方法包括端壁抽吸[13]、弯掠和倾斜叶片优化[16]等技术。

叶片弯曲作为一种能控制角区分离的被动控制方法，已经得到了广泛的研究[17]。现有研究表明叶片弯曲可以改变叶片静压分布、控制二次流来达到控制压气机内流动分离的目的[18-20]。Kan[21]等对叶片弯曲对角区失速的控制研究中发现弯曲叶片通过改变叶栅的压力梯度来控制叶栅中涡结构的影响范围，改变涡结构向低能流体的输运过程，进而影响流动损失的质量流量分布。Weingold[22]等通过对某压气机的数值模拟和实验,考察了弯曲静叶对压气机静子端壁损失的影响。结果表明,弯曲静子在流场中产生的径向力延缓和消除角区分离的形成，进而减小损失，增大转折角。Seo[23]等应用弯掠耦合，提高了某低速风扇的总效率，同时也明显提高了该风扇在非设计点的性能。Cao[24]等为了提高高负荷压气机叶栅的性能，研究了正反弯对流场的影响，结果表明，正弯能有效控制角区分离，但会使叶中流场恶化。虽然弯曲技术已经在单叶片中得到了广泛的研究，但是目前仅在Zhang[16]的研究中看到了三维叶片技术在串列叶栅中的应用。从现有文献来看，弯曲叶片在串列叶栅中的应用还很少见，串列叶片耦合弯曲能否在增大级负荷的同时，降低角区分离需要进一步研究。叶片弯曲可以改变叶片端壁负荷，从而影响泄漏流的结构，串列叶片的泄漏流结构又与一般叶栅不同，因此串列叶片耦合弯曲对泄漏流结构的影响也需要进一步研究。

串列叶片能有效增大压气机的级负荷，但是角区分离等会限制串列叶片效率和负荷的进一步提升，而叶片弯曲能抑制角区分离。为了能在增大叶片负荷的同时，降低角区分离带来的损失，串列叶片耦合弯曲的研究是十分必要的。本文主要的研究内容是串列叶片耦合弯曲对角区分离和泄漏流的影响。

1 串列叶栅的几何参数及气动参数

本文研究的原始高负荷串列叶栅的几何定义如图1 所示，表1 给出的是串列叶栅的几何参数和气动参数。本文中串列叶栅的数值模拟的设计进口马赫数为0.6，雷诺数为8×105。二维设计工况下原始串列叶栅的扩散因子为0.59。

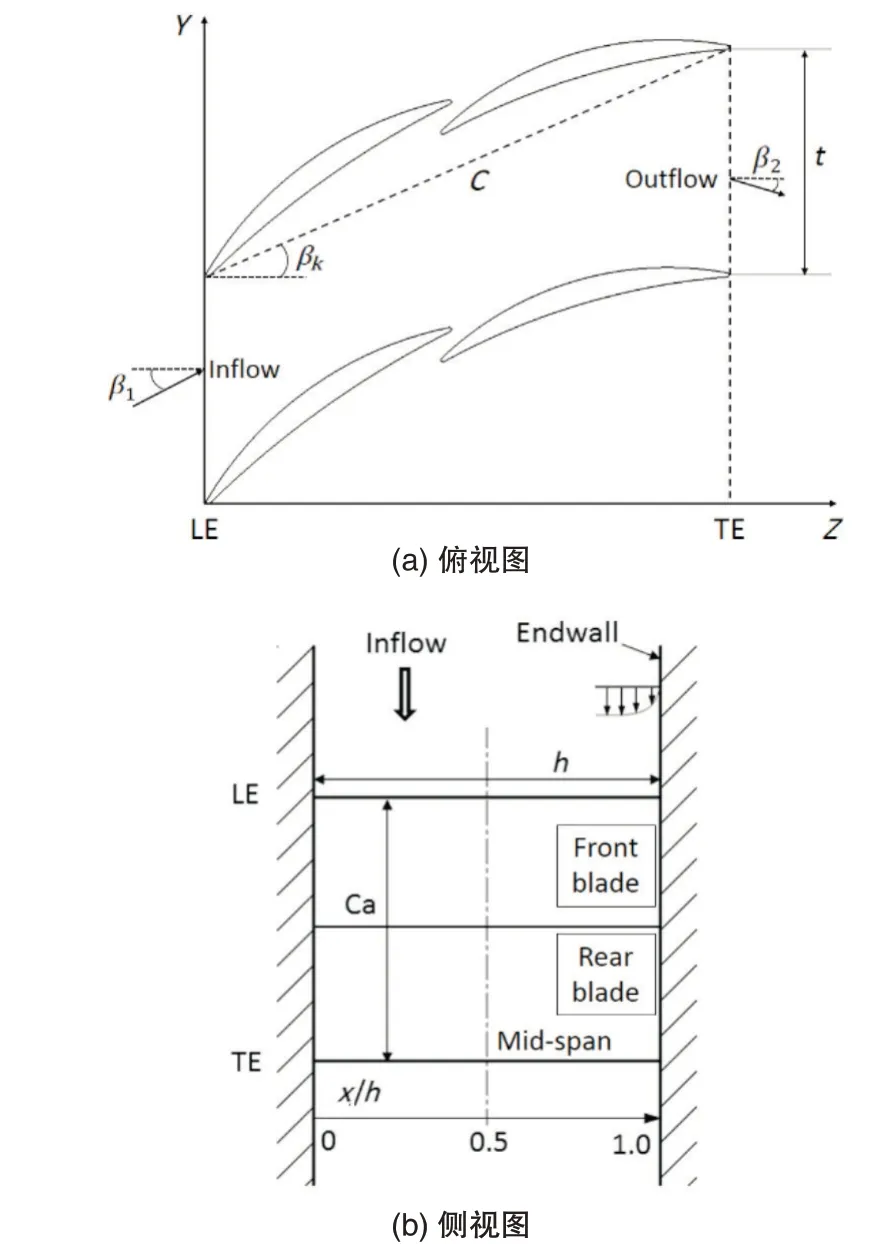
图1 串列叶栅几何及定义Fig.1 Schematic and definitions of tandem cascade

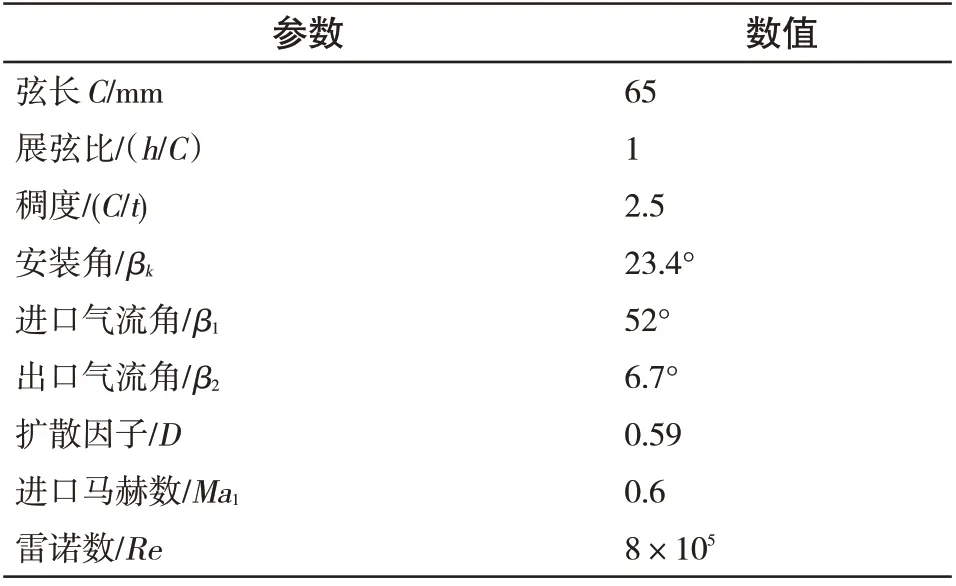
表1 几何及气动参数Tab.1 Geometric parameters and aerodynamic parameters

2 数值模拟方法和试验验证

本文基于周期性假设，对高负荷串列叶栅进行了单通道的数值模拟研究。叶栅通道网格采用NUMECA FINE/TURBO软件包中的AUTOGRID生成的“O-4H”网格拓扑结构，叶片附近和叶尖间隙处采用“O”型网格。串列叶栅数值模拟域的进口设置为叶栅前缘上游1 倍轴向弦长处，出口设置为叶栅尾缘下游2 倍轴向弦长处。叶栅网格拓扑如图2所示。

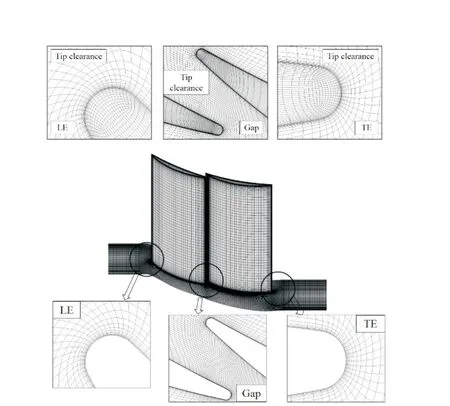
图2 串列叶栅叶片吸力面/端壁/叶尖间隙网格Fig.2 Blade&endwall surface/Tip clearance mesh of baseline tandem cascade

本文数值模拟采用的湍流模型是SST K-ω 模型。进口边界给定总温、总压、进口气流角和1%的湍流强度，出口边界采用静压。

如图3 所示，串列叶栅叶片表面和近端壁的y+在1附近，表明叶栅近壁面的网格尺寸符合所选湍流模型的要求。

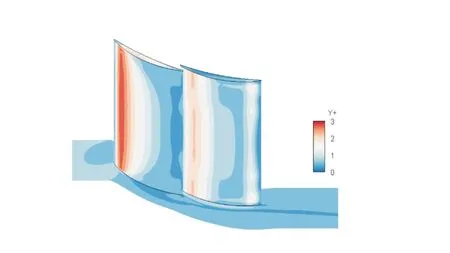
图3 串列叶栅叶片表面和端壁y+云图Fig.3 y+contours near blade and endwall surfaces of baseline tandem cascade

为了检验网格无关性，对不同网格数的原始串列叶栅进行数值模拟，选用的网格数范围为50 万到700万。图4比较了不同网格数叶栅的总压损失系数，总压损失系数以300 万网格叶栅的总压系数为基准进行了归一化处理，结果表明网格数超过200 万时，随着网格数增大，总压损失系数变化不大。经过网格无关性校验，本文选用的叶栅网格数为300万。式1给出了总压损失系数的定义，Pt1是叶栅进口总压，Pt2是叶栅出口总压（本文计算叶栅总压损失的出口截面选为串列叶栅尾缘下游1倍轴向弦长处），P1是叶栅进口静压。

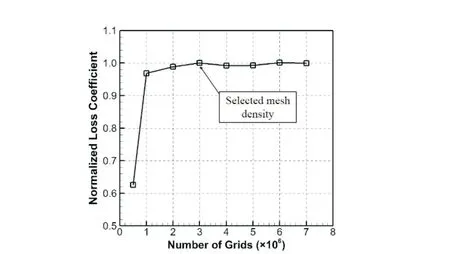
图4 网格无关性验证Fig.4 Validations of grid independence

本文研究的是自行设计的串列叶栅，缺乏实验数据。因此，本文对南京航空航天大学徐雕[25]的串列叶栅进行数值模拟并进行验证。串列叶栅表面静压系数（Cp）的数值模拟结果和试验结果的比较如图5 所示。结果表明，数值模拟结果和试验结果比较吻合，说明本文采取的数值模拟方法是比较准确的。表面静压系数的定义如式2所示，Pt1是叶栅进口总压，P1是叶栅进口静压，ρ1是叶栅进口气流密度，V1是叶栅进口气流速度。

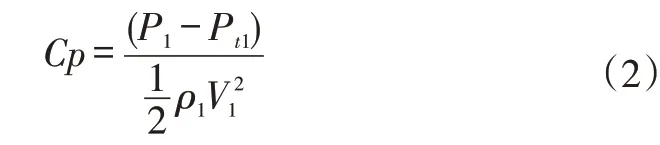
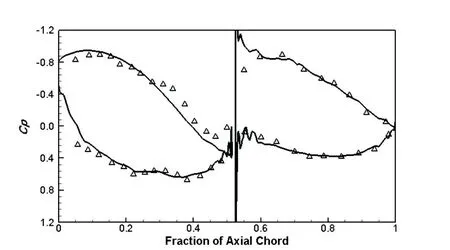
图5 原始串列叶栅数值模拟和试验结果对比[25]Fig.5 Comparison of numerical results and experimental results of baseline tandem cascade[25]

3 串列叶栅的弯曲设计

本文为了探究叶片弯曲和串列叶栅对叶栅流场的耦合作用，在保持串列原始叶栅不变的基础上，设计两种正弯弯角，分别为20°和40°。弯角的定义如图6 所示，叶片从吸力面朝着压力面的弯曲定义为正弯。

本文在图6 的基础上，针对不同弯角的叶片，还设计了只让前排叶片弯曲（F）和只让后排叶片弯曲（A）两种不同的弯曲形式，研究不同弯角、不同弯曲形式对串列叶栅流场的影响规律。

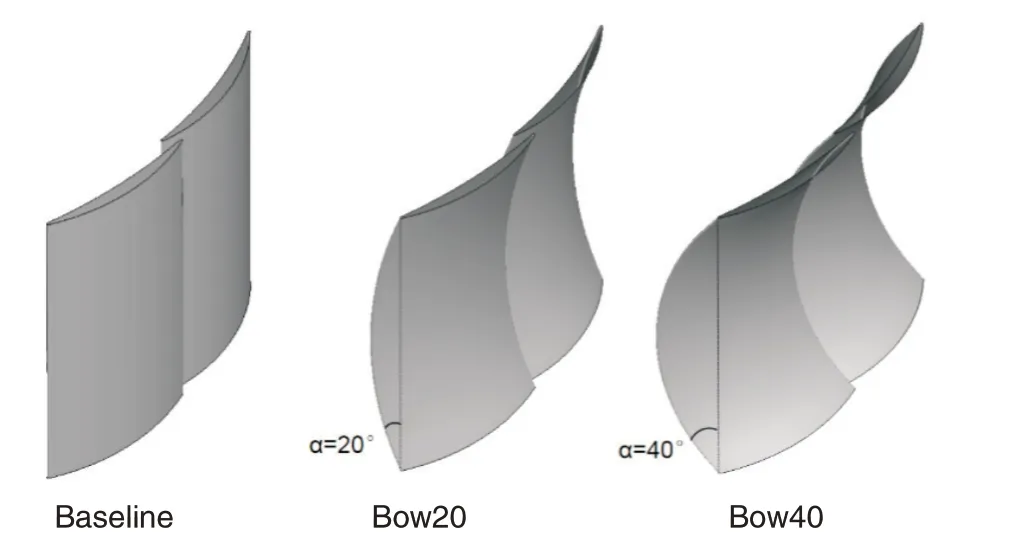
图6 串列叶栅几何示意图Fig.6 Geometry of tandem cascades

4 结果与讨论

4.1 叶片弯曲对不带叶尖间隙串列叶栅流场的影响

从图7叶栅总压损失系数图中可知，叶片弯曲能有效降低叶栅的总压损失，Bow20工况使总压损失降低了37.6%。图7中的总压损失是以原始叶栅的总压损失为基准，负值表示总压损失低于原始叶栅的数值，正值与之相反。为了进一步研究叶片弯曲对不带叶尖间隙串列叶栅流场的影响，本节研究了原始叶栅、叶片弯角为20°（Bow20）和叶片弯角为40°（Bow40）三个串列叶栅的流场。

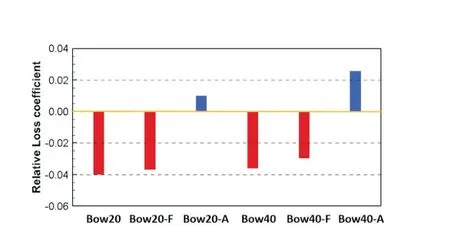
图7 相对总压损失系数Fig.7 Relative total pressure loss coefficient

在原始的直列叶栅中（图8（a）），静压系数云图等值线在靠近吸力面处是弯曲的，且靠近吸力面处端壁静压大于叶栅中部。叶片正弯曲后（图8（b）和图8（c）），静压系数云图的等值线几乎是直的且垂直于端壁，叶片吸力面压力分布呈两端高，中间低的“C”型分布。从静压系数云图可知，20°正弯后，叶中负荷较原始增大。

图8 8.4%轴向弦长处静压系数云图Fig.8 Static pressure coefficient counters at 8.4%axial chord

图9 展示的是不同工况下串列叶栅近端壁和吸力面处的静压系数云图和极限流线。在原始叶栅中，串列叶栅前排叶片存在严重的角区失速，从吸力面和端壁极限流线可知，在前排叶片角区有回流现象。从吸力面静压系数云图可知，在前排叶片尾缘处，由于角区失速的存在，叶中静压大于端壁。在后排叶片吸力面处几乎没有分离，这是由于两排叶片间隙的射流使后排叶片表面附面层重新生成。

叶片正弯能有效抑制角区失速的发生，两个叶片都弯曲，且弯角为20°时，叶栅总压损失最大降低了37.6%。叶片正弯曲后（图9（b）和图9（c）），端壁回流消失，前排叶片吸力面角区分离线几乎消失，表明吸力面角区失速得到有效的抑制；但叶栅前排叶片尾缘分离线前移，表明前排叶片尾缘分离明显增大。由静压系数云图可知，弯角越大，叶片正弯对吸力面沿叶展的静压系数分布与端壁横向压力梯度影响越大。弯角为40°时，叶栅前排叶片尾缘端壁静压大于叶中静压，且端壁二次流强度也大于原始叶栅和Bow20 工况。虽然叶片正弯后端壁二次流强度增大，但是并未引起比较严重的角区失速，这是由于叶片正弯后增大了吸力面与端壁的夹角，减弱了端壁低能流体与吸力面低能流体在角区处的堆积，从而有效抑制了角区分离的再次形成。

图9 串列叶栅吸力面和端壁静压系数云图和极限流线Fig.9 Static pressure coefficient&limiting streamlines on suction surface and endwall of tandem cascade

不同工况下串列叶栅端壁和叶中的表面静压系数分布如图10到图12所示。叶片弯曲对叶片沿展向的压力梯度有明显的作用。弯角越大，展向的压力梯度越大。

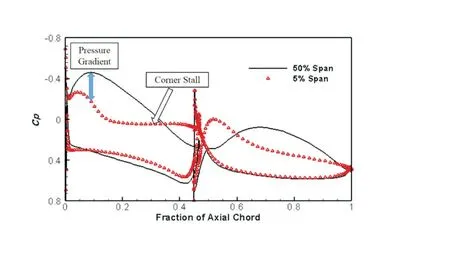
图10 表面静压系数分布（Baseline）Fig.10 Static pressure coefficient distribution

图11 表面静压系数分布（Bow20）Fig.11 Static pressure coefficient distribution（Bow20）

图12 表面静压系数分布（Bow40）Fig.12 Static pressure coefficient distribution（Bow40）

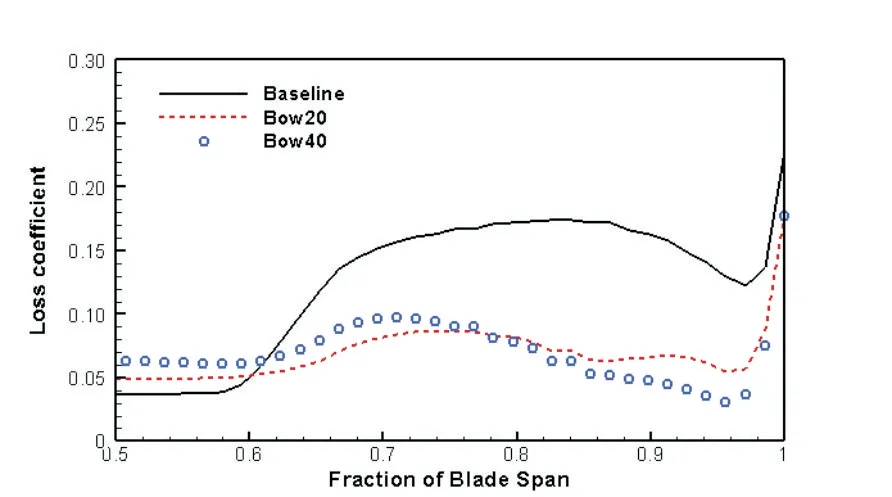
图13 叶栅尾缘下游50%轴向弦长处损失系数沿展向分布Fig.13 Loss coefficient distribution along spanwise at 50%axial chord downstream of cascade trailing edge

图13是叶栅尾缘下游50%轴向弦长处损失系数沿叶展的分布。因为叶片弯曲能有效降低叶栅前排叶片处的角区失速，所以图13中0.6到1叶展处的总压损失系数明显降低，且弯角越大，靠近端壁处的总损失降低得越多，叶中损失增大得越多。这是因为随着角区失速的抑制，前排叶片及叶栅的扩压能力都增大，因此前排叶片尾缘分离增大。

由于角区失速的存在，原始叶栅（图14（a））尾缘下游50%轴向弦长处存在很大的低速区。采用弯曲叶片后（图14（b）），角区低速区范围明显减小，但由于叶栅前排叶片尾缘分离的增大，叶中低速区范围增大。叶片弯曲影响了整个叶栅的速度分布，由于角区失速得到抑制，整个叶栅的流通能力增强，主流区马赫数相比于原始叶栅减小，叶栅的扩压能力增强。

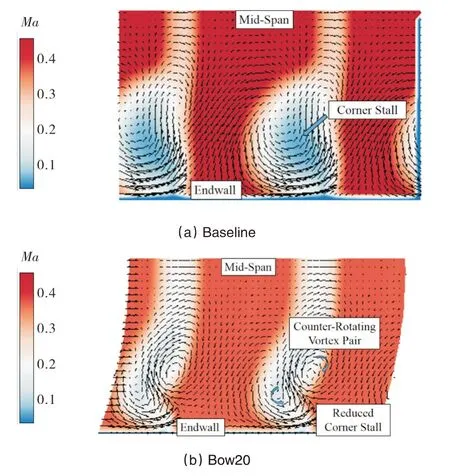
图14 叶栅尾缘下游50%轴向弦长处马赫数云图和二次流Fig.14 Mach number contours and secondary flow vectors at 50%axial chord downstream of cascade trailing edge

4.2 不同弯曲方案对不带叶尖间隙串列叶栅流场的影响

本节研究了串列叶栅中只有一个叶片采用弯曲对叶栅流场的影响。由于两个叶片都采用20°弯角时能取得较好的控制效果，本节采用20°弯角，对串列叶栅只有一个叶片弯曲对串列叶栅流场的影响进行研究，前叶排弯曲的工况为Bow20-F，后叶排弯曲的工况为Bow20-A。

与图8（a）的原始叶栅相比，后排叶片弯曲的Bow20-A工况的静压系数云图与等值线变化不大，而前排叶片弯曲的Bow20-F 工况与图8（b）相似，说明只有后排叶片弯曲对前排叶片的流场影响不大。

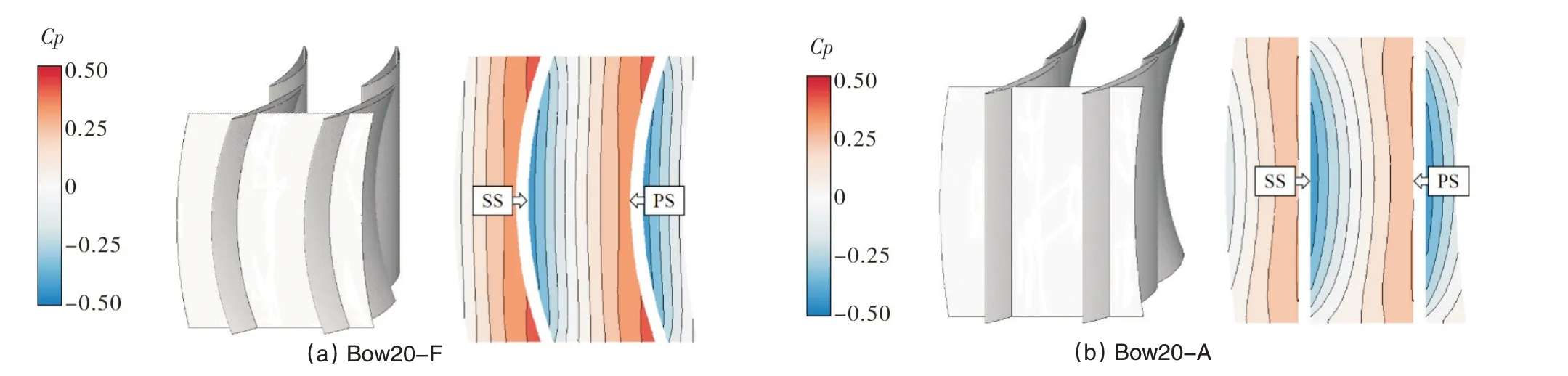
图15 8.4%轴向弦长处静压系数云图Fig.15 Static pressure coefficient counters at 8.4%axial chord

与图9（b）相比，只有前排叶片弯曲的Bow20-F 工况（图16（a））也能有效抑制前排叶片通道中的角区失速，但是后排叶片角区部分会产生强于Bow20工况的角区分离。这是由于前排叶片弯曲后，端壁二次流增强，而后叶排未弯曲，因此后排叶片端壁低能流体在角区处的堆积加剧，从而产生较弱的角区分离，而后排叶片也弯曲后会抑制新产生的角区分离，使得叶栅的损失进一步降低。

与图9（a）相比，只有后排叶片弯曲的Bow20-A工况（图16（b））对前排叶片的影响较小，虽然略降低了前排叶片的尾缘分离，但不能控制前排叶片通道中的角区失速，还会加剧后排叶片的尾缘分离，从而使叶栅的损失增大。

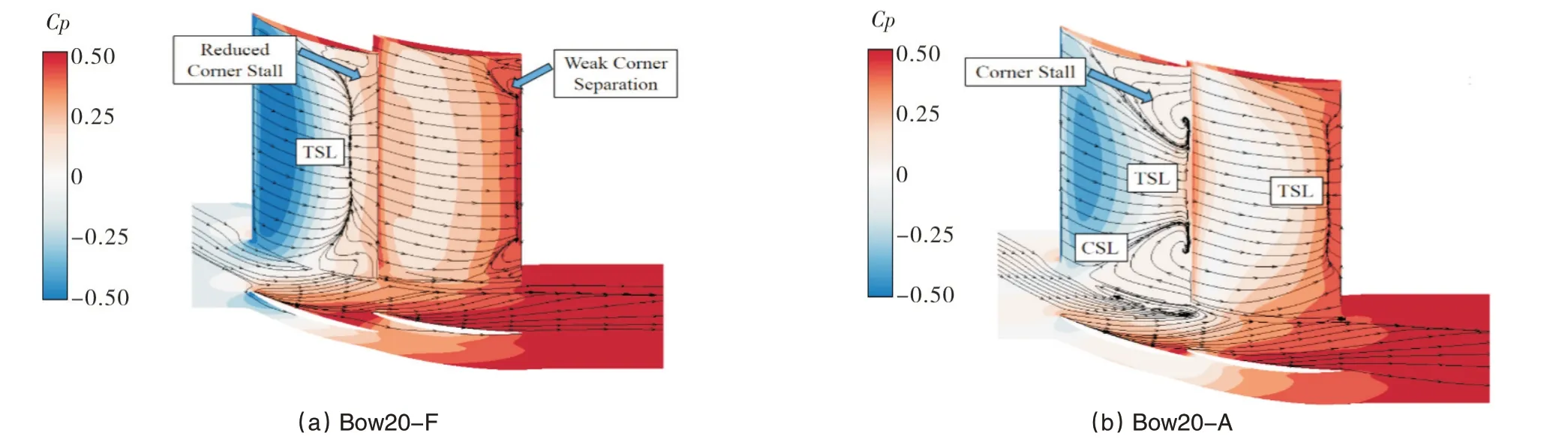
图16 串列叶栅吸力面和端壁静压系数云图和极限流线Fig.16 Static pressure coefficient&limiting streamlines on suction surface and endwall of tandem cascade

由图17（a）不同工况下50%叶展处的表面静压系数分布可知，Bow20-F工况叶中静压分布与Bow20工况的叶中静压分布相似。Bow20-A 工况对前排叶片叶中的静压分布影响不大，只是使前排叶片尾缘的负荷降低，从而使前排叶片尾缘分离稍有降低。Bow20-A工况主要是使得后排叶片叶中负荷增大，增大了后排叶片叶中的逆压梯度，使得后排叶片尾缘流场恶化。

由5%叶展处的静压系数分布图（图17（b））可知，Bow20-F 工况前排叶片的叶中静压分布与Bow20 工况的叶中静压分布相似，前排叶片尾缘受后排叶片影响较大。Bow20工况由于后排叶片也是弯曲的，后排叶片5%叶展处的负荷低于Bow20-F 工况，因此后排叶片角区分离会更小一些。相比于原始工况，Bow20-A工况对近端壁静压分布影响较小。

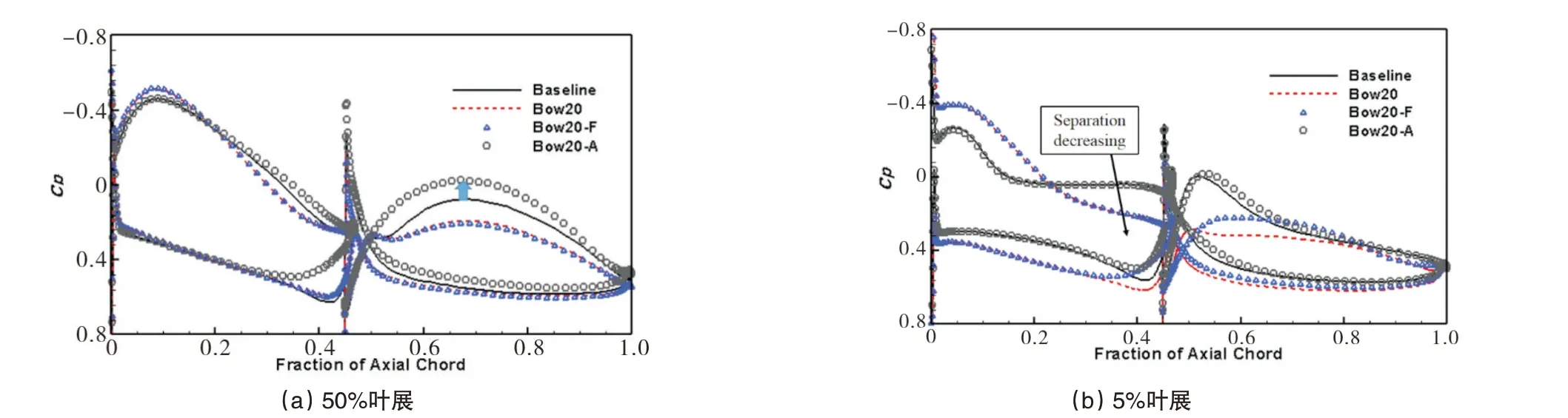
图17 静压系数分布Fig.17 Static pressure coefficient distribution

由图18 损失系数沿叶展分布可知，Bow20-F 工况已经可以有效降低近端壁处的损失。由于Bow20 工况后排叶片的弯曲也抑制了后排叶片新产生的角区分离，Bow20工况能更有效的降低叶栅总损失。Bow20-A工况出口端壁损失增大，并未对前叶排角区失速起到控制作用。

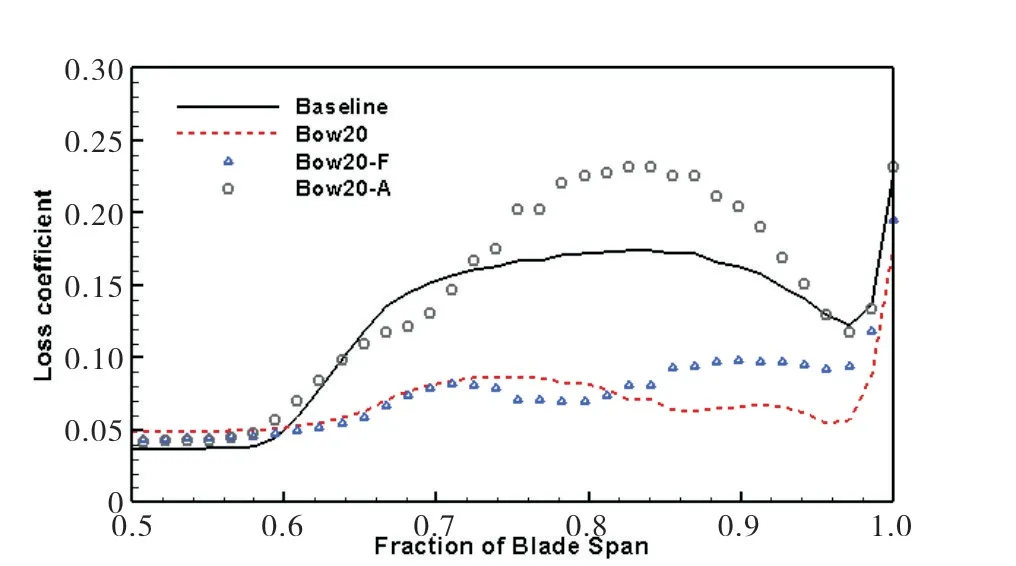
图18 叶栅出口50%轴向弦长处损失系数沿展向分布Fig.18 Loss coefficient distribution along spanwise at 50%axial chord downstream of cascade outlet

从图19的叶栅尾缘下游50%轴向弦长处的二次流和马赫数云图可知，Bow20-F 工况有效减弱了角区失速，使栅后主流区马赫数降低，增大了叶栅的扩压能力。且前叶排弯曲后，前后叶排靠近端壁处的周向距离增大，前叶排主流去一部分流体经间隙从前排叶片压力面流向后排叶片吸力面。这是Bow20-F 工况出口角区内有一小片高速区的原因。

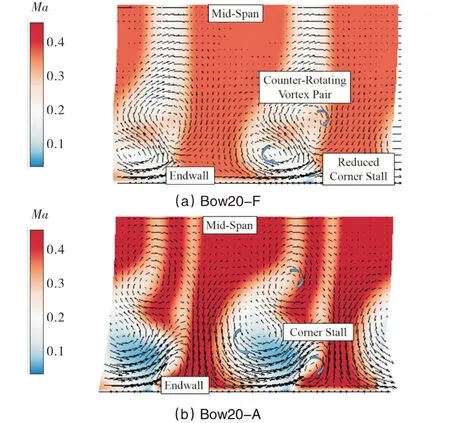
图19 叶栅尾缘下游50%轴向弦长处马赫数云图和二次流Fig.19 Mach number contours and secondary flow vectors at 50%axial chord downstream of cascade trailing edge

Bow20-A工况不能减弱叶栅中的角区失速，栅后主流区马赫数仍很高。由于后排叶片弯曲使得前后叶排叶中的周向间隔增大，前叶排主流一部分流体经间隙从前排叶片压力面流向后排叶片吸力面，使得前后排叶片的尾迹区不能汇合，使叶栅出口形成两个尾迹区，且涡结构变得复杂。

4.3 叶片弯曲对带叶尖间隙串列叶栅流场的影响

本节为了探究叶片弯曲对带叶尖间隙串列叶栅流场的影响，本节对叶尖间隙为0.5mm，1mm 和2mm 的串列叶栅进行了研究，分别命名为T0.5，T1和T2。弯曲叶片选取的弯角为20°（B），弯曲形式为两个叶片都弯曲，本节选取叶栅的攻角都为0°（i0）。

由图20的总压损失比较可知，原始叶栅的叶尖间隙越大叶栅的总压损失越小，但是弯曲后损失降低的也越少。采用叶片弯曲后，BT0.5-i0工况总压损失较T0.5-i0降低27.5%，BT2-i0工况总压损失较T2-i0工况降低3.1%。

图20 损失系数比较Fig.20 Comparison of Loss coefficient

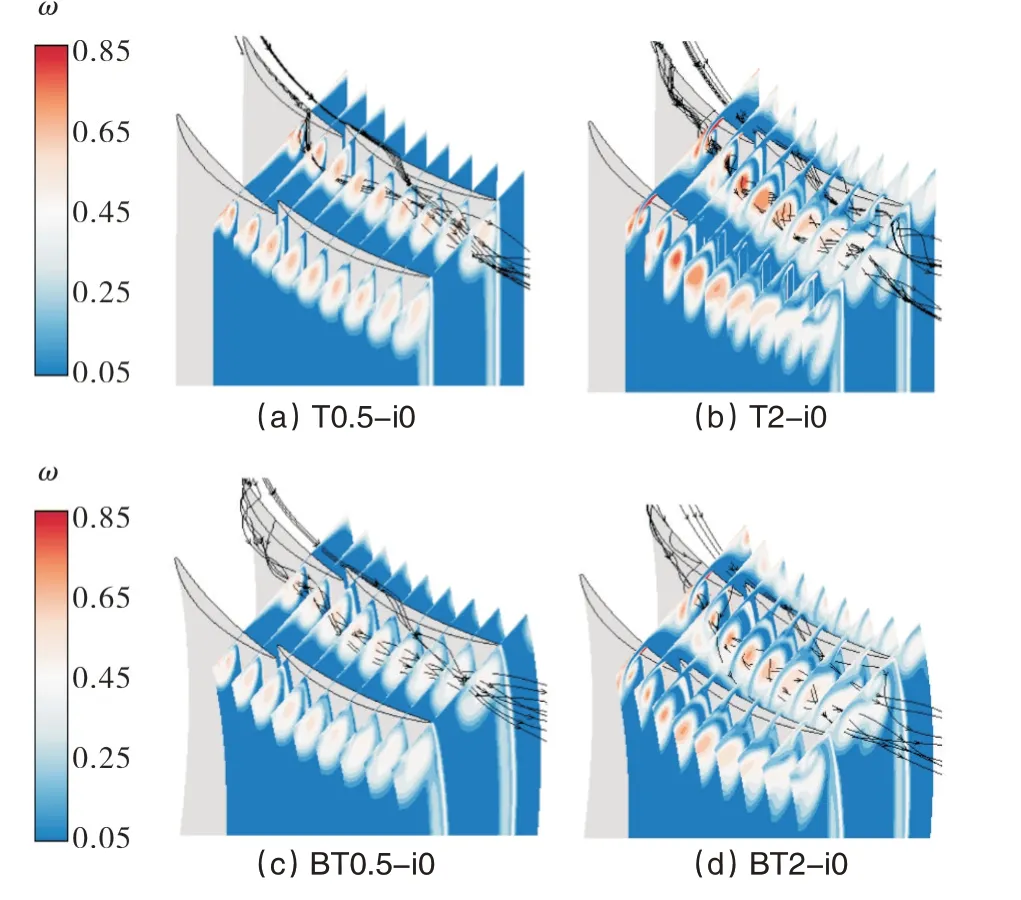
图21 不同轴向弦长处损失系数云图和三维流线Fig.21 Loss coefficient contours at different axial sections and 3D streamlines

从图21 可知叶尖间隙越大，叶栅中的涡系结构越复杂。叶尖间隙为0.5mm时，原始叶栅和弯曲叶栅前后排叶片形成的泄漏流最终会汇聚成一个泄漏涡。而叶尖间隙为2mm 时，结合图22 中T2-i0 工况的三维流线可知，前排叶片的泄漏流会朝着压力面流动，在栅后会与后排叶片的泄漏流汇合成一个靠近压力面的泄漏涡。从图21可知叶片弯曲对泄漏流的影响较小。

图22 三维流线（T2-i0）Fig.22 3D streamlines（T2-i0）

通过图10和图23（a）的比较可知，叶尖泄漏流能有效降低上端壁的角区失速，改善叶栅上端壁的流场。由图23（b）可知，采用弯曲叶片后，由于下端壁处的角区失速得到了抑制，叶中前排叶片尾缘分离区增大。由于泄漏流已经有效控制了上端壁的角区失速，弯曲叶片没有改变上端壁的静压分布，只改变了负荷大小。

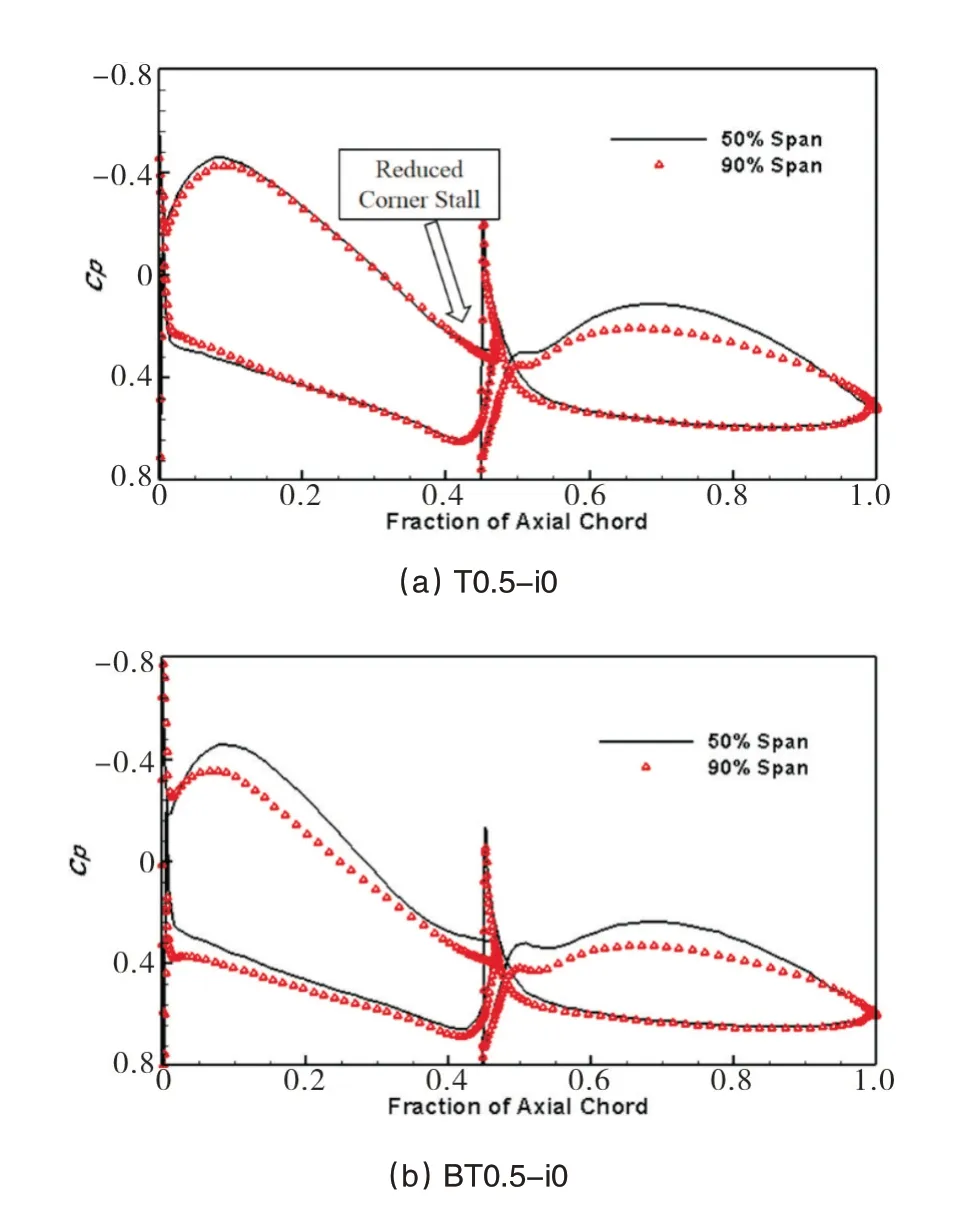
图23 静压系数分布Fig.23 Static pressure coefficient distribution

由图24可知，T2-i0工况虽然由于较大的叶尖间隙会产生的更大的泄漏流损失，但是端壁损失更小。弯曲叶片后下端壁损失明显降低，但上端壁损失略有增大，说明弯曲叶片能有效降低下端壁处的角区失速，但是不能控制泄漏流。

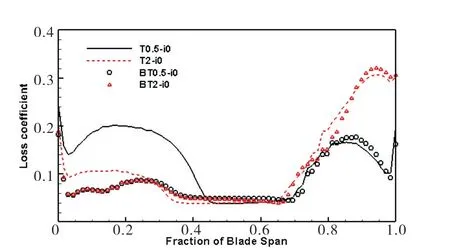
图24 叶栅尾缘下游50%轴向弦长处损失系数沿展向分布Fig.24 Loss coefficient distribution along spanwise at 50%axial chord downstream of blade trailing edge

通过图25（a）和图26（a）比较，叶尖间隙越大，叶栅通道中的涡结构越复杂，0.5mm 叶尖间隙的工况下，有一个泄漏涡和通道涡，且泄漏涡的强度不大。2mm 间隙下，前后叶排泄漏流在靠近压力面处形成泄漏涡，靠近吸力面的是由近端壁的低能流体和一部分泄漏流汇聚成的通道涡，通道涡上部有一个由泄漏涡诱导出来涡。

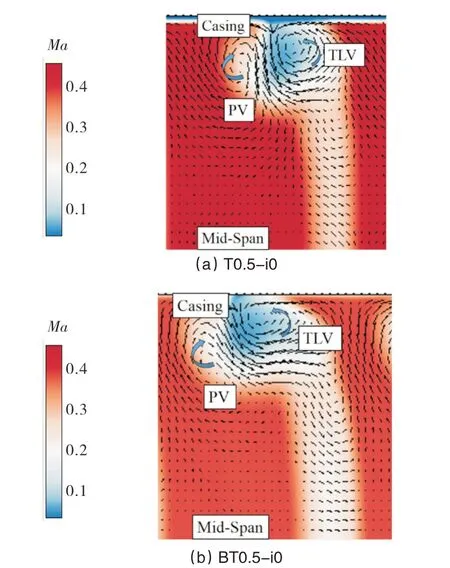
图25 叶栅尾缘下游50%轴向弦长处马赫数云图和二次流（0.5mm）Fig.25 Mach number contours and secondary flow vectors at 50%axial chord downstream of blade trailing edge（0.5mm）

结合图24、图25（b）和图26（b）可知，叶片弯曲后，BT0.5-i0工况的上端壁涡二次流强度都降低，泄漏涡向上端壁移动，使上端壁处损失有所上升，0.7-0.8展向处损失有所降低。BT2-i0工况的泄漏涡朝着压力面和上端壁移动，损失变化与BT0.5-i0工况相似。

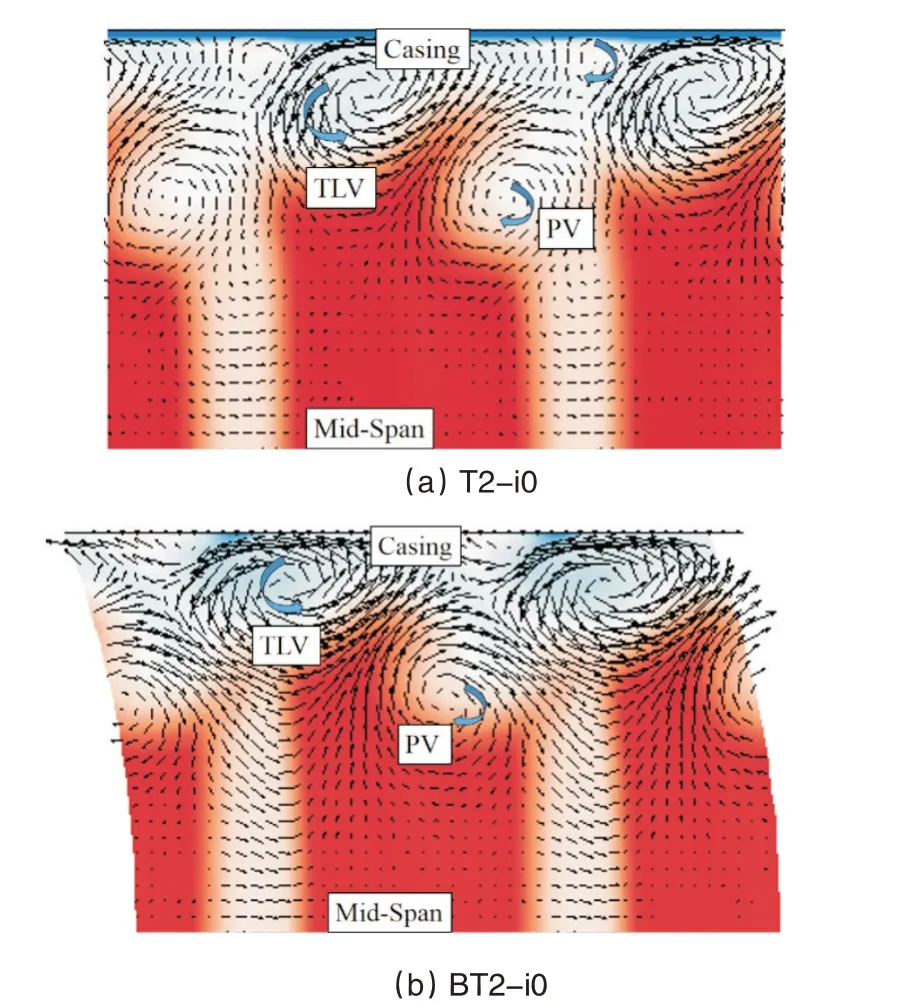
图26 叶栅尾缘下游50%轴向弦长处马赫数云图和二次流（2mm）Fig.26 Mach number contours and secondary flow vectors at 50%axial chord downstream of cascade trailing edge（2mm）

4.4 不同攻角下叶片弯曲对带叶尖间隙串列叶栅流场的影响

为了探究不同攻角下弯曲叶片对带叶尖间隙串列叶栅流场的影响，本节对叶尖间隙为2mm 的串列叶栅进行了研究，选取的攻角为0°（i0）、3°（i3）和5°攻角（i5）。由于0°攻角和3°攻角下弯曲叶片取得的效果相似，本节取0°攻角和5°攻角的工况进行研究。

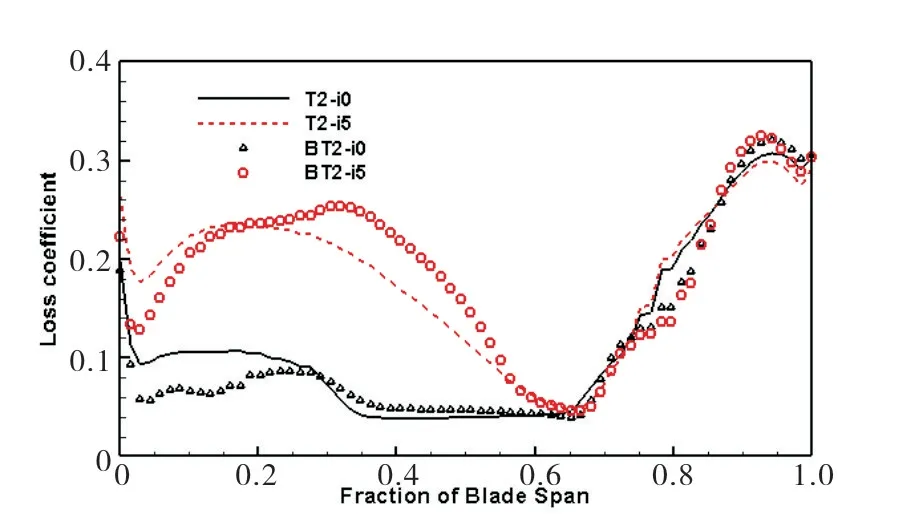
图27 叶栅尾缘下游50%轴向弦长处损失系数沿叶展分布Fig.27 Loss coefficient distribution along spanwise at 50%axial chord downstream of cascade trailing edge

由图27 可知，攻角越大，由于叶栅负荷增大，前排叶片有非常严重的角区失速，不同攻角下上端壁损失变化不大，攻角越大，下端壁损失越大。5°攻角下，叶片弯曲后，0到0.2叶展处的损失减小，0.2到0.6叶展处的损失增大，上端壁处损失不变，虽然在3°攻角下弯曲依旧能控制住角区分离，但5°攻角下，叶片弯曲虽然有一定的控制效果，已经不能完全控制角区失速。

图28展示了叶栅尾缘下游50%轴向弦长处的二次流和马赫数云图。攻角为5°时，叶栅上端壁由三个涡组成，靠近叶片压力面的是泄漏涡，靠近吸力面的是通道涡。通道涡是由通道中的低能流体和一部分叶尖泄漏流组成。在吸力面叶尖上端壁处有一个由泄漏涡诱导出来的涡。由马赫数云图可知，5°攻角下叶片弯曲不能控制泄漏流产生的损失。

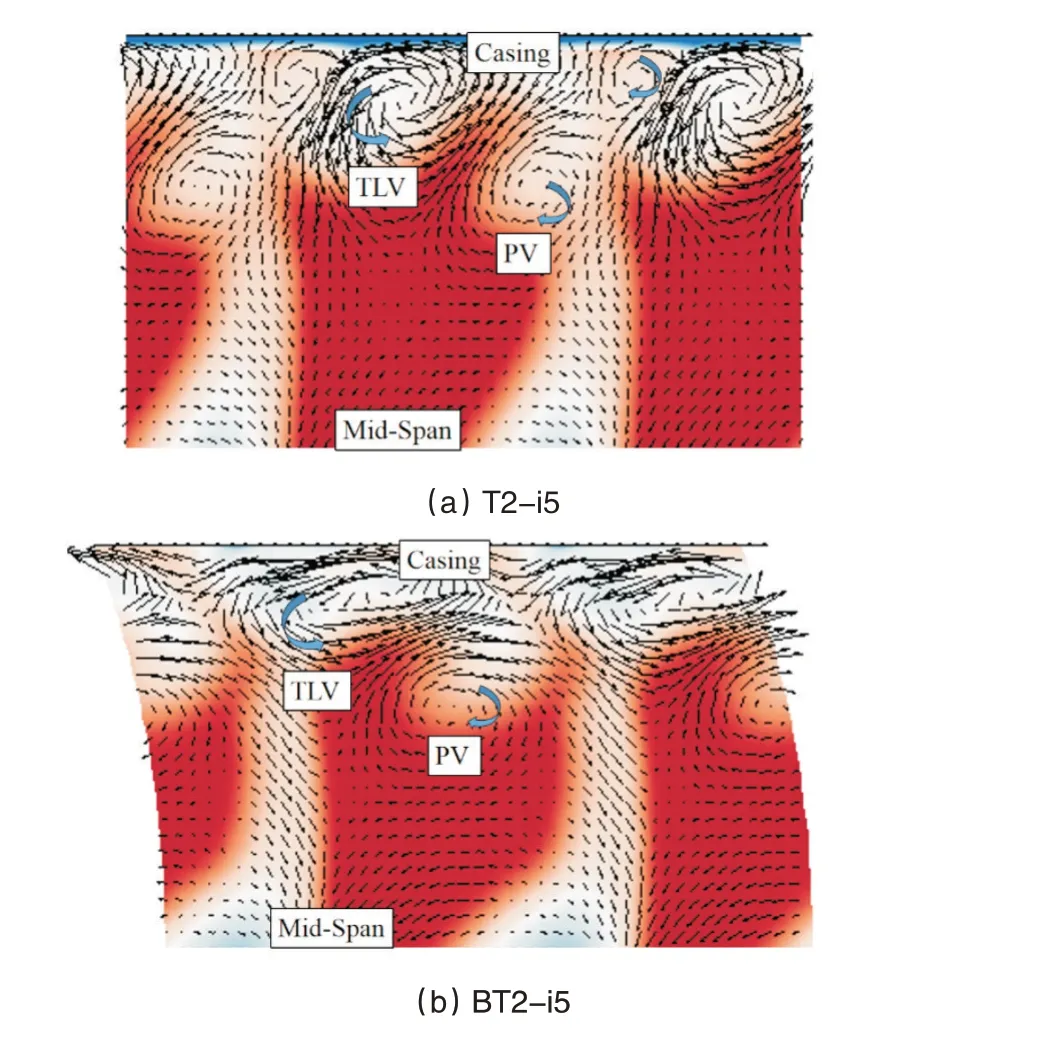
图28 叶栅尾缘下游50%轴向弦长处马赫数云图和二次流Fig.28 Mach number contours and secondary flow vectors at 50%axial chord downstream of cascade trailing edge

5 结论

1）叶片弯曲能有效控制高负荷串列叶栅中的角区失速，Bow20 工况使叶栅总损失最大降低了37.6%。叶片弯曲增大了端壁处的静压，减小了叶中的静压，且弯角越大，叶片沿叶展的压力梯度越大。采用弯曲叶片后，栅后平均马赫数降低，增大了串列叶栅的扩压能力。

2）串列叶栅只弯曲后排叶片的方案不能控制角区失速，且后弯曲叶片的采用恶化了叶栅的流场，使叶栅损失增大。前排叶片弯曲的方案取得的效果与两个叶片都弯曲取得的效果相似，但是叶栅损失略高于两个叶片都弯曲的方案，这是由于前排叶片弯曲使得后排叶片产生角区分离，而两个叶片都弯曲的方案将两部分角区失速都有控制作用。Bow20-A 工况使两个叶片叶中周向距离过大，前排叶片压力面的流体通过间隙流向后排叶片吸力面，使叶栅后部在叶中有两个尾迹区。Bow20-F工况由于相同的原因，在端壁角区有一个低速区中的高速区。

3）叶尖间隙能有效控制上端壁处的角区失速，且叶尖间隙越大，对角区失速的控制作用越大，叶栅损失降低得越多。叶尖间隙越大，泄漏涡的范围越大，且距离压力面越近。且叶尖间隙越大，上端壁区域的涡结构越复杂，2mm 工况下的通道涡由叶栅通道中的低能流体和一部分间隙流组成。弯曲叶片对下端壁的角区失速有控制作用，对叶尖间隙涡的控制作用不明显。

4）攻角越大，角区失速范围和损失越大，且攻角大于一定值时，叶片弯曲已经起不到对角区失速的控制作用,本文中3°攻角下叶片弯曲仍可以控制角区失速。且叶片弯曲对叶尖泄漏流的影响不明显。