一种基于间断Galerkin格式的新型限制器设计

郭永恒，杨 永，刘逸鸥

（西北工业大学 翼型叶栅空气动力学国防科技重点实验室，陕西西安 710072）

其中，¯H 代表单元交界面处的数值通量，它反映了当前单元和相邻单元之间的信息传递，这里采用 Roe格式对它进行处理。这样，整个离散系统就可以写成常微分方程的形式

一种基于间断Galerkin格式的新型限制器设计

郭永恒，杨 永，刘逸鸥

（西北工业大学 翼型叶栅空气动力学国防科技重点实验室，陕西西安 710072）

使用高阶间断 Galerkin格式求解守恒律方程组时，激波附近的 Gibbs效应容易导致非物理解的产生。为抑制这一现象，必须构造合理的限制器对数值解进行处理。目前间断 Galerkin格式中的限制器多源于有限体积法，在非结构网格上只对低阶导数项进行限制，对高阶导数项则很难给出普适判据。文章对间断 Galerkin解进行广义Fourier展开，实现不同频域范围内的谱分解；在新的模板坐标系下描述各阶方向导数的变化规律；结合当前单元和相邻单元的信息，分层限制各阶方向导数，实现对非物理解的抑制。通过求解Euler方程，对二维 Riemann问题、翼型周围的亚、跨声速流动问题、前台阶问题以及超燃冲压发动机内流场激波反射问题进行数值模拟，检验了新型限制器的可靠性以及向高阶格式推广的可行性。

间断 Galerkin格式；限制器；广义Fourier展开；模板坐标系；方向导数

0 引 言

航空航天事业的迅速发展，对计算流体力学提出了越来越高的要求，特别是在研究复杂流动问题方面，传统的有限体积法已经很难适应新形势的需要。于是，许多新型的高精度算法应运而生，其中，间断Galerkin格式［1］的研究与应用在最近几年逐渐成为一个热点问题，并在计算流体力学领域取得了一系列令人瞩目的结果。然而，当处理间断解问题时，Gibbs效应很容易导致非物理解的产生，使间断 Galerkin格式的计算过程出现中断。为了避免这种现象的发生，人们在间断Galerkin格式中应用大量的限制器，如Shu的斜率限制器［2］、Hoteit改进的 Van Leer限制器［3］、Tu和Aliabadi改进的Van Albada-typed限制器［4］、Qiu改进的WENO／HWENO 限制器［5］以及Krivodonova根据多元Taylor公式推导的限制器［6］。它们大多来源于传统的有限体积法，一般只对有限元解的低阶导数项进行处理，而对高阶导数项产生的非物理振荡抑制效果不佳甚至无法抑制，这使它们很难推广到高阶的空间离散格式中。从某种意义上说，限制器的设计已经成为制约高阶间断Galerkin格式应用的一个“瓶颈”。在这一背景下，本文结合间断Galerkin格式的具体形式，把握“局部解的方向导数”这一信息，并在新的模板坐标系下对其进行分层限制，有效避免了非物理解的产生，在保持高阶精度不变的同时，使计算过程得以顺利进行。

1 间断Galerkin格式的建立

直角坐标系下二维Euler方程的守恒形式为

首先，把整个求解区域Ω 划分成三角形非结构单元的集合，即其中 NE 为网格单元的个数；同时，在第k号单元上，设局部有限元解为

其中PHj是当前单元上的基函数，NP 为基函数的个数。根据加权余量法［7］的思想，令测试函数空间等于解函数空间，作如下内积，得

根据Gauss公式，可以得到间断Galerkin方程的弱守恒形式

其中，¯H 代表单元交界面处的数值通量，它反映了当前单元和相邻单元之间的信息传递，这里采用 Roe格式对它进行处理。这样，整个离散系统就可以写成常微分方程的形式

沿时间方向使用Runge-Kutta方法推进，就得到式（5）的数值解。

2 对问题单元的初筛

在式（2）中，依 Gram-Schmidt过程［8］构造规范正交基，并通过线性变换，把每个物理单元映射成计算域

对应的基函数的具体表达式为当选取前6个基函数时，对应的空间离散精度为三阶。从广义Fourier级数的角度来看，正交基函数连同前面的系数QHj构成了有限元解的低频分量和高频分量，这是新型限制器设计的出发点。按照Gibbs效应［9］的相关理论，非物理振荡对应的广义 Fourier系数QHj不能快速的衰减。 对于三阶格式，在此约定，把有限元系数分为三层，即平均层｛QH1｝、一次层｛QH2，QH3｝和二 次层｛QH4，QH5，QH6｝，它 们 对应 于 守恒变量的积分平均值、一阶和二阶空间导数分量。接着，定义无量纲的振荡参数

这里，把β1和β2称为一次、二次相对振荡强度。首先判断一次层，当β1大于一定的控制阀值μ1时，需要对一次层进行限制；然后判断二次层，当β2大于一定的控制阀值μ2时，需要对二次层进行限制。在实践过程中，我们选取密度项对应的广义Fourier系数对β1和β2进行计算。这样，我们就完成了对问题单元的初筛。在这个阶段，控制阀值越小，初筛越敏感，在接下来的限制过程中判断是否需要进行重构的计算量越大。在实践过程中，当这些参数处于同一量级（μ1为10-2量级，μ2为10-4量级）时，计算结果几乎是一致的。也就是说，计算精度主要不是由问题单元的初步筛查来单独决定的，而是结合接下来的限制过程决定的。

3 模板坐标系下的限制器设计

非结构网格单元排列无序且缺乏正交性。如果单纯采用计算坐标系ξ-o2-η，就很难反映当前单元和相邻单元之间的空间联系；如果单纯采用物理坐标系x-o1-y，就很难像结构网格那样对信息传递的方向进行很好的判断。这里，我们建立模板坐标系，并结合方向导数的相关信息构造新型限制器。如图1所示，记当前单元和相邻单元的重心分别为G0、G1、G2、G3，相应的三个模板依次为（0，1，2）、（0，2，3）、（0，3，1），特别的，对于边界处的单元，只存在一个模板。

物流企业不同于其他的制造性企业，其发生的成本费用没有专门的会计制度来规范。在进行成本核算过程中，各企业往往按照现行的《企业会计制度》来核算。但是物流企业提供的服务时无形的，其成本核算对象不易选取，在核算方面必然存在缺陷，管理层也无法得到最精确的成本数据，无法达到管理的目的。在账务核算时，没有专门的会计科目来进行归集和分类，不易对某一环节发生的费用进行控制。一般来说，企业根据财务的会计科目来做成本预算，这样不利于物流企业对成本进行控制。大部分物流企业采用传统成本法下的科目来核算，如将不同环节发生的物流成本统一归集到“管理费用”等期间费用中，无法核算各个作业下的成本信息。

图1 模板坐标系示意图Fig.1 A diagram for the mode coordinate system

以第1号模板为例，令当前单元的重心 G0为原点o3，分别连接该点与1、2号单元的重心 G1、G2，构成两个线性无关的方向r和s，于是，新的模板坐标系即定义为r-O3-S。对于一次层，我们分析其一阶方向导数在当前单元上可以通过复合函数的链导法则 进 行计 算；另 一方 面的数值也可以通过有限差分法直接进 行 计算，其 表 达 式为和 Q（2）H 1分 别 为 第 1、2 号 单 元的第一项广义Fourier系数，r01和s02分别为当前单元重心G0和第1、2号单元重心G1、G2之间的距离。设修正后的一次层系数为那么

这样，联立式（9）、（10）就可以求出修正后的一次层系数。对于模板1，我们定义一个加权因子w1=β1（3），即第3号单元的一次相对振荡强度。可以看出，当第3号单元上的振荡相对较强时，这样的定义方式模板1中重构的信息所占的加权比重相对更大一些。同理，可定 义于是最后的加权修正结果

为

类似的，我们可以进一步比较高阶方向导数的解析结果和差分结果，建立如下三个限制方程

联立方程（13）、（14）、（15）就可以求出修正后的二次层系数，对于模板1，我们定义一个加权因子w1为w1=β（3）

2，即第3号单元的二次相对振荡强度。

就这样，我们通过对不同阶次的方向导数的逐层分析，最终完成了对广义Fourier系数的限制。可以证明，一方面，当略去高阶项的限制部分后，本文的限制器形式非常接近于Shu的斜率限制器［2］，所以该限制器可以视为Shu限制器向更高阶格式的推广；另一方面，当问题退化到一维情况或者结构化网格情况时，方向导数可以用偏导数直接代替，这又和Krivodonova设计的限制器［6］非常相似，只是后者从高阶部分向低阶部分依次进行限制，本文的限制器的处理次序与之相反，所以它又可以视为Krivodonova限制器向非结构网格的推广。很显然，这种分层限制的处理方式可以方便的推广到更高阶的格式中。

4 数值算例分析

为了检验新型限制器在光滑解附近对精度的影响，首先计算NACA0012翼型的亚声速流场问题，设定计算状态为：Ma∞=0.63，α=2°，对应的物面压强系数分布曲线和等压线分布如图2、3所示。在不使用限制器的条件下，这个算例依然能够得到收敛的光滑解。从图2中可以看出，加入分层限制器后，压强系数分布基本没有发生变化；从图3中可以看出，使用限制器后，等压线仍然是很光滑的。所以，可以认为分层限制器有利于光滑解区域高精度的保持。

图2 NACA0012翼型压强系数分布（亚声速）Fig.2 The distribution of pressure coefficient for NACA0012（subsonic）

图3 NACA0012翼型等压线分布（亚声速）Fig.3 Lines of constant pressure for NACA0012（subsonic）

为了验证新型限制器在捕捉激波时的有效性，本文计算了两个二维Riemann问题［10］，它的物理背景为：把［0，1］×［0，1］区域等分为四个彼此隔离的正方形子区域，每个区域上设定一个初始的流动状态，然后撤掉隔板，研究整个区域的流场变化规律。初始时刻算例1和算例2的密度ρ、速度u、v和压强p的空间分布以及输出流场数据时的计算时刻t见表1。相应时刻密度ρ的分布情况如图4、5所示。在新型限制器的辅助下，高阶间断Galerkin格式所计算出的激波位置以及形状和文献［10］的结果吻合得很好，激波干涉的细致结构得以生动的体现。

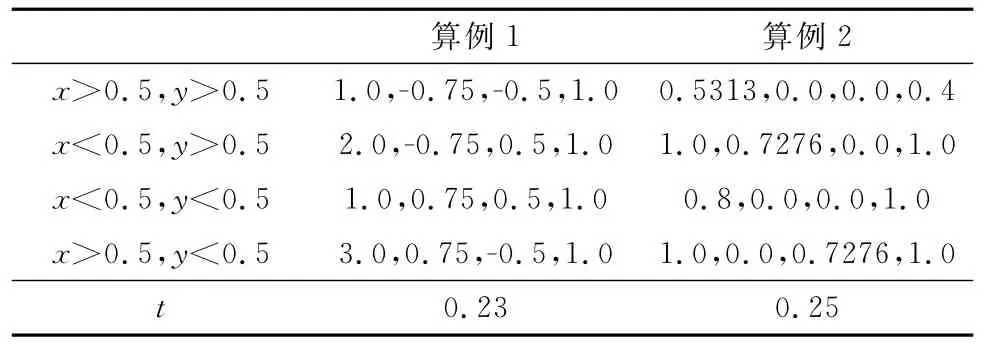
表1 二维Riemann问题初始状态（ρ，u，v，p）及计算时刻tTable 1 Initial state（ρ，u，v，p）and final time for the 2D Riemann problem

接着，计算NACA0012和RAE2822翼型的跨声速流场，无穷远处自由来流状态分别为Ma∞=0.8，α=1.25°和Ma∞=0.729，α=2.31°，对应的物面压强系数分布曲线和等压线分布如图6～图9所示，其中也给出了利用Shu限制器和HWENO限制器得到的对比曲线。可以发现，相对于Shu限制器，本文的限制器在激波附近更好的抑制了非物理振荡；相对于HWENO限制器来说，本文的限制器对激波的识别更加敏感，对应的曲线间断部分更加陡峭。

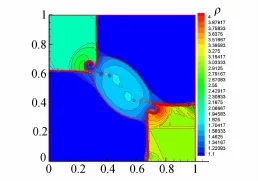
图4 二维Riemann问题密度等值线，t=0.23（算例1）Fig.4 Lines of constant density for 2D Riemann problem，t=0.23（case 1）

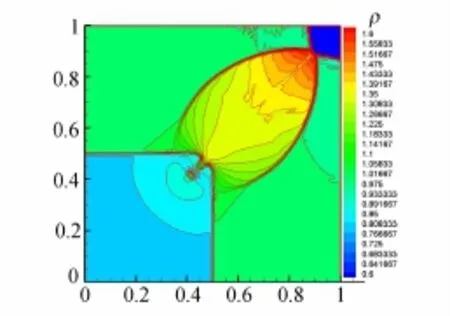
图5 二维Riemann问题密度等值线，t=0.25（算例2）Fig.5 Lines of constant density for 2D Riemann problem，t=0.25（case 2）

图6 NACA0012翼型压强系数分布（跨声速）Fig.6 The distribution of pressure coefficient for NACA0012（transonic）

图7 NACA0012翼型等压线分布（跨声速）Fig.7 Lines of constant pressure for NACA0012（transonic）

图8 RAE2822翼型压强系数分布（跨声速）Fig.8 The distribution of pressure coefficient for RAE2822（transonic）

图9 RAE2822翼型等压线分布（跨声速）Fig.9 Lines of constant pressure for RAE2822（transonic）

然后，我们计算了一个前台阶问题，这是一个比较难于计算的非稳态测试模型，因为台阶角点会产生压力奇性。相关几何模型的数据详见文献［11］，计算区域上三角形单元数为17000，节点数为8751，超声速入口条件为Ma∞=3，α=0°，计算时刻为t=4，其密度等值线和压强等值线如图10、11所示。与文献［11］的结果相比较，可以发现，结合新型限制器的间断Galerkin格式能够很精确的计算出激波的反射位置和反射角。

图10 前台阶问题密度等值线分布（t=4）Fig.10 Lines of constant density for the flow in the wind-tunnel with a front step（t=4）

图11 前台阶问题压强等值线分布（t=4）Fig.11 Lines of constant pressure for the flow in the wind-tunnel with a front step（t=4）

最后，我们计算一个超燃冲压发动机的内部流场，这是一个定常问题，相关几何模型数据详见文献［12］，计算区域上三角形单元数为12828，节点数为6785，超声速入口条件为Ma∞=3，α=0°，出口处采用超声速边界条件，稳定状态下的密度等值线和压强等值线如图12、13所示。与文献［12］的计算结果相比，可以发现，在新型限制器的帮助下，间断Galerkin格式处理复杂流动问题的能力得到了进一步的展示。

图12 超燃冲压发动机密度等值线分布Fig.12 Lines of constant density for the flow in the scramjet engines

图13 超燃冲压发动机压强等值线分布Fig.13 Lines of constant pressure for the flow in the scramjet engines

5 小结与展望

本文建立了模板坐标系，沟通了非结构网格单元与相邻单元的联系。进一步的，在分析Gibbs现象的数值特征的基础上，对各阶方向导数进行了分层限制，从而对各阶广义Fourier系数进行了重构。大量的数值结果表明，本文设计的新型限制器能够有效的抑制间断解附近产生的非物理振荡，从而使计算过程得以顺利进行，同时，它保持了间断Galerkin格式高精度逼近的优越性，为其在工程中的广泛应用打下了坚实的基础。今后，可以在本文的基础上，对 Gibbs现象初筛部分做更加深入的研究并提出新的判据，在限制器构造部分研究更高精度的差分格式，对加权平均因子进行新的改进，从而进一步提高间断Galerkin格式处理复杂流动问题的能力。

［1］ REED W H，HILL T R.Triangular mesh methods for the neutron transport equation［R］.Technical Report LA-UR-73-479，Los Alamos Scientific Laboratory，1973.

［2］ COCKBURN B，SHU C W.The Runge-Kutta discontinuous Galerkin method for conservation laws v：multidimensional systems［J］.J Comput Phys，1998，141：199-224.

［3］ HOTEIT H，ACKERER P，MOSE R，et al.New two-dimensional slope limiters for discontinuous Galerkin methods on arbitrary meshes［R］.Institut National de Recherche en Informatique et en Automatique（France），Rapport de Recherche，n 4491，July 2002.

［4］ TU S，ALIABADI S.A slope limiting procedure in discontinuous Galerkin finite element method for gasdynamics applications ［J］.Int.J.Numer.Anal.Model.，2005，2（2）：163-178.

［5］ QIU J，SHU CW.A Comparison of trouble cell indicators for Runge-Kutta discontinuous Galerkin methods using WENO limiters［J］.SIAM Journal on Scientific Computing，2005，27 （3）：995-1013.

［6］ LILIA KRIVODONOVA.Limiters for high-order discontinuous Galerkin methods［J］.Journal of Computational Physics，2007，226：879-896.

［7］ WANG L H，Xu X J.The mathematical foundations of the finite element method［M］.Beijing：Science Press，2004.（in Chinese）王烈衡，许学军.有限元方法的数学基础［M］.北京：科学出版社，2004.

［8］ CHENG Q X，ZHANG D Z，WEI G Q.Real variable function and functional analysis［M］.Beijing：Higher Education Press，2003.（in Chinese）程其襄，张奠宙，魏国强.实变函数与泛函分析［M］.北京：高等教育出版社，2003.

［9］ JAN S HESTHAVEN，TIM WARBURTON.Nodal discontinuous Galerkin methods：algorithms，analysis，and applications ［M］.Springer，2008：135-145

［10］KURGANOV A，TADMOR E.Solution of two-dimensional Riemann problems for gas dynamics without Riemann problem solvers［J］.Numerical Methods Partial Differential Equations，2002，18：584-608

［11］WOODWARDP，COLELLA P.The numerical simulation of two-dimensional fluid flows with strong shocks［J］.J.Comput. Phys.，1984，54：115-173

［12］SHUANGZHANG Tu，SHAHROUZ ALIABADI.A slope limiting procedure in discontinuous Galerkin finite element method for gas dynamics applications［J］.International Journal of Numerical Analysis and Modeling，2005，2（2）：163-178.

An original designed limiter for discontinuous Galerkin method

GUO Yongheng，YANG Yong，LIU Yiou

（National Key Laboratory of Science and Technology on Aerodynamic Design and Research，Northwestern Polytechnical University，Xi′an 710072，China）

When the high-order discretization scheme is applied for solving the hyperbolic conservation laws，the Gibbs oscillations emerging around the discontinuities may cause the fields to take unphysical values，which could result in the undesired interruption of calculation process.This problem is especially severe for the discontinuous Galerkin scheme.Therefore，suitable limiting calculators are supposed to be designed in order to damp the appearance of unphysical oscillations.However，the existed limiters for the discontinuous Galerkin scheme originate mostly from the finite volume methods，thus for the unstructured grids they can only limit the spatial solutions of the solutions，namely the lower-order derivatives，rather than offer an general criterion for the higher order derivatives.Due to this background，the discontinuous finite element solutions are firstly processed into general Fourier expansion series for the realization of spectral decomposition in different frequency domains.Afterwards，a modal coordinate system is originally proposed，describing the changing patterns of the directional derivatives in different orders in a new form.Finally，after the combination of the information of the current mode and its adjacent mode，and the limitation of the directional derivatives in different orders for different levels，the unphysical solutions are successfully damped.Based on this method，the Euler equations are solved for the numerical simulations of the 2-D Riemann problems，the flow field of the wind-tunnel with a front step，the reflection of shockwaves in the inner field of scramjet engines as well as the subsonic and transonic flow surrounding airfoils.The obtained results demonstrate that the new limiter is relatively reliable and it can be generalized to high-order schemes.

discontinuous Galerkin scheme；limiting calculators；general Fourier expansion；mode coordinate system；directional derivatives.

V211.3

Adoi：10.7638／kqdlxxb-2012.0157

0258-1825（2014）04-0462-06

2012-10-16；

2013-03-05

郭永恒（1982-），男，西北工业大学博士研究生，主要从事理论与计算流体力学的研究.

郭永恒，杨永，刘逸鸥.一种基于间断Galerkin格式的新型限制器设计［J］.空气动力学学报，2014，32（4）：462-467.

10.7638／kqdlxxb-2012.0157. GUO Y H，YANG Y，LIU Y O.An original designed limiter for discontinuous Galerkin method ［J］.ACTA Aerodynamica Sinica，2014，32（4）：462-467.