翼型模型几何误差对气动性能影响的自动微分分析方法
2014-09-12徐林程叶正寅
徐林程,王 刚,武 洁,叶正寅
(西北工业大学,翼型、叶栅空气动力学国防科技重点实验室,陕西 西安 710072)
其中:
翼型模型几何误差对气动性能影响的自动微分分析方法
徐林程,王 刚,武 洁,叶正寅
(西北工业大学,翼型、叶栅空气动力学国防科技重点实验室,陕西 西安 710072)
基于自动微分原理和 NS方程有限体积方法建立了一套翼型敏感性导数计算方法和程序,可以一次性获得翼型不同气动力系数、压力分布对模型几何外形误差的敏感性导数和不确定度。计算结果表明,在跨声速范围内,即使翼型的外形误差只有63μm(弦长1m),也可以给翼型压力分布带来0.312(以来流动压为参考)量级的不确定度,而激波处的流动最为敏感。这种自动微分方法对于分析数值模拟结果的分散性、风洞试验结果的分散性或不确定性具有很好的指导意义。
几何误差;不确定性;敏感性分析;自动微分;跨声速;翼型
0 引 言
气动外形决定了飞行器的气动性能,无论是数值计算还是风洞试验,人们一直致力于提升对某个外形气动性能的预测精度。从风洞试验角度,外形加工误差、模型结构本身变形(可以是因为载荷作用、也可以是因为气候变化带来的物理变形)都会引起外形的变化;从数值计算角度讲,几何外形的连续曲线会被离散为折线段,网格划分策略和网格数量就决定了计算外形与实际外形的差别,而且在网格生成过程中,插值运算本身也会在某种程度上引起几何误差,这些外形的改变到底会给气动性能的预测带来多大的影响?这是一个有实际意义的基本问题,虽然问题“显而易见”,但长期以来没有一个定量的分析方法研究该问题。解决这个问题的方案可以从国外近年来采用的不确定性分析途径进行分析[1-7]。在不确定性分析过程中,最重要的技术环境就是获得不同的敏感性导数,对于导数的求解方法,最直接的方式就是利用差商法获取,随着CFD技术的发展和成熟,利用CFD工具计算这些敏感性导数理论上是可以实现的,但是,对于众多的敏感性导数,如果采用简单的差分算法意味着巨大的计算量。而且,对于几何外形很小的变化,要准确地计算出他们之间的气动性能差异,对计算方法和软件是一个很大的挑战。此外,CFD软件计算的结果还受到网格数量、收敛精度等因素的影响,而差分算法中步长的选取也对敏感性导数值产生影响。为了更有效地获得敏感性导数,国外引入自动微分 方法[8-11],这种 方 法直 接 伴随 CFD 方 法 求解 空气动力学基本方程的实际流程,敏感性导数的计算也是数学意义上严格的微分概念,更有价值的是,只要开发出的计算程序设计合适,可以一次性同时获得大量的敏感性导数,而且敏感性导数的收敛精度与流场的收敛精度达到相同的量级,为不确定性分析开辟了一条新的技术途径。
本文以跨声速翼型为对象,在课题组CFD程序基础上,应用自动微分工具 Tapenade对程序进行改造,对典型超临界翼型的几何敏感性导数进行计算,给出压力系数分布对各处几何外形的不确定性分析。这项工作对于认识数值计算和风洞试验中外形参数变化引起的性能预测误差有重要的实际意义。
1 自动微分方法
自动微分是面向计算程序,应用求导的链式法则,求取程序输出量对输入量偏导数的一种方法。任何计算程序是由有限个赋值序列组成,即
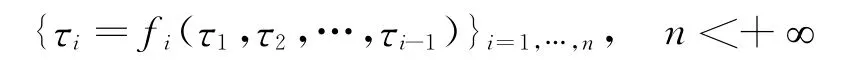
而编译器会将所有的数值运算分解为计算机硬件能够执行的加,减,乘,除四则基本运算,由于四则基本运算在数学上都是显式析可微且可导的,因此所有计算机程序能表达的数学运算,理论上是至少单侧可微的,即偏导数
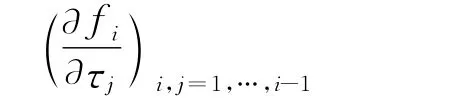
都解析存在,并且可以显示表达。令

其中D为求导算子,D f为程序中赋值语句基于自身数学结构对所有变量求导,Dτ为变量基于程序全局数量关系对所有变量求导,展开后得可得:

对Dτ的每一项应用链式法则:

表示为矩阵形式,即为

对上式两端同时进行转置运算,可得

其中I为单位矩阵。
方程(1)给出了自动微分前向求导模式的求解顺序和算法

方程(2)给出了自动微分逆向求导模式的求解顺序和算法

由于上述推导过程没有引入数学或物理假设,不包含除法运算,并且每个环节都是严格精确的解析过程,因此,自动微分求导过程结果没有截断误差,精度与原程序相同。对于线性问题,自动微分过程的收敛速度,稳定性与原程序一致[13]。此外,单目标函数的逆向自动微分过程计算量最多不超过原程序计算量的5倍已得到理论上的证明[15]。
2 空气动力学计算方法
本文以跨声速马赫数范围的二维超临界翼型问题为研究对象,以课题组非结构网格求解雷诺平均N-S方程的计算程序为基础,应用Tapenade[15]软件进行自动微分方法的进一步改造。原程序以雷诺平均的可压缩、非定常N-S方程为流动基本方程,采用目前认为通用性较好的SA湍流模型,应用有限体积法对空气动力学基本方程进行离散求解[12],并且运用了当地时间步长、隐式时间推进等加速收敛措施。
流动基本方程的积分形式为:

其中:

ρ、u、v、e分别为空气密度,x、y方向的速度分量和单位体积的总内能,n为线积分的法向单位向量,V 为积分域,∂V 为积分域的边界,F为通量项,它包括无粘项FE和粘性项Fv,V 为速度矢量,i、j分别为x、y方向的单位矢量,τ为粘性应力。

图1 翼型附近的非结构混合网格Fig.1 Unstructured hybrid mesh attached to the airfoil

图2 第一层网格格心的y+分布Fig.2 Distribution of y+value of the first grid layer
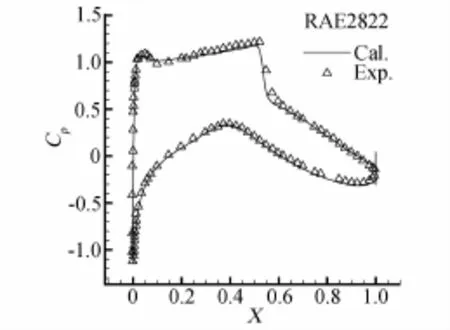
图3 翼型的压力系数分布Fig.3 Pressure coeffecients distribution of the airfoil

图4 计算过程的残值收敛历程Fig.4 Convergence course of computing process
图1~图4是在迎角α=2.31°,马赫数 Ma= 0.729,雷诺数Re=650万的状态下,原程序计算超临界翼型RAE2822跨声速流场的网格和结果。为了模拟附面层流动,在翼型壁面附近采用了层状的网格结构,第一层网格高度为4.0e-6。可以看出,原CFD程序具有良好的收敛特性,同时计算结果与实验数据[16]吻合程度高,物面Y+值都小于1.2,因此网格是比较合理的,并且原CFD程序具有较好的计算精度。
3 计算结果分析
为了验证在空气动力学方程求解程序基础上改造的自动微分程序,首先通过传统的差分方法计算出翼型前缘附近某点的压力系数对该点坐标变量的敏感性导数,然后采用改造后的自动微分程序对该敏感性导数进行计算。其结果如表1所示,可以看出,采用自动微分的方法与采用传统差分方法的计算结果接近。此外,压力系数对x坐标的敏感性要大于对y坐标敏感性导数一个量级。

表1 不同方式计算的对翼型前缘坐标的敏感性导数Table 1 Derivatives of surface pressure coefficient with respect to local coordinates from different differentiation methods
其中,In V 为自变量(Independent Variables),Var为变量(Variables),DS为差分步长(Difference Step),FD为前向差分(Forward Difference),AD为自动微分(Automatic Differentiation)。
在上述方法验证的基础上,以翼型表面坐标值为输入变量,以翼型表面的压力系数为输出变量,由Tapenade软件对源程序生成自动微分前向求导程序,进行计算。
图5显示了翼型表面各点压力系数对物面各点坐标偏导数的总体分布,(a)图针对x坐标,(b)图针对y坐标。图6是图5两图对应的沿x方向视图,图中每条曲线描述的是翼型表面某一点的Cp对各点坐标的敏感程度,图中的曲线族在横轴某区间的聚集程度和幅值大小,表征着该区间坐标对物面各处压力系数的总体影响能力。图7是图5两图对应的沿y方向视图,图中每条曲线描述的是翼型表面某一点的坐标对各点压力系数的影响能力,图中曲线族在横轴某区间的聚集程度和幅值大小,表征着该区域压力系数对物面坐标的总体敏感性。

图5 Cp对物面坐标导数的整体分布Fig.5 Derivatives of pressure coeffecients with respect to surface coordinates
可以看到,图5(a、b)两图具有一些相似的基本特征。首先,偏导数总体量级很小,但在沿着XY平面内的对角线上有明显的突起,这说明每个点坐标主要对当地或者相近点附近的流场有明显影响。其次,偏导数在激波位置存在明显的带状突起,在翼型前缘和后缘有尖锐的峰值,结合图6,可以看到,在x=0附近的前缘附近,x=1.0的后缘附近和有激波存在的0.5<x<0.6区域内,曲线高密度聚集,并且存在幅值峰,可见,这三个区域的物面坐标对流场有很强的影响能力;结合图7,可以看到,在x=0的前缘附近和x=1.0的后缘附近和有激波存在的0.5<x<0.6区域内,曲线高密度聚集,并且存在幅值峰,可见,这三个区域的流场对物面扰动的感知能力很强。此外,在翼型中后段,图5(b)图在对角线上的突起要比图5(a)强很多,这主要是因为该部分的物面法向与y′坐标方向接近。
为了进一步量化几何误差对翼型压力分布的影响,考虑到采用7级精度加工弦长一米的翼型模型,表面公差会达到63μm,利用已获得的x、y方向的偏导数合成各物面点垂直物面方向的偏导数,取物面在法向的摄动为63μm,则压力分布的不确定度如图8所示,其中,图8(a)是翼型压力系数不确定性分布的单独显示,图8(b)是翼型压力系数不确定性附着在压力系数上的显示。

图6 物面坐标影响曲线云图Fig.6 Effect curves of surface coordinates to pressure coeffecients
对照图8中的 (a)、(b)两图,不难发现翼型上表面压力分布的不确定度在前缘和激波位置出现峰值,并且在激波处取得最大值0.312,显然,在这两个位置之间的超声速区域,压力系数不确定度明显高于其余的亚声速区域,这说明,翼型在跨声速流中,超声速区比亚声速区要对物面坐标敏感。

图7 Cp敏感性曲线云图Fig.7 Sensitivity curves of pressure coeffecients with respect to surface coordinates

图8 物面坐标不确定度诱导的压力分布不确定度Fig.8 Uncertainties of surface pressure coeffecients caused by surface coordinates perturbations
图8(a)表明,在物面63μm 的摄动下,压力系数的不确定度会达到0.312(以来流动压为参考)的量级,可以从翼型模型加工和数值模拟两个角度看待这个结果。
从翼型模型加工的角度看,要获得更高精度的风洞试验结果,必须采用更高精度的加工方法制作翼型模型。此外,由于不同区域物面坐标对流场的影响能力相差悬殊,在加工翼型模型过程中,对敏感区域(需要预先进行几何外形的敏感性分析),例如:翼型前缘,激波位置(需要预先估测)等,进行特殊处理,单独提高其加工精度,将对提高风洞试验结果的精度取得事半功倍的效果。
从数值模拟的角度看,由于物面总是被离散成有限个点,用折线代替曲线,如图9所示,显然,这个过程会引起外形误差。根据几何关系可得:

其中,δ、ρ、Δl分别表示外形误差,当地曲率半径,网格长度。令ε为计算结果所需要达到的精度,χ 为流场对物面几何误差的敏感程度(这里为物面压力系数对物面几何误差敏感性的最大值,即0.312×106/63 ≈5000),则当地网格长度应满足如下关系定量关系:

上式是从敏感性角度出发,得到的当地网格长度最大值的表达式,以下简称为物面网格密度的敏感性准则。可见,CFD数值模拟要获得指定精度的结果,物面网格密度必须满足式(6)才是可能的。

图9 曲线的离散公差Fig.9 Geometry error of curves caused by dicretisation
4 结 论
采用有限体积法求解雷诺平均 Navier-Stokes方程的程序为基础,运用自动微分方法建立了一套翼型敏感性导数计算方法和程序,在此基础上,研究了在跨声速流场中模型几何误差对翼型表面压力分布的影响。研究表明,在跨声速范围内:
物面坐标主要影响当地的流场,但是,激波附近的物面坐标会显著影响物面各处的流场,同时,激波位置的流场能够明显感受到物面各处坐标的存在,并且,在翼型前缘区域和后缘区域,物面坐标对流场的影响能力和流场对物面坐标的敏感性都很强。
7级精度的加工误差,在本文所取的来流状态下,会给翼型表面压力系数分布带来0.312(以来流动压为参考)量级的不确定度。降低加工误差对风洞试验结果的影响需要更高精度的加工手段。数值模拟中,物面网格密度满足敏感性准则(详见式(6)),计算结果达到预期精度才能有实际物理意义。同时,翼型上表面的超声速区域流场明显比翼型表面亚声速区域流场对几何误差更敏感,并且翼型前缘和激波位置会出现敏感性尖峰,这从一个方面解释了为什么在风洞试验和数值模拟中,上表面压力分布分散性比下表面大;翼型吸力峰值附近和激波附近的压力系数分散性大。
[1] WEAVER A B,ALEXEENKO A A,et al.Flow field uncertainty analysis for hypersonic CFD simulations[R].AIAA Paper 2010-1180.
[2] BETTIS B R,HOSDER S.Uncertainty quantification in hypersonic reentry flows due to aleatory and epistemic uncertainties [R].AIAA Paper 2011-0252.
[3] DEEPAK BOSE D,BROWN J L,et al.Uncertainty assessment of hypersonic aerothermodynamics prediction capability [J].Journal of Spacecraft and Rockets,2013,50(1):12-18.
[4] KUCHI-ISHI S.Uncertainty evaluation of thermocouple aeroheating measurements for hypersonic wind-tunnel tests[J].Journal of Spacecraft and Rockets,2006,43(3):698-700.
[5] KAMMEYER M E,RUEGER M L.On the classification of errors:systematic,random,and replication level[R].AIAA Paper 2000-2203
[6] ULBRICH N.Test data uncertainty analysis algorithm of NASA Ames wind tunnels[J].AIAA Journal,2003,41(8):1616-1619.
[7] KAMMEYER M E,WOZNIAK R W.An uncertainty analysis for low-speed wind tunnel pressure measurements[R].AIAA Paper 2004-2196.
[8] MADER C A,MARTINS J R R A.Computation of aircraft stability derivatives using an automatic differentiation adjoint approach[J].AIAA Journal,2011,49(12):2737-2750.
[9] JONES D,MUELLER J D,BAYYUK S.CFD development with automatic differentiation[R].AIAA Paper 2012-0573.
[10]ZHOUJIE LYU Z,GAETAN K W,KENWAY G K W,et al.Automatic differentiation adjoint of the reynolds-averaged Navier-Stokes equations with a turbulence model[R].AIAA Paper 2013-2581.
[11]DALLE D J,DRISCOLL J F.Continuous differentiation of complex systems applied to a hypersonic vehicle[R].AIAA Paper 2012-4958.
[12]JIANG Y W,YE Z Y,WANG G.Efficient solution of Euler/N-S equations on unstructrured grids[J].Chinese Journal of Computional Mechanics,2012,29(2):217-233.(in Chinese)蒋跃文,叶正寅,王刚.基于非结构网格的高效求解方法研究[J].计算力学学报,2012,29(2):217-223.
[13]GILES M B,GHATE D,DUTA M C.Using automatic differentiation for adjoint CFD code development[R].Oxford:Oxford University Computing Laboratory.2005.
[14]GRIEWANK A.On automatic differentiation.in:mathematical programming’88[M].Kluwer Academic Publishers,Dordrecht,1989.
[15]HASCOЁT L,PASCUAL V.TAPENADE 2.1 user’s guide [R].INRIA,Sophia-Anpipolis,2004
[16]THIBERT J J,GRANJACQUES M,OHMAN L H.RAE2822 airfoil agard advisory report No.138[R].Experimental Data Base for Computer Program Assessment,1979,A182.
An automatic differentiation method for uncertainty analysis due to airfoil configuration variation
XU Lincheng,WANG Gang,WU Jie,YE Zhengyin
(National Key Laboratory of Aerodynamic Design and Research,NWPU,Xi’an 710072,China)
Focused on the quantification of the uncertainties of areodynamics performance of airfoils with respect to geometry error,with a set of CFD program based on finite volume algorithm solving the Reynolds-Averaged Navier-Stokes equations with S-A turbulent model,adopting automatic differentiation method to reform the program simultaniously,all kinds of sensitive derivatives,uncertainties of all kinds of aerodynamic coefficients and pressure coefficients distribution resulting from geometry error could be obtained in one course of computation.As the computational results show,even if the geometry error is only 63 microns (while the length of chord is 1 meter),the pressure distribution of the walls could be influenced obviously with uncertainty quantity reaching 0.312(taking dynamic pressure of the flow as reference)for an airfois in transonic flow,moreover,pressure attached to the place where shock wave stationed bears peak uncertainty.the results of method of automatic differentiation account for the dispersity of results of numeric simulations and wind tunnel experiments well.
geometry error;uncertainty;sensitivity analysis;automatic differentiation;transonic flow;airfoils
V211.3
Adoi:10.7638/kqdlxxb-2013.0097
0258-1825(2014)04-0551-06
2013-10-15;
2014-01-02
国家自然科学基金(11272264)
徐林程(1989-),男,研究生,研究方向:理论与计算流体力学.E-mail:993644844@qq.com
徐林程,王 刚,武 洁,等.翼型模型几何误差对气动性能影响的自动微分分析方法[J].空气动力学学报,2014,32(4):551-556.
10.7638/kqdlxxb-2013.0097. XU L C,WANG G,WU J,et al.An automatic differentiation method for uncertainty analysis due to airfoil configuration variation[J].ACTA Aerodynamica Sinica,2014,32(4):551-556.
