考虑波浪形底面影响的边界层风场大涡模拟
2014-09-12孙丽明曹曙阳张恩臻
孙丽明,曹曙阳,李 明,杨 青,张恩臻
(同济大学 桥梁工程系土木工程防灾减灾国家重点实验室,上海 200092)
考虑波浪形底面影响的边界层风场大涡模拟
孙丽明,曹曙阳,李 明,杨 青,张恩臻
(同济大学 桥梁工程系土木工程防灾减灾国家重点实验室,上海 200092)
为了研究强风作用下海面上的平均风剖面,采用大涡模拟方法对带有余弦波形状底面、自由滑移顶面的渠道流进行了模拟,波幅、波高比2a/λ为0.1,基于平均速度Ub和渠道高度的雷诺数Reb为6760。统计结果表明,波浪形下表面对上方风场分布有着显著的影响,y/H=0.3(y+≈200)是内区、外区的分界线,内区受壁面影响显著,外区受壁面影响较小。流动的分离点位于x/λ=0.14,而再附点位于x/λ=0.65。展向速度脉动峰值出现在上坡处,且超过竖向脉动。表面压力要比表面摩擦力大一个数量级,是阻力的主要来源。随着波幅的增大,回流区面积增大,速度峰值和展向脉动峰值也会增大,展向脉动峰值甚至会超过流向脉动峰值。
大涡模拟;波浪形渠道流;平均风剖面;渠道流;摩擦阻力;正弦波
0 引 言
自然界中的流体存在着各种各样的流动形态,下垫面的形状以及表面的粗糙度分别会以形状阻力(form drag)和表面摩擦阻力(skin friction)的形式对上层的流体流动造成影响,根据下垫面的形状以及粗糙度的不同,两者对流动影响的贡献也不同。而流体的流动有很大一部分是发生在下垫面不是水平光滑的情况下的,例如,丘陵地带的风场正是气体在连续的小山包上方的流动,海水对海底沙石的冲刷和搬运也是发生在高低起伏的海床上方的,更复杂的情况还有海面上的风场分布,在海气接触面上,由于风以及重力等的作用,海水无法再保持水平光滑,海面波涛起伏,海气作用相互耦合,使得海上的风场分布发生改变,从而使得按照传统规范给出的风剖面设计的海上构筑物如桥梁、海上钻井平台、海上风力发电机等面临失效的风险,甚至导致重大的财产损失和人员伤亡。因此,研究海上风场分布有着重要的现实意义,而研究海上风场分布就需要建立两项流海气相互作用模型,作为基础研究,静止的曲面渠道流中正弦波(或余弦波)形状可以近似模拟波浪的形状,对上层气体流动形成连续的阻碍,研究这种流场分布可以为更深入的研究奠定基础。
风洞实验作为研究流动的重要手段之一,一直受到广大研究者的重视。关于波浪形渠道流的研究,Hanratty和他的同事们做了大量的风洞实验,例如,Zilker,Cook &Hanratty 1977[1];Zilker& Hanratty 1979[2];Buckles,Hanratty& Adrian 1984[3],1986[4](简称 BHA);Frederick &Hanratty 1988[5];Kuzan,Hanratty&Adrian 1989[6];Hudson,Dykhno& Hanratty 1996[7],Gong et al.1996[8]。其中 BHA 实验给出了大波幅波浪渠道流平均风速和脉动风速的大量测量数据,而本文中考虑大波幅和中等波幅两种情况。
流动的理论分析(Sykes 1980[9];Hunt,Leibovich& Richards 1988[10];Belcher,Newley & Hunt 1993[11])表明,地形引起的湍流结构改变在壁面附近变异性非常大,传统对数率只在离壁面非常近的范围内成立,粘性底层的尺度要比波浪形渠道的波长小很多,通常为波长的5%,使直接捕捉这部分涡尺度变得非常困难,从而影响求解表面摩擦力的准确性,因为表面摩擦力与表面流场有着密切的联系。
近年来,随着计算机技术的发展,数值模拟的方法被广泛应用于流体计算。波浪形渠道流的 DNS (Maaß&Schumann1994[12],1996[13];De Angelis,Lombardi & Banerjee 1997[14];Cherukat et al.1998[15])成功的再现了中等雷诺数下实验室 观测到的现象,并且提供了更加详细的湍流结构数据。其中De Angelis et al.和Cherukat et al.均发现了上坡处展向速度脉动增大;De Angelis et al.采用了伪谱方法,他们在波谷的下游处(上坡处)发现了高剪应力区和条带结构的存在,同时指出准流线涡也在此处产生。大涡模拟方法也越来越多的被应用于各种复杂几何外形的流动模拟。最早利用LES技术对非水平均匀渠道流进行研究的有Krettenauer&Schumann (1992)[16],Walko,Cotton& Pielke(1992)[17],以及Dörnbrack&Schumann(1993)[18],他们对正弦波上方的湍流对流流动进行了模拟,对波浪形渠道流进行了初步的研究。Henn and Sykes(1999)[19]采用了LES研究了不同波幅的波浪形渠道流,他们也发现了上坡处展向速度脉动增大,并指出在波峰背风面存在的分离剪切层导致了波谷上方产生强湍流,他们在模拟中采用了湍动能输运方程、二阶闭合模型(Lewellen 1977[20]),并利用坐标转换将曲线坐标系,转换成直角坐标系,在此过程中,增加了数值离散的难度,加大了计算量。Calhoun and Street(2001)[21]同样采用了LES方法,不同的是他们采用的动态混合亚格子模型(dynamic mixed subgrid-scale model,Zang at al.1993[22]and Salvetti et al.1997[23])。但是以上研究都是基于顶部是无滑移条件的,而在风工程应用中,波浪上方仅仅是大气,没有顶部壁面,因此该边界条件不能适用于风工程。
本文采用大涡模拟方法,非正交网格,对散度离散进行修正,亚格子模型采用动态的Smagorinsky模型(Lilly,1992[24]),考虑到达到一定高度后,上层的流动趋于层流化,因而顶部采用自由滑移条件。
本文安排如下:首先介绍数值模型与方法,包括各个算例的网格与计算参数等;作为对数值模型的验证,接着对直渠道流进行了计算;然后详细讨论了中等波幅(2a/λ=0.1)波浪形渠道流的计算结果,包括统计后的平均流场和瞬态流场;最后给出了大波幅(2a/λ= 0.2)波浪形渠道流的部分计算结果,并作了对比。
1 数值模型与方法
1.1 LES数值模型
采用直角坐标系,x、y、z分别为流向、竖向和展向,如图1所示。底面的高程可以表示成x、y的函数(实际只是x的函数),即h(x,y)=a cos(2πx/λ),其中a为波幅,λ为波长。过滤后的速度矢量为u=(u,v,w),直角坐标为x=(x,y,z)。过滤后的Navier-Stokes方程可以表示为:

图1 波浪形渠道流示意图Fig.1 Sketch of channel with a periodic wavy wall

连续性方程为:

其中,动量方程(1)中的6项分别为瞬态项、对流项、压力源项、耗散项、亚格子应力项和驱动力项,P= (Px,0,0),Px是x 方向的驱 动力,计算过程中根 据平均速度Ub来调整Px,以保证Ub=1为定值。采用Boussinesq涡粘假设 (Boussinesq eddy viscosity assumption),令

因此,在程序中定义
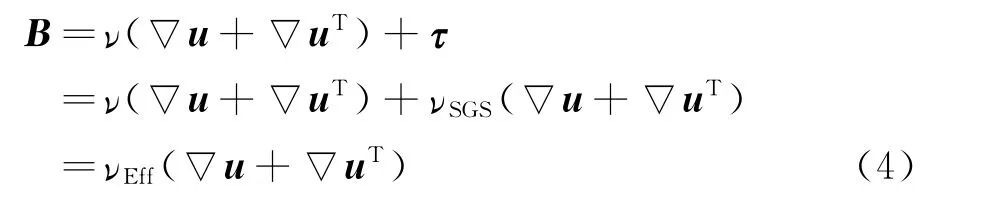
方程 (1)可以写成

其中νEff称为有效粘性系数,νSGS为亚格 子湍动粘 度,本文选用动态的Smagorinsky亚格子模型。模型采用有限体积法,对流项和扩散项采用二阶中心差分,对梯度项进行网格非正交修正,时间导数项采用二阶向后差分,网格采用结构化网格,压力速度耦合采用PISO算法。
1.2 网格与计算参数
本文首先计算了两个直渠道流的算例,分别为FC1和FC2(FC=Flat Channel),渠道尺寸均为(L,W,H)=(4π,2π,2),见图1,对直渠道流,波长λ=∞,基于平均流速和半槽宽的雷诺数Reb=0.5HUb/ν= 3250,其中,平均流速

u是流向速度。FC1流向、竖向和展向网格数均为64,流向和展向网格均匀分布,竖向网格按余弦函数分布,即

FC2流向、竖向和展向网格数均为96,流向和展向网格均匀分布,竖向网格按双曲正切函数分布。直渠道流的边界条件设置为:下底面和上顶面均为无滑移条件,四个侧面均为周期条件。亚格子模型采用动态的Smagorinsky模型,空间平均采用沿流向和展向平均,时间平均取200L/Ub。
波浪形渠道流两个算例分别为WC1、WC2(WC =Wavy Channel),WC1的计算域尺寸为(L,W,H)=(4,2,1),如图1所示,H=1为平均槽宽,波高a= 0.05,波长λ=1,波陡为ka=2πa/λ≈0.314,与 Maaß &Schumann(1996)DNS相同,竖向最小、最大无量纲网格高度分别为0.001和0.05,无量纲化采用如下公式

其中,h为底面高程,h(x,y)=a cos(2πx/λ),竖向网格的伸展率约为1.05。基于平均流速和平均槽宽的雷诺数Reb=HUb/ν=6760。WC2的计算域尺寸为(L,W,H′)=(4.286,1.072,1.072),如图1,平均槽宽H= H′-a=1.072-0.01072=0.9648,H′为最大槽宽,波高a=0.1072,波长λ=1.072,波陡为ka=2πa/λ≈0.628,与Henn and Sykes(1999)LES的BHA1L算例及实验BHA相同,竖向最小、最大无量纲网格高度分别为0.001和0.05,Reb=H′Ub/ν=6760。两个算例的网格数均为(Nx,Ny,Nz)=(192,96,96),网格示意图如图2所示。图2中,由于网格太密,网格线采用每四根网格线一显示。两个算例底面均为四个波长的余弦波,如图1所示,流向长度为L,展向长度和波长分别为W 和λ。四个侧面均采用周期条件,底面采用无滑移条件,而为了风工程研究的需要,顶面应该是与大气接触的,不存在固定壁面,所以应采用自由滑移条件,这是与以往文献中的边界条件均不同的(Nakayama 2002除外),顶面边界条件的不同使得平均风剖面的结果在0.5H 以上的部分与以往的数值模拟和风洞模拟有所不同。
计算结果的平均先对时间进行,平均采用的时间长度为100H/Ub,此处的平均流速定义为这里均控制Ub=1,再对所有展向取平均,最后对四个周期相同相位的数值取平均。


图2 波浪形渠道流网格示意图Fig.2 Grids of the wavy channel(Every four grid lines shown)
2 结果分析
2.1 直流渠道
直渠道流的研究比较广泛,结果也比较成熟,有大量的DNS数据和实验数据可供参照对比,是检验数值算法的很好算例。为了验证数值方法的可靠性,本文首先采用相同的LES模型(包括离散方法,湍流模型)对直渠道流进行了模拟。无量纲的流向平均速度剖面如图3(a)所示,与KMM (Kim,Moin and Moser 1987[25])DNS对比,显示了很好的符合性,在粘性地层y+<10的范围内,LES结果与 DNS结果差别很小,基本满足u+=y+的壁面率;在y+>20,LES的速度略大于KMM,与Eckelmann(1974)风洞实验数据吻合得很好,FC2在对数层的速度值略低于FC1,差别不大,说明了网格的精度足够,数值计算结果是收敛的。其中,y+=yuτ/ν,u+=u/uτ。
图3(b、c)显示了速度脉动沿槽道高度方向的分布,速度脉动均采用壁面剪切速度uτ无量纲化,与KMM 相比,剖面的整体形状符合的比较好,两个算例的最大流向速度脉动均出现在y+=12处,与产生最大湍动能的位置相符。三个方向脉动速度的峰值位置均与KMM 相同,在壁面的地方吻合较好,但是在y+≈5以外 LES算得的流向速度脉动值要略大于KMM的DNS值,FC2与Eckelmann实验值较吻合,而展向和竖向速度脉动则要略小于DNS值,在壁面附近数值模拟的值都要明显小于实验值,实验测得的竖向、展向脉动在壁面附近增长得更快,展向脉动速度的峰值更加明显。图4雷诺应力也显示了很好的吻合性。其中,

图3 近壁速度分布Fig.3 Velocity distribution near the wall

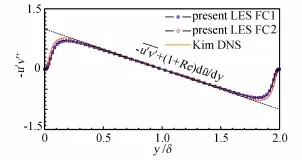
图4 雷诺应力Fig.4 Reynolds stress
2.2 中等波幅波浪形渠道流
2.2.1 平均流场
由于波浪形下表面沿展向是均匀不变的,沿流向的四个波长的对应位置又呈现出周期性变化的特点,所以统计特性在展向和同相位处是统计均匀的,故所有的统计量取均值的方法都是首先对时间平均,再沿展向平均,最后对同相位平均。所有的图形都是统计后的量在竖直平面内绘出的。
根据计算结果,波浪形下表面对上层流体流动平均特性的影响在0.3倍渠道高度以下(称为内区,inner region)影响明显,此高度往上(称为外区,outer region),流体受到的影响明显减弱,平均速度剖面趋于一致,如图6、图7 所示(y/H=0.3对应y+≈200),故云图只绘出了内区,即0.3H 以下部分。流向平均速度云图如图5所示,从图中可以看出,分离点(separation point)在x/λ=0.14,再附点(reattachment point)位于x/λ=0.65,在分离点与再附点之间存在着一个回流区,形状呈扁长的卵状,回流区中心位于比波谷略靠上游的位置,相应的无量纲坐标为(0.48,-0.037),对应的平均速度最小值约为-0.08。整个回流区的长度约为0.5λ,回流区覆盖波谷上游(波峰的背风面,或称下坡面)0.36λ,覆盖波谷下游(上坡面)0.15λ,最大高度约为0.04H。回流区的形状由平均流线图6也可以清楚地看出。波谷上方速度的竖向梯度较小,变化较缓慢,而在波峰处以及邻近的两侧等值线密集,速度的竖向梯度很大,尤其是0~0.1λ和0.7λ~1.0λ范围内,0.1H 往上部分,速度变化匀缓。将0.7λ~1.1λ区间贴近壁面的部分称为边界层区(boundary layer region),边界层区的显著特点是速度的展向变化大、展向脉动大,这在后面的瞬态速度向量图和展向脉动图中可以看出。

图5 平均流向速度云图Fig.5 Mean streamwise velocity contour

图6 平均流线图Fig.6 Mean streamlines
流向平均速度剖面如图7所示,图中蓝色带星号的是当前的LES结果,黑色带圆圈的是Maaß等人的DNS 结果,粉色实线是 Nakayama[26]的 LES 结果,由图可见速度剖面在0.5倍高度以下吻合得很好,由于 Maaß顶部采用的是无滑移条件,顶部速度等于0,而本文为模拟大气边界层,顶部采用的是自由滑移条件,顶部速度最大,约为1.19,Maaß 的DNS中,由于上下部都受到壁面摩擦阻力作用,剖面在渠道中部更趋于外凸。图中每隔约0.1λ绘制一个剖面,为避免相邻的剖面交错在一起,图中速度的值缩小了12倍,可以看出剖面的变化趋势与云图的结论一致,波峰处的剖面形状更接近于直渠道流,而在波峰背风面的分离点之后,由于负压力梯度的影响,速度剖面开始出现反弯,在接近壁面处的速度为负值,一直到再附点,壁面附近的负速度消失,即回流区部分。同样,剖面形状也显示出波峰处由于迎风截面受到压缩,速度加速,底部速度梯度很大。波谷处的速度剖面变化则相对平缓。

图7 平均流向速度剖面Fig.7 Mean streamwise velocity over the first wavelength
无量纲化以后的流向速度剖面如图8所示,每隔0.1λ绘制一个剖面,为便于对比,相隔0.5λ的剖面绘在一起,图中带圆圈的是前半个波长上的剖面,带三角的是后半个波长上的剖面,蓝色实线是平均剖面,无量纲化时采用沿下表面平均后的uτ。Maaß的DNS只绘出了0.5H 以下的部分,可以看出渠道中部,其速度要比本文偏大,这与上边界条件设置是一致的。相隔半个波长的两个剖面显示出很强的规律性,即他们基本关于平均速度剖面对称,分布在其上下两侧。在x=0.1、0.7、0.8、0.9、1.0处的5个剖面落在回流区之外,速度均不出现负值;而其余5个剖面均落在回流区,近壁速度先负后正。外区(y>0.3,y+>200)部分,速度剖面基本重合,受下表面的影响可以忽略。由外区的直线关系可以看出,外区的速度剖面还是满足对数率的,只是此时由于采用的不是当地摩擦速度,而是沿整个下表面平均后的摩擦速度,对数率的系数发生了变化。
平均竖向速度云图如图9所示,可以分为三个区域,正速度区被负速度区分隔成了两块,第一块位于负速度区底部的回流区内,区间范围为0.14λ~0.5λ,起点与分离点重合,终点位于波谷;第二块位于边界层区内,范围为0.65λ~1.0λ,起点与再附点重合,由于受到上坡的挤压,平均竖向 速度变正,竖向速度迅速的从0增加到峰值0.108,位置位于波峰迎风侧,无量纲位置坐标为(0.86,0.05),高度与波峰齐平,之后又向波峰处迅速减小,在峰顶附近减为0;然后竖向速度沿下坡缓慢的变为向下的速度,速度绝对值逐渐增大,在波谷上方的下游出现最值-0.042,无量纲坐标为(0.53,0.05),高度与波峰高程齐平,之后又逐渐由负变正,负值区的范围为0~0.65λ,负速度区的覆盖范围要大于正速度区,正负最值的比约为2.5。

图8 无量纲平均流向速度剖面Fig.8 Normalized mean streamwise velocity profiles
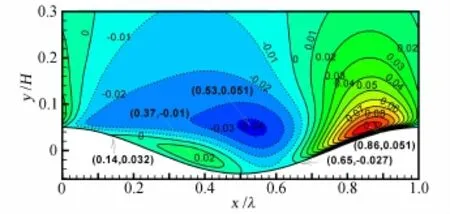
图9 平均竖向速度云图Fig.9 Mean vertical velocity contour
从平均竖向速度剖面图10中,也可以看出速度的3个区域,在回流区底部竖向速度有正值,回流区上方速度变为负值。竖向速度在冲击带达到最大值,冲击带的概念见下文展向速度脉动部分。

图10 平均竖向速度剖面图Fig.10 Mean vertical velocity profiles
相比平均流向速度和竖向速度,平均展向速度尽管在波谷上方以及边界层区也会出现峰值,平均速度剖面的波动性很大,其他规律不是那么明显。
展向速度沿展向的变化较大,呈现正负交替的现象,故沿展向作平均后的结果会使得一些信息丧失,从而研究展向速度的平均值意义不大,本文将在下文的瞬态速度场中研究展向速度的分布规律。
与平均风速一样,平均后的脉动特性也显示了很强的规律性。图11(a)为平均流向脉动速度平方的云图,流向脉动速度平方在波谷上方出现一个最大值区域,起始点位置基本与分离点相同,无量纲坐标为(0.145,0.068),终点为(0.82,0.039),峰值为0.0545,峰值点位于波谷上方,约0.8倍波幅高度处,坐标为(0.48,0.041)。脉动值在壁面附近迅速减小,尤其是边界层区0.65λ~1.1λ范围内,脉动速度梯度很大,回流区梯度相对较小,壁面处减为0。从剖面角度看,流向各个位置处,出现峰值的高度大约都在0.1H 以下,边界层区的峰值位置高度非常接近壁面,小于0.01H,波峰处的峰值高度约为0.01H,波谷处约为0.04H。

图11 平均脉动速度平方云图Fig.11 Mean velocity fluctuation
与流向、竖向脉动不同,平均展向速度脉动的最大值出现在上坡处,如图11(c)所示,最大值为0.0272,是流向最大值的0.5倍,是竖向最大值的1.8倍。最大 值 出现 的位 置坐 标为 (0.73,0.013),离壁面非常近。可以形象地将再附点到波峰之前的这段上坡区域叫做冲击带 (impact zone),当波幅增大,2a/λ=0.2时,展向脉动甚至超过了流向脉动,这在Henn and Skyes,De Angelis,Cherukat等人的研究中均有体现。这意味着在冲击带存在着与波陡有关的局部能量产生机理。
平均展向涡量ωz云图如图12所示,在0.8H 以下涡量明显,壁面附近涡量出现正负峰值,0.8H 以上,涡量接近于0。壁面附近,涡量以回流区为界,分成正负涡量区,回流区以内,涡量为正值,即涡逆时针旋转,无滑移的壁面壁面对流体施加的剪力作用沿壁面切线方向向左,最大值约为21,位于波谷处。涡量负值区则分布在回流区两侧,并且在分离点处向上抬升,拖出一条很宽的尾巴,一直蔓延到波谷上方,最小值则以0.9λ为中心,相应的最小值约为-88,此处位于冲击带,负涡量的绝对值约为正涡量的4倍。

图12 平均展向涡量ωz云图Fig.12 Mean spanwise vortictyωz
统计量在竖直面内的分布与下表面的几何形状(波长/波幅)有着密切的联系,几何形状在很大程度上决定了回流区的形状与位置,下表面相对波幅减小甚至会导致回流区消失,极限情况就是直渠道流(2a/λ=0),Henn and Skyes的研究中,2a/λ=0.031时就未出现回流区。
从脉动速度的云图可以看出,流向速度脉动是占主导地位的,所以湍动能的分布更接近于流向速度脉动,如图13所示,峰值出现在波谷上方,高度比波峰高度略高,最大值为0.029。
表面的摩阻力以及表面压力也是重要的空气动力学特性指标之一,许多领域都很关心与流体接触面的受力,海洋学中研究风浪相互作用时海面的拖拽系数,再如风工程领域关心的大气边界层粗糙度类别,实际就是表面摩阻力的工程化算法。故本文对波浪形下表面的表面摩阻力τw和表面压力pw作了研究,根据牛顿液体的应力应变关系τ0=μδ¯u/δy,其中δ¯u/δy是第一层网格处的平均速度剪切率,这里采用τw=τ0/(0.5ρU2b)进 行 无量 纲 化,Ub=1为 平 均 来 流速度。τw沿流向的分布如图14(a)所示,在x/λ≈0.14~0.66之间,τw为负值,此区间与回流区区间简本重合,再次说明了回流区流体是沿顺时针方向运动的,流体対壁面的作用力是向左的,从分离点开始,负的摩阻力逐渐增大,在0.2λ~0.35λ之间增长缓慢,几乎不变,负的最大摩阻力出现在波谷x/λ=0.5处,值为-0.0047,之后一直减小,大约在再附点处减到0。进入冲击带之后,摩阻力变正,由于此处速度梯度大,摩阻力也大,且增长迅速,最大值0.0223出现在x/λ=0.917处,之后一直减小到分离点的0值。
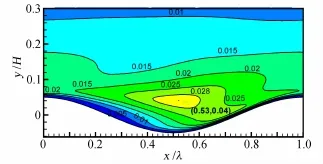
图13 平均湍动能k云图Fig.13 Mean kinetic energy k

图14 壁面平均压力平均摩阻力τw与pw沿流向的分布Fig.14 Mean surface drag and pressure distribution along x-direction
壁面平均压力pw的展向分布如图14(b)所示,这里pw=(p-pref)/0.5ρU2b,正值 区 间 为 0.419λ~0.872λ,其余为负值区间,最大正压 0.154,位于0.71λ处,最大负压-0.14,位于波峰处。在靠近分离点处,pw曲线的斜率明显降低。
pw与形状阻力对应,τw与表面摩擦阻力对应,由图可见,形状阻力要比表面摩擦阻力大一个数量级。2.2.2 瞬态流场
这里采用λ2识别法来识别涡,其识别标准是S2+Ω2的特征值有两个为负值。图15是采用λ2识别法来识别近壁涡结构的可视化图形,图中显示了λ2=-20的等值面。由图可知,流向涡占主导地位,是主要的涡结构形式,这些流向涡或多或少与x轴存在一定的交角,故可称之为准流向涡,他们绝大多数起始于上坡面(冲击带),跨过波峰向下游的波谷延伸。图中也可见到展向涡,展向涡的尺度相对较小。有些地方甚至可以见到发卡涡,这种拟序结构(coherent structure)在直渠道流中很常见。

图15 λ2等值面图Fig.15 Iso-surface ofλ2=-20
图16为瞬态速度场垂直于流向的切片,切片位于x/λ=1.75,在冲击带上方,图中显示的高度为0.3H 以下。图中展向的运动速度明显,流场中出现一系列类似涡形态的展向运动结构,贴近壁面处的展向“类涡”运动最为明显。这种流动可以形象地称作次生流动,主要出现在冲击带上方。由于壁面的阻挡和反射作用,使得近壁面处的竖向脉动衰减,而展向没有壁面阻挡,这部分湍动能会注入到展向脉动中,即展向脉动会相应的增加,这也可能是壁面附近展向速度|w′|要比竖向速度|v′|大的原因。

图16 瞬态速度场x/λ=1.75,z=0.5λ~1.5λFig.16 Slice of instantaneous velocity vectors at x/λ=1.75
2.3 大波幅波浪形渠道流
当波幅增大后,流场的流动形态会发生变化,为了对比,以下给出了 WC2(2a/λ=0.2)的部分流场情况。
由图17(a)和图17(b)可以看出,由于波幅的增大,回流区更加饱满,覆盖了两个波峰之间的绝大部分,分离点由0.14前移到0.079,再附点从0.65延后到0.766;波幅增大后,正负峰值速度的绝对值均显著增大,最大负速度由-0.08变为-0.218,顶部最大速度也由1.19增大到1.41;流线图中,旋涡更加丰满,涡顶部几乎保持水平,且位置与波峰齐平。

图17 大波幅平均统计结果Fig.17 Averaged results of the large amplitude wavy channel
平均竖向速度依然分为三个区域,如图17(c)所示,最大正负值速度分别由-0.042和0.108变为-0.09和0.16,底部的正速度区面积增大,从变长的卵形变为近似的直角三角形,相应的负值区域有所减小;正峰值位置变化不大,负峰值后移,且更贴近壁面。图17(d)平均展向脉动的峰值仍然位于冲击带上方,位置略微后移,峰值由0.0272变为0.072,且超过了流向脉动的峰值0.065和竖向脉动峰值0.028,为三个方向脉动最大的方向,壁面对三个方向脉动能量分配的影响更显著。
3 结论与展望
本文采用LES方法对带有余弦波形状底面、自由滑移顶面的渠道流进行了模拟,得到的结论总结如下:
(1)统计结果表明波浪形下表面通过其波幅和波长影响着流场在空间上的分布形态,根据受壁面形状影响的大小,在竖向可将流场分成内区和外区,他们以y/H=0.3(y+≈200)为界,内区受壁面形状影响很大;外区基本不受壁面形状的影响,外区在流向不同位置的平均速度剖面趋于一致。
(2)分离点位于x/λ=0.14,再附点位于x/λ= 0.65,分离点与再附点之间为回流区,长度约为半个波长,位置偏上游;流向平均速度剖面在回流区会有反弯,回流区的平均竖向速度基本为正,回流区上方的平均竖向速度为负。
(3)再附点之后的上坡面到波峰偏下游为冲击带,此处存在着一些特殊的物理现象:流向速度在壁面处的梯度很大,过流面积的压缩使流体加速;冲击带上方存在一个正的竖向速度区,且在(0.86,0.05)达到峰值;更显著的特征是展向脉动速度在冲击带上方达到峰值,且超过竖向脉动,约为流向脉动的一半;负值涡量(涡沿顺时针旋转)在冲击带上方有最值,并且是最大正值涡量(波谷处)的4倍。
(4)在内区,相隔半个波长的无量纲化平均速度剖面基本关于对整个场平均的平均速度剖面对称,且不再符合传统的x+=y+;在外区(y+>200),平均速度剖面依然符合对数率;内区的速度在波峰后减速、变负,然后再加速变正。(5)波谷上方是平均流向脉动竖向脉动以及湍动能k 的最值区(最大值)。
(6)表面摩阻力τw沿流向的分布规律也比较显著,负摩阻力区间基本与回流区一致,最大正摩阻力位于冲击带,最大负摩阻力位于波谷处,且正负最值比约为5;表面压力pw比表面摩阻力τw大一个数量级,对阻力的贡献占主导地位。
(7)瞬态流场中,壁面附近是涡的主要存在区域,从λ2等值面图中可以看到准流向的拟序结构;冲击带上方存在着类似涡形态的次生展向流动,近壁展向速度在展向层正负交替分布,特征长度约为1/3λ。
(8)波幅增大后,流动分离更加明显,回流区面积增大,形状更加饱满,正负峰值速度的绝对值均显著增大;展向脉动显著增加,并超过了流向脉动,壁面对三个方向脉动能量分配的影响更加显著。
本文是为研究风浪耦合作用下的海上风剖面而做的基础研究,进一步深入的研究包括:
(1)移动下边界波浪形渠道流的研究,考虑下表面作强制平移运动或者波动对上层风场的影响(后者为相位传播,质点不“随波逐流”,更接近真实海浪的运动),可以研究波龄对拖拽力的影响,然而强迫运动也是一种理想化的模型,不能考虑风浪的耦合作用,即风-浪之间动量的互相传递,也不能考虑波浪的复杂形态,仅仅把浪当作单一的简谐波考虑。
(2)建立气液两相流模型,考虑风浪的相互耦合,甚至考虑波浪的复杂形态,甚至考虑在强风作用下波浪的破碎对拖拽力的影响。
[1] ZILKER D P,COOK G W,HANRATTY T J.Influence of the amplitude of a solid wavy wall on a turbulent flow.Part 1.Nonseparated flows[J].J.Fluid Mech.,1977,82:29-51.
[2] ZILKER D P,HANRATTY T J.Influence of the amplitude of a solid wavy wall on a turbulent flow.Part 2.Separated flows [J].J.Fluid Mech.,1979,90:257-271.
[3] BUCKLES J,HANRATTY T J,ADRIAN R J.Turbulent flow over large-amplitude wavy surfaces[J].J.Fluid Mech.,1984,140:27-44.
[4] BUCKLES J,HANRATTY T J,ADRIAN R J.Separated turbulent flow over a small amplitude wave.Laser Anemometry in Fluid Mechanics[M]{II(ed.R.J.Adrian,D.F.G.Durao,F.Durst,H.Mishina &J.H.Whitelaw),1986:347-357.Ladoan,Lisbon.
[5] FREDERICK K A,HANRATTY T J.Velocity measurements for a turbulent nonseparated flow over solid waves[J].Exps. Fluids,1988,6:477-486.
[6] KUZAN J D,HANRATTY T J,ADRIAN R J.Turbulent flows with incipient separation over solid waves[J].Exps.Fluids,1989,7:88-98.
[7] HUDSON J D,DYKHNO L,HANRATTY T J.Turbulence production in flow over a wavy wall[J].Exps.Fluids,1996,20:257-265.
[8] GONG W,TAYLOR P A,DÖRNBRACK A.Turbulent boundarylayer flow over fixed aerodynamically rough two-dimensional sinusoidal waves[J].J.Fluid Mech.,1996,312:1-37.
[9] SYKES R I.An asymptotic theory of incompressible turbulent boundary-layer flow over a small hump[J].J.Fluid Mech.,1980,101:647-670.
[10]HUNT J C R,LEIBOVICH S,RICHARDS K J.Turbulent shear flow over low hills[J].Q.J.R.Met.Soc.,1988,114:1435-1470.
[11]BELCHER S E,NEWLEY T M J,HUNT J C R.The drag on an undulating surface induced by the flow of a turbulent boundary layer[J].J.Fluid Mech.,1993,249:557-596.
[12]MAAßC,SCHUMANN U.Numerical simulation of turbulent flow over a wavy boundary.Direct and Large Eddy Simulation-I[M].(ed.P.R.Voke,L.Kleiser&J.P.Chollet).Kluwer,1994.
[13]MAAßC,SCHUMANN U.Direct numerical simulation of separated turbulent flow over a wavy boundary.Flow Simulation with Higher Performance Computers-II(ed.E.H.Hirschel)[M].1996,227-241.
[14]DE ANGELIS V,LOMBARDI P,BANERJEE S.Direct numerical simulation of turbulent flow over a wavy wall[J].Phys.Fluids,1997,9:2429-2442.
[15]CHERUKAT P,NA Y,HANRATTY T J,et al.Direct numerical simulation of a fully developed turbulent flow over a wavy wall[J].Theoret.Comput.Fluid Dyn.,1998,11:109-134.
[16]KRETTENAUER K,SCHUMANN U.Numerical solution of turbulent convection over wavy terrain[J].J.Fluid Mech.,1992,237:261-300.
[17]WALKO R L,COTTON W R,PIELKE R A.Large-eddy simulations of the effects of hilly terrain on the convective boundary layer[J].Boundary-Layer Met.,1992,58:133-150.
[18]DÖRNBRACK A,SCHUMANN U.Numerical simulation of turbulent convective flow over wavy terrain[J].Boundary-Layer Met.,1993,65:323-355.
[19]DOUGLAS S.HENN and R.IAN SKYES.Large-eddy simulation of flow over wavy surfaces[J].J.Fluid Mech,1999,383:75-112.
[20]LEWELLEN W.Use of invariant modeling:Handbook of Turbulence,Plenum[M].New York,1977.
[21]RONALD JCalhoun,ROBERT L Street.Turbulent flow over a wavy surface:Neutral case[J].Journal of Geophysical Research,2001,106(C5):9277-9293.
[22]ZANG Y,STREET R,KOSEFF J.A dynamic mixed subgridscale model and its application to turbulent recirculating flow [J].Phys.Fluids,1993,5:3186-3196.
[23]SALVETTI M,ZANG Y,STREET R,et al.Large eddy simulation of free-surface decaying turbulence with dynamic subgridscale models[J].Phys.Fluids,1997,9:2405-2419.
[24]LILLY D K.A proposed modification of the Germano subgridscale closure method[J].Phys.Fluids A,1992,4:633-635.
[25]JOHN KIM,PARVIZ MOIN,ROBERT MOSER.Turbulent statistics in fully developed channel flow at low Reynolds number[J].J.Fluid Mech.,1987,177:133-166.
[26]NAKAYAMA A,SAKIO K.Simulation of flows over wavy rough boundaries[R].Center for Turbulence Research Annual Research Briefs,2002.
Large-eddy simulation of fully developed turbulent flow over a wavy surface
SUN Liming,CAO Shuyang,LI Ming,YANG Qing,ZHANG Enzhen
(State Key Laboratory of Disaster Reduction in Civil Engineering,Tongji University,Shanghai 200092,China)
Large eddy simulation(LES)is used to study flow over a sinusoidal bottom wall,with amplitude-wavelength ratio 2a/λ=0.1 and bulk velocity based Reynolds number Reb=6760.Different from a conventional flat channel,flow over a wavy lower surface is affected by the bottom wall in terms of form drag,leading to the change of both mean and instantaneous fields.Wall bounded flow turns into a separation flow with the increasing of Reynolds number,changing the way in which momentum flux transports and mixes.Statistical properties,transient flow fields as well as surface drag are studied.Averaged fields and turbulent structures are different from those of a flat channel.Distribution and shape of streamwise vortex are closely related to the configuration of the lower surface.Comparison of averaged fields with 2a/λ=0.2 shows the dependence of flow characteristics on the wave steepness.
LES;wavy channel;mean wind profile;channel flow;drag force;sinusoidal wave
O357.5
Adoi:10.7638/kqdlxxb-2012.0172
0258-1825(2014)04-0534-10
2012-10-24;
2012-12-27
国家自然科学基金 (50978202);国家自然科学基金中日科研国际合作项目 (51021140005)
孙丽明(1986),男,江苏泰州人,硕士,研究方向:桥梁结构抗风,强风作用下海上风剖面数值模拟.E-mail:sunliming59045@126.com
曹曙阳(1966),男,江苏姜堰人,博士、同济大学特聘教授,国际风工程协会秘书长.E-mail:shuyang@tongji.edu.cn
孙丽明,曹曙阳,李明,等.考虑波浪形底面影响的边界层风场大涡模拟[J].空气动力学学报,2014,32(4):534-543.
10.7638/kqdlxxb-2012.0172. SUN L M,CAO S Y,LI M,et al.Large-eddy simulation of fully developed turbulent flow over a wavy surface[J].ACTA Aerodynamica Sinica,2014,32(4):534-543.
