晶圆清洗机无刷电机齿槽转矩的仿真分析

李新华，杜成飞，黄贤蕾，杨垂恭

（1湖北工业大学电气与电子工程学院，湖北武汉 430068；2台湾阪神电机有限公司，台湾）

晶圆清洗机无刷电机齿槽转矩的仿真分析

李新华1，杜成飞1，黄贤蕾1，杨垂恭2

（1湖北工业大学电气与电子工程学院，湖北武汉 430068；2台湾阪神电机有限公司，台湾）

齿槽转矩对无刷电机低速性能产生重要影响.采用计算机仿真方法研究晶圆清洗机无刷电机的齿槽转矩问题，包括极槽配合、磁极以及定子斜槽／转子斜极对无刷电机齿槽转矩的影响，在此基础上提出晶圆清洗机无刷电机的优化设计方案.

晶圆清洗机；无刷电机；齿槽转矩；脉动转矩；计算机仿真

随着永磁无刷直流电动机（以下简称无刷电机）应用场合的不断拓宽，对其性能要求也越来越高.如晶圆清洗机驱动用无刷电机最高转速3 000r／min，低速启动要平顺，并能在25r／min持续运转.因此，晶圆清洗机无刷电机要兼顾高、低速时的性能要求，特别是低速时转矩要平稳，尽可能地降低脉动转矩.无刷电机脉动转矩包含齿槽转矩和纹波转矩［1］.齿槽转矩是由转子磁极与定子齿槽之间磁阻的变化引起，即使定子绕组没有通电也会产生齿槽转矩；纹波转矩则是由定子电流与转子磁极之间的相互作用而产生［2］.前者取决于电机结构，后者与电机控制有关.无刷电机的低速度性能不好，主要是齿槽转矩比较大，影响电机运行的平稳性，严重时导致无刷电机无法正常运转.

本文以晶圆清洗机750W无刷电机为例，采用计算机仿真方法研究极槽配合、磁极以及定子斜槽／转子斜极对无刷电机脉动转矩，特别是齿槽转矩的影响.分别采用场－路联合（以下简称为FCU）仿真和Maxwell 2－D有限元（以下简称为2－D）仿真方法.所谓FCU仿真方法，即通过ANSYS Simplorer的有限元链接功能，将ANSYS Maxwell 2－D模块和ANSYS Simplorer模块连接起来进行实时数据交换与计算［3］，显然，FCU仿真结果中包含有纹波分量.定子斜槽，或转子斜极则采用分段模型的2－D近似仿真方法，也就是把电机沿着轴向均分为若干段，每段近似为一直槽／直极电机，再使用2－D来进行仿真分析［4］.

1 极槽配合

现在无刷电机比较多地采用分数槽绕组组合定子铁心结构，整数槽绕组应用越来越少.分数槽绕组简化电机结构和制造工艺，而整数槽在改善无刷电机低速性能方面有一定优势.图1是极槽配合分别为8极12槽（每极每相槽数q＝0.5）、6极18槽（q＝1）和4极24槽（q＝2）无刷电机的仿真模型（假定模型中转子磁极为等厚、平行充磁且相互之间无间隙）.图2、3是三种极槽配合无刷电机电磁转矩FCU仿真波形（25r／min）和2－D FEM有限元齿槽转矩仿真波形，表1为FCU仿真和2－D仿真计算出的转矩结果.

图1 三种极槽配合无刷电机的仿真模型

图2 不同极槽配合的FCU仿真波形

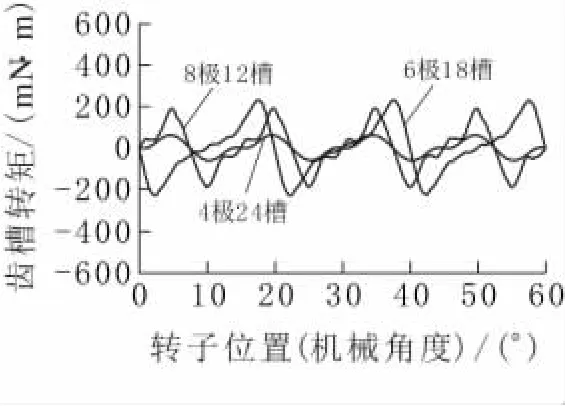
图3 不同极槽配合的2－D仿真波形

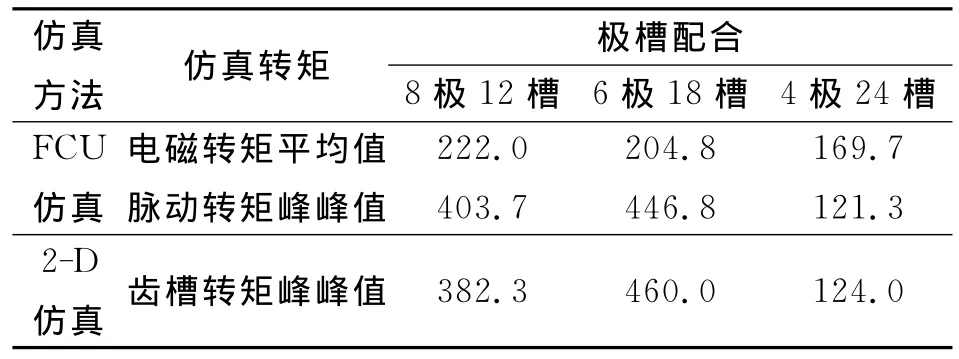
表1 三种极槽配合无刷电机的转矩仿真结果mN·m

表中的脉动／齿槽转矩峰峰值 ＝ 转矩最大值－转矩最小值，下同

从表1可知，FCU仿真计算出的脉动转矩峰峰值与2－D仿真计算出的齿槽转矩峰峰值相差不大，波形也比较接近.由于FCU仿真在逆变桥外加电压，因此转矩波形中存在平均电磁转矩分量，8极12槽无刷电机的平均电磁转矩最大，6极18槽次之，4极24槽最小；另一方面，6极18槽无刷电机齿槽转矩峰峰值最大，8极12槽次之，4极24槽最小，而且最大和最小相差3.71倍.可见，极槽配合对无刷电机齿槽转矩影响非常大，如果要求无刷电机有良好的低速性能，应选择少极多槽配合的整数槽绕组，如4极24槽配合方案（下面分析均采用此极槽配合）.

值得注意的是表中脉动转矩峰峰值小于齿槽转矩峰峰值.产生这一现象的原因在于无刷电机低速时换相时刻的尖峰转矩与齿槽转矩反相位，使得合成脉动转矩峰值减小，见图4.图中电磁转矩是去掉平均转矩后的波形，主要成分为齿槽转矩.高速时由于电感作用，换相时刻的尖峰转矩与齿槽转矩同相位，使得合成脉动转矩峰值增加.

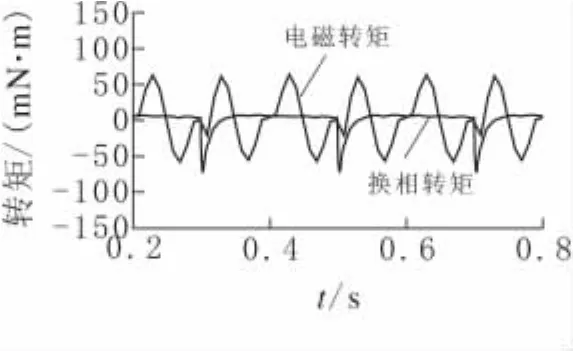
图4 低速时的换相转矩与齿槽转矩

2 磁极

无刷电机的磁极形状、极弧系数以及充磁方向与气隙磁密波形有着密切关系，同时对转矩脉动也会产生重要影响［5］，下面分别加以讨论.

2.1 等厚、等径磁极

对等厚和等径磁极（假定平行充磁且相互之间无间隙）无刷电机进行空载转矩仿真分析，仿真模型如图5所示.图6、7分别是等厚、等径磁极无刷电机电磁转矩的FCU仿真波形（25r／min）和齿槽转矩的2－D仿真波形，表2分别为FCU仿真和2－D仿真计算出的转矩结果.

图5 等径等厚磁极无刷电机的1／4仿真模型

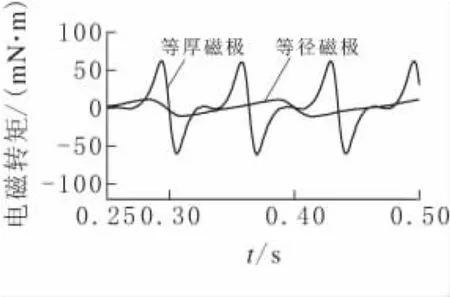
图6 等厚等径磁极的FCU仿真波形

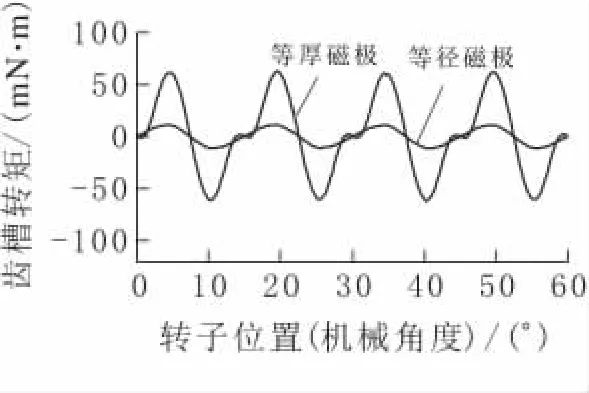
图7 等厚等径磁极的2－D仿真波形

表2 等厚、等径磁极无刷电机的转矩仿真结果mN·m

从表2可知，等径磁极无刷电机齿槽转矩峰峰值比等厚磁极的小，两者相差5.5倍，因此，对于低速平稳性能要求高的无刷电机应选择等径磁极；另一方面，FCU仿真和2－D仿真计算出的脉动转矩峰峰值和齿槽转矩峰峰值基本相等，原因在于此时电机空载，换相脉动转矩很小，FCU仿真的脉动转矩基本为齿槽转矩所致.

2.2 极弧系数

对不同极弧系数（假定等径磁极、径向充磁）无刷电机进行转矩仿真分析，图8给出了不同极弧系数与转矩峰峰值之间的关系曲线.可见，如果磁极采用径向充磁，当极弧系数为0.875时无刷电机的齿槽转矩峰峰值最小.从降低无刷电机齿槽转矩方面考虑，应选择0.875的极弧系数比较合理.

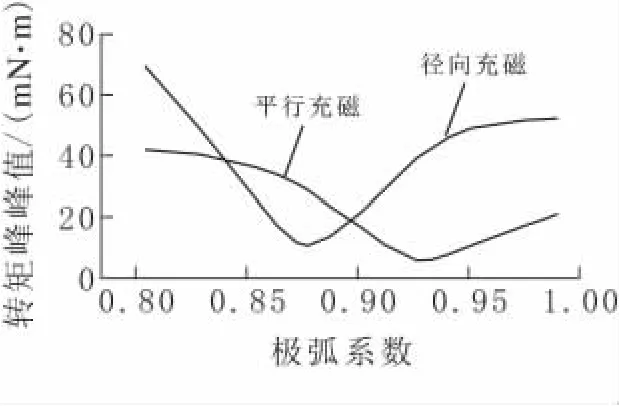
图8 极弧系数与转矩峰峰值之间的关系曲线

2.3 充磁方向

磁极常用的充磁方向有平行和径向充磁两种.类似方法分析平行充磁时无刷电机不同极弧系数与转矩峰峰值之间的关系，当极弧系数等于0.925时无刷电机齿槽转矩的峰峰值最小（见图8）.可见，无刷电机齿槽转矩峰峰值不仅与极弧系数有关，还与充磁方向有关.

对平行和径向充磁磁极（假定等径磁极、极弧系数分别为0.875和0.925）无刷电机进行转矩仿真分析，图9、10分别是平行和径向充磁磁极无刷电机齿槽转矩仿真波形，表3为不同充磁方向齿槽转矩的峰峰值.

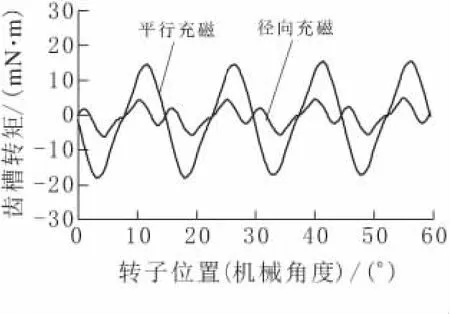
图9 极弧系数0.875时齿槽转矩仿真波形

图10 极弧系数0.925时齿槽转矩仿真波形

如果磁极采用平行充磁，极弧系数为0.925时无刷电机的齿槽转矩峰峰值只有6.8mN·m，比径向充磁，极弧系数为0.875时齿槽转矩峰峰值下降60%，但如果磁极用径向充磁，齿槽转矩峰峰值却是最大的.

磁极优化前，4极24槽无刷电机的齿槽转矩峰峰值124.0mN·m，经过上述优化，采用等径磁极、平行充磁、极弧系数为0.925后，齿槽转矩峰峰值只有6.8mN·m，效果非常显著.图11是磁极优化前后4极24槽无刷电机FCU空载仿真曲线.

表3 平行、径向充磁无刷电机的齿槽转矩峰峰值mN·m

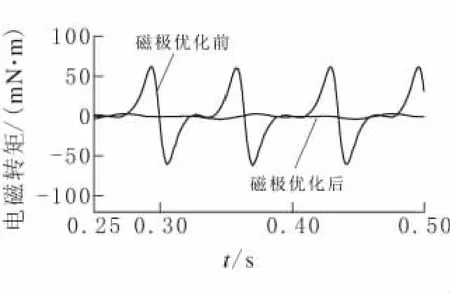
图11 磁极优化前后FCU仿真曲线

3 定子斜槽与转子斜极

定子斜槽或转子分段斜极对无刷电机的转矩脉动也有较好的抑制作用.为了进一步提高晶圆清洗机无刷电机的低速性能，定子斜槽或转子分段斜极也是可以考虑采用的方案.在下面的分析中假定无刷电机定子斜槽时转子为直极，转子分段斜极时定子为直槽.

3.1 定子斜槽

无刷电机定子分别斜槽7.5°（半个齿距）和15°（一个齿距）.为了减小计算量，定子斜槽7.5°、15°均采用4段2－D仿真，然后转矩取平均值.对两种定子斜槽（假定等径磁极、极弧系数为0.925、平行充磁）无刷电机进行齿槽转矩仿真分析，图12是定子斜槽和未斜槽时无刷电机齿槽转矩的仿真曲线.

图12 定子斜槽和未斜槽齿槽转矩仿真曲线

定子未斜槽时无刷电机齿槽转矩的峰峰值为6.8mN·m，定子斜槽15°后齿槽转矩峰峰值为2.94mN·m，比未斜槽时下降131%；定子斜槽7.5°后齿槽转矩峰峰值为2.12mN·m，比未斜槽时下降221%，比斜槽15°时下降39%.可见，对4极24槽无刷电机来讲，定子斜槽7.5°比定子斜槽15°效果更好.

3.2 转子分段斜极

转子斜极有连续斜极和分段斜极两种，如图13所示.连续斜极浪费永磁材料，磁极制作成本较高，较少采用；分段斜极很好地克服了连续斜极的缺点，工程上有一定应用.

图13 无刷电机的转子斜极

转子分段斜极7.5°和15°.采用分段2－D仿真方法，有限元模型与磁极分段数相同，对转子斜极（假定等径磁极、极弧系数为0.925、平行充磁）无刷电机齿槽转矩进行仿真，然后取平均值，仿真结果见表4.图14是转子4段斜极和未斜极齿槽转矩的仿真曲线.

图14 转子斜极和未斜极齿槽转矩的仿真曲线

与定子斜槽一样，转子分段斜极对齿槽转矩平均值没有影响.定子斜槽15°，磁极轴向分5段，齿槽转矩峰峰值最低，但分段数较多，磁极粘贴比较费时；相比而言，斜极7.5°、磁极轴向分3段或4段时的齿槽转矩峰峰值比较低，工艺性好.

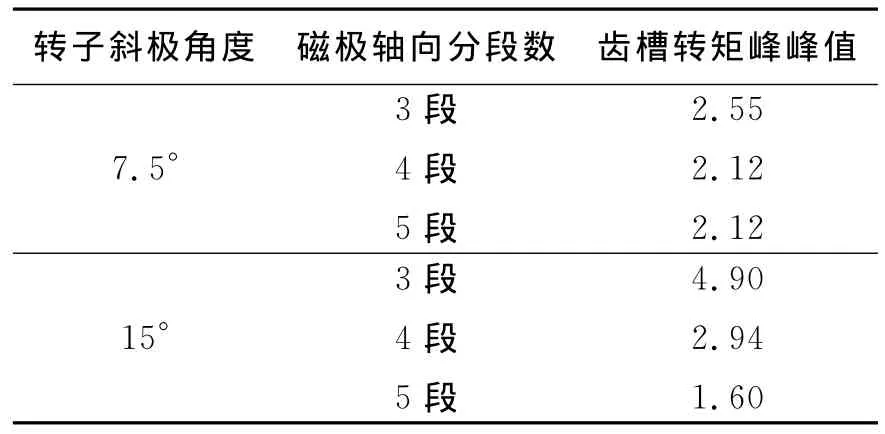
表4 转子分段斜极无刷电机的齿槽转矩仿真结果mN·m

转子4段斜极与定子斜槽齿槽转矩脉动率仿真结果相同，这是因为两者都采用4段二维有限元模型的缘故.定子斜槽和转子分段斜极对齿槽转矩的抑制效果相当，究竟采用哪种方法取决于电机制造工艺方面的考虑.

经过磁极优化，同时采用定子斜槽或转子斜极，无刷电机转矩平稳性得到显著改善。图15、16分别是优化前后，转子4段斜极无刷电机3 000r／min和25r／min时空载转矩仿真波形，采用4段FCU仿真方法，然后取转矩平均值，脉动转矩的峰峰值见表5。优化后高速时无刷电机转矩脉动峰峰值下降了270%，低速时下降2 263%，低速性能改善非常明显.

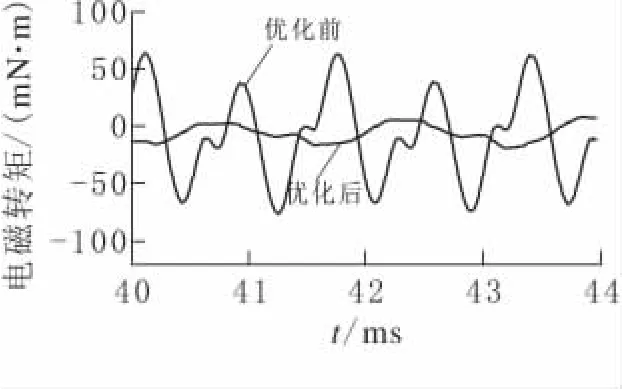
图15 无刷电机3 000r／min时的FCU仿真波形

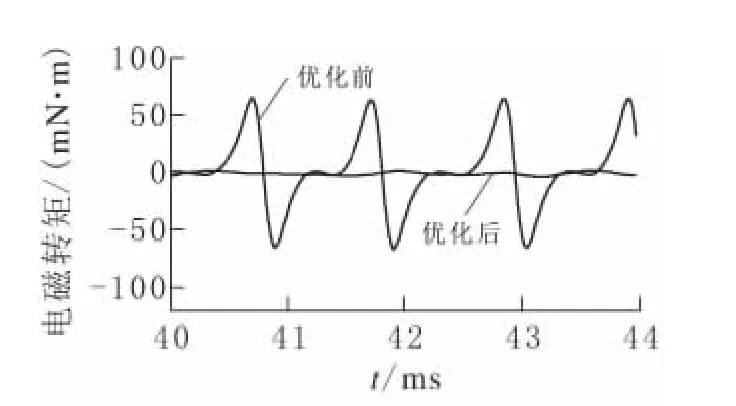
图16 无刷电机25r／min时的FCU仿真波形

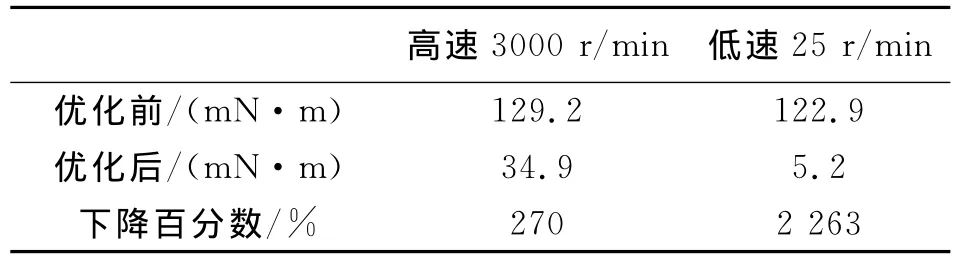
表5 无刷电机优化前后脉动转矩的峰峰值

需要说明的是，上表中脉动转矩的峰峰值包含了由于换相等因素导致的纹波转矩.经过磁极优化、转子4段斜极后，无刷电机的齿槽转矩峰峰值非常低，只有2.12mN·m，但高速3000r／min FCU仿真脉动转矩峰峰值为34.9mN·m，可见现在脉动转矩主要为纹波转矩，需要从控制方面着手加以抑制.

［1］ Wael A.Salah，Dahaman Ishak，Khaleel J.Hammadi，Minimization of torque ripples in BLDC motors due to phase commutation－a review［J］.Przenlad Elektrotechnicany（Electrical Review），2011，87（01）：183－188.

［2］ Thomas M.Jahns，Wen L.Soong，Pulsating torque minimization techniques for permanent magnet AC motor drives－a review［J］.IEEE Transactions on industrial electronics，1996，43（02）：321－330.

［3］ 邹慧明，张立钦，彭国宏，等，基于Simplorer和Max－well联合运行的线性压缩机仿真模拟［J］.压缩机技术，2011（01）：7－11，14.

［4］ 刘长红，杨平西，定子斜槽同步发电机空载电压波形的数值计算［J］.上海交通大学学报，2007，41（11）：1 891－1 895.

［5］ Jabbari A，Shakeri M，Nabavi S A Niaki.Pole shape optimization of permanent magnet synchronous motors using the reduced basis technique［J］.Iranian Journal of Electrical ＆Electronic Engineering，2010，6（01）：48－55.

［责任编校：张岩芳］

Simulation Analysis of Cogging Torque of Brushless DC Motor Used in Wafer Cleaning Machine

LI Xin－hua1，DU Cheng－fei1，HUANG Xian－lei1，YANG Chui－gong2
（1 School of Electrical ＆Electronic Engin.，Hubei Univ.of Tech.，Wuhan 430068，China；2 TPG Motors ＆Drives Co.，Ltd.，Taiwan，China）

The cogging torque results in the low speed performance of brushless DC motors.In this paper，the cogging torque of wafer cleaning machine brushless DC motor was researched by computer simulation，including the influence of the slot／pole combination，skewing slot／skewing magnet pole.On this basis，the optimal design of wafer cleaning brushless DC motor was proposed.

wafer cleaning machine；brushless DC motor；cogging torque；ripple torque；computer simulation

TM351

A

2013－09－13

李新华（1959－），男，湖北武汉人，湖北工业大学教授，研究方向为稀土电机及其控制

1003－4684（2014）01－0007－05