FP标准具的温漂及光学材料光程温度系数的精确测量

朱精敏, 朱旻翔

(1.浙江大学 物理系,浙江 杭州 310027; 2.杭州精诚光电子有限公司,浙江 杭州 310000)

1 引 言

光学玻璃、光学晶体、光纤材料等实际光学材料的有效光程nd的温度系数在某些应用中是重要的参量. 它与光的波长有关，也与所处的基础温度有关，不同厂家不同批号的材料该参量也会有所差别，一些大公司会给出其产品的热膨胀系数αT和在某波长的折射率温度系数dn/dT，但比较粗略，而有些公司的产品则没有这些参量. 在实际应用中，若需该参量的精确值，还得自行具体测试. 采用多光束干涉的FP标准具法来进行这类测量比起传统的用马赫-曾特尔(Mach-Zehnder)干涉仪[1]法能明显提高测量精度，后者受限于条纹读数误差较大，同时样品的加热系统对干涉仪干涉臂长的干扰也会导致增大测量误差.

一般来说，希望FP标准具的温漂率小，以便有更高的热稳定性[2-3]，但适当的温漂也提供了一种有用的调节手段，例如在激光腔内选模中，可用适当的温控FP标准具取代调节FP标准具的倾角，来达到模式的匹配，前者具有更小的损耗和更高的稳定性. 了解温漂率对选用标准具和设计温控系统有参考价值.

2 实验原理

平行平板的干涉公式[4]为

mλ=2ndcosα，

其中，λ为光波长，d为平板厚度，n为平板折射率，α为光束入射角. 当干涉级次m为正整数时，为干涉极大. 为了简化分析，取垂直入射，α=0，则有

mλ=2nd

.

(1)

当nd因温度变化ΔT而改变λ/2时，m改变1，即改变1个干涉级次，即可求得

(2)

若需进一步求得单独折射率的温度系数dn/dT，展开(2)式左边

其中αT是材料的线膨胀系数，可得

(3)

为了提高测量精度可以增大ΔT，使光程nd改变多个λ/2，以减少ΔT的相对误差. (1)式中，若用光频ν代替波长，有

因温度变化ΔT时，n和d都有相应的变化，其m级干涉极大ν的变化为

(4)

(4)式说明，平行平板或FP标准具因温度引起的干涉极大的频漂与平板的厚度d无关，只与平板材料特性和光频有关. 这种频漂对固体FP标准具在用作激光腔内选模[5]时尤为重要. 从(4)式中还可以看到，如果要求FP标准具能有更小的温度频漂Δν，即热稳定性更好，就应选择热膨胀系数αT小，以及折射率温度系数dn/dT小的材料. 空气隙标准具的dn/dT要小得多，一般情况下可忽略. 如有更高要求还可以置于真空室内，使dn/dT为零，同时采用石英玻璃或超低热膨胀玻璃作为间隔器材料.

3 实验方法和结果

对平行平板两表面镀上高反射膜，就构成固体FP标准具SFP. 图1是实验装置示意图，实验装置实物如图2所示. 当温度逐渐变化时，探测到的透射光强如图3所示.

图1 固体FP标准具SFP

图2 实验装置照片

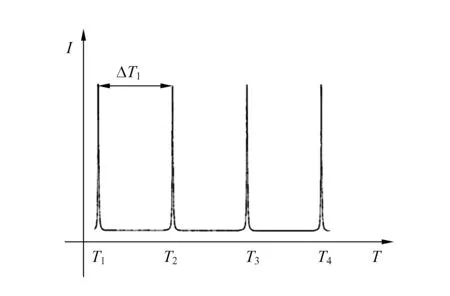
图3 透射光强随温度变化曲线

根据相邻透射峰的温度差ΔT，从(1)式即可得到样品光程的温度系数，若已知材料的热膨胀系数αT，从(2)式可得材料折射率的温度系数. 测定较大αT，现成仪器已很多，文献[6]介绍置于真空室的空气隙FP标准具测定热膨胀系数很小的材料的αT，把待测材料做成空气隙FP标准具的间隔圈，这相当于(3)式左边为0，可直接求得αT.

采用He-Ne激光进行测量，波长为λ=632.8 nm，查得用于制作固体FP标准具的上海新沪玻璃厂的JGS1石英玻璃在标准状况该波长的折射率为n=1.457 2，采用的固体标准具的厚度为d=10.008 mm，其自由光谱范围为：FSR=c/2nd=10.278 GHz.

按(2)式即可算得

误差主要来自温度测量的误差. 各种手册列出的石英玻璃的线膨胀系数αT有所不一，所标相对误差范围也较大，取粗略值αT=5×10-7℃-1(如有必要，可按文献[6]类似方法精确测定所用材料在实际温度的αT值，以确保更高精度.)可按(3)式算得

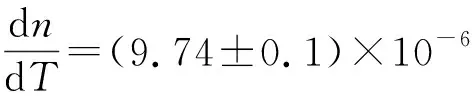
这与康宁公司给出的数值dn/dT=(10±1)×10-6℃-1接近,但有更高的精度和更确切的测试条件. 从以上结果可以看出，对于石英玻璃来说，光程nd的热变化主要来自折射率n的热变化.

把αT和dn/dT代入(4)式，取ΔT=1 ℃，可得温度每变化1 ℃时，任意厚度的该材料制成的平行平板或固体FP标准具极大峰的频漂率为

Δν=-7.184×10-6ν℃-1，

对于He-Ne激光，ν=4.738×1014Hz，其每度频漂率为：Δν=3.403 GHz/℃.

当利用FP标准具作为激光腔内选模器件时，此频漂率的大小对于设计温控器的精度和温度范围来说是重要的参量.

4 讨 论

1)实验能够比较精确地测定光学材料光程nd的温度系数，配合精确测定线膨胀系数的设备，可精确测定材料的折射率温度系数dn/dT.

2)本实验给出了石英固体FP标准具的温漂率，对于固体FP标准具的温度扫描和温控要求可给出有价值的参考数据.

3)本实验实际上是FP标准具在微小长度测量的一种变型应用. 本文虽未涉及材料线膨胀系数的测量，但从上也可以看出，采用FP标准具原理也是这类测量的一种分辨率和精确度特别高的方法.

4)本实验装置简单，但样品制作要求精度较高，平行度需达1.5″以下.

5)为得到较高精度，采用分辨率和准确度较高的温度计是重要的. 同时温度变化过程应非常缓慢，应是准热平衡过程.

参考文献：

[1] 母国光，战元龄. 光学[M]. 北京：人民教育出版社，1978：248-250.

[2] 朱精敏. 塞曼效应实验中F-P标准具的选择和使用[J]. 物理实验，2001,21(特刊)：62-64.

[3] 朱精敏，陈星，周小风. 塞曼效应实验系统评述[J]. 物理实验，2004,24(12):3-6.

[4] 玻恩M，沃尔夫E. 光学原理(上册)[M]. 北京：科学出版社,1978:421-445.

[6] Plummer W A,Hagy H E. Precison thermal expansion measurements on low expansion optical materials [J]. Applied Optics,1968,7(5):825-831.