第2届全国大学生物理实验竞赛试题的解答与考试评析

张宪锋,陶小平,祝 魏,张增明,孙腊珍

(中国科学技术大学 物理实验教学中心，安徽 合肥 230026)

1 引 言

教育部高教司(高教司函[2010]13号)批准的《全国大学生物理实验竞赛》是大学生的学科竞赛，由高等学校国家级实验教学示范中心联席会主办，全国高校实验物理教学研究会协办，中国科学技术大学承办的第2届全国大学生物理实验竞赛于2012年12月22日至12月24日在中国科学技术大学物理学院物理实验教学中心举行. 竞赛旨在培养大学生的创新能力、实践能力和团队协作意识，激发大学生对物理实验的兴趣与潜能，促进大学物理实验教学改革. 来自国家级物理实验示范中心所在院校、国家级基础科学人才培养基地院校及获得国家级物理实验精品课程院校的46个代表队的182名大学生选手参加了本次竞赛. 竞赛命题分为基础性物理实验和综合性、研究性物理实验题2类. 本次实验竞赛既突出物理基础又充分体现大学生的实践能力、动手能力和创新思维. 各代表队由2人分别单独参加4 h的基础性物理实验竞赛；2人合作参加8 h的综合性、研究性物理实验竞赛. 经评审专家组的评审和竞赛组委会审议，评选一等奖12名(其中：基础性试题8名，综合性、研究性试题4名)；二等奖31名(其中：基础性试题20名，综合性、研究性试题11名)，三等奖46名(其中：基础性试题31名，综合性、研究性试题15名).

中国科学技术大学物理实验教学中心承担了本届竞赛的组织、命题、实验仪器装置的研制和实验场地的准备等工作. 本文就第2届全国大学生物理实验竞赛试题的实验内容、考试结果及竞赛中存在的问题做一些分析，希望对促进各高校进一步加强学生实践能力的培养，促进物理实验教学改革提供点有益的借鉴.

2 基础性试题的解答与评析

基础性实验试题为“利用转动定律测量质量及切变模量”和“测量康铜丝的杨氏模量和泊松比”2道题，均使用自己实验台上的装置独自来完成，每道题时限4 h.

2.1 试题1：利用转动定律测量质量及切变模量

2.1.1 引言

刚体绕固定轴的转动定律是研究刚体运动的基本定律，通过对小角度下刚体定轴转动是简谐振动的特性研究，可以确定待测物体的质量.

在弹性限度内，钢丝的切应力τ与切应变γ成正比，即τ=Gγ(其中G为材料的切变模量). 如在钢丝的下端悬挂一圆盘，它可绕中心线往复运动，形成扭摆. 该扭摆扭过的角度φ正比于钢丝所受的扭力矩M，由转动定律可得该扭摆作简谐振动，由此可确定钢丝的切变模量.

2.1.2 实验研究的问题

本实验研究的问题：

1)测量玻璃棒的质量和螺帽的质量；

2)测量钢丝的切变模量.

2.1.3 实验仪器

1)测量玻璃棒的质量和螺帽的质量的器材：长约1 m的木条(过质心附近有一直径约10 mm的小孔，内有套管，套管内径约为6 mm)，质量均匀分布的待测玻璃棒1根(长为L、质量为m1)，待测螺帽2个(总质量为m2)，单摆架1个(上端固定1根直径约4 mm铁杆)，质量m为(15.00±0.05) g、半径为r0的小铜柱2个，秒表1块，游标卡尺1把，直尺1把，平衡刀口1个，坐标纸1张，小剪刀1把，铅笔、蓝彩笔、橡皮和胶带.

2)测量钢丝切变模量的器材：圆盘1个，待测金属丝1根，单摆架1个，游标卡尺1把，螺旋测微计1个，秒表1块，质量m为(50.0 ± 0.1) g、半径为r0的大铜柱2个.

2.1.4 实验要求

第1小题：测量玻璃棒的质量和螺帽的质量(60分)

1)说明如何操作使转轴通过质心，并完成答题纸上的问题.

2)设计实验方案测量玻璃棒的质量和两螺帽(可视为质点)的质量，并给出必要的计算公式. (重力加速度g=9.795 m/s2)(可请求提示设计方案，扣12分)

3)记录6组数据，要求时间测量误差在0.5%以内(人用秒表计时的测量误差为0.2 s),并用作图法确定通过木条质心且垂直其表面的转轴的转动惯量IC.

4)确定玻璃棒的质量m1和两螺帽的质量m2. (不要求计算不确定度)

第2小题：测量钢丝的切变模量(40分)

1)完成答题纸上如何确定钢丝长度的问题.

2)设计实验方案测量钢丝的切变模量，并给出必要的计算公式，要求钢丝的长度约为60 cm，时间测量误差在0.5%以内(人用秒表计时的测量误差为0.2 s). (可请求提示设计方案，扣12分)

3)记录6组实验数据，用最小二乘法拟合计算切变模量. (不要求计算不确定度)

2.1.5 试题特点及解答

1)试题特点

作为基础性实验试题，在定题过程中，出题者经反复讨论和修改，要求试题既突出物理基础理论又充分考查考生的实践动手能力. 第1小题“测量玻璃棒的质量和螺帽的质量”，考查了考生对刚体模型、质心及转动惯量等物理概念的理解；实验中要求考生利用刚体定轴转动定律设计实验方案，测量玻璃棒的质量和两螺帽(可视为质点)的质量，并给出必要计算公式. 第2小题“测量钢丝的切变模量”，考查了钢丝切变模量的基础概念，要求考生采用常规实验器材设计实验方案测量钢丝的切变模量，并给出必要计算公式.

试题难度不大，实验内容及数据的处理量适中，但这2个小题均要求设计实验方案，考生要在4 h内完成实验要求，对考生基础理论的理解程度、基本物理仪器的熟练使用程度以及基本实验技能的储备都是不小的挑战，笔者认为，该试题较全面地考查了考生的基本知识、基本实验技能及数据处理和分析能力，符合基础性实验试题要求.

2)试题解答

第1小题解答：回答答题纸上关于通过配重，使转轴通过木条质心的问题，设计实验方案确定通过木条质心且垂直其表面的转动惯量，测量玻璃棒的质量和螺帽的质量，并给出相关计算公式：

(1)

(2)

(3)

测量并通过作图确定通过木条质心且垂直其表面的转轴的转动惯量(图1)，测量出玻璃棒的质量m1和螺帽的质量m2. (详解略)

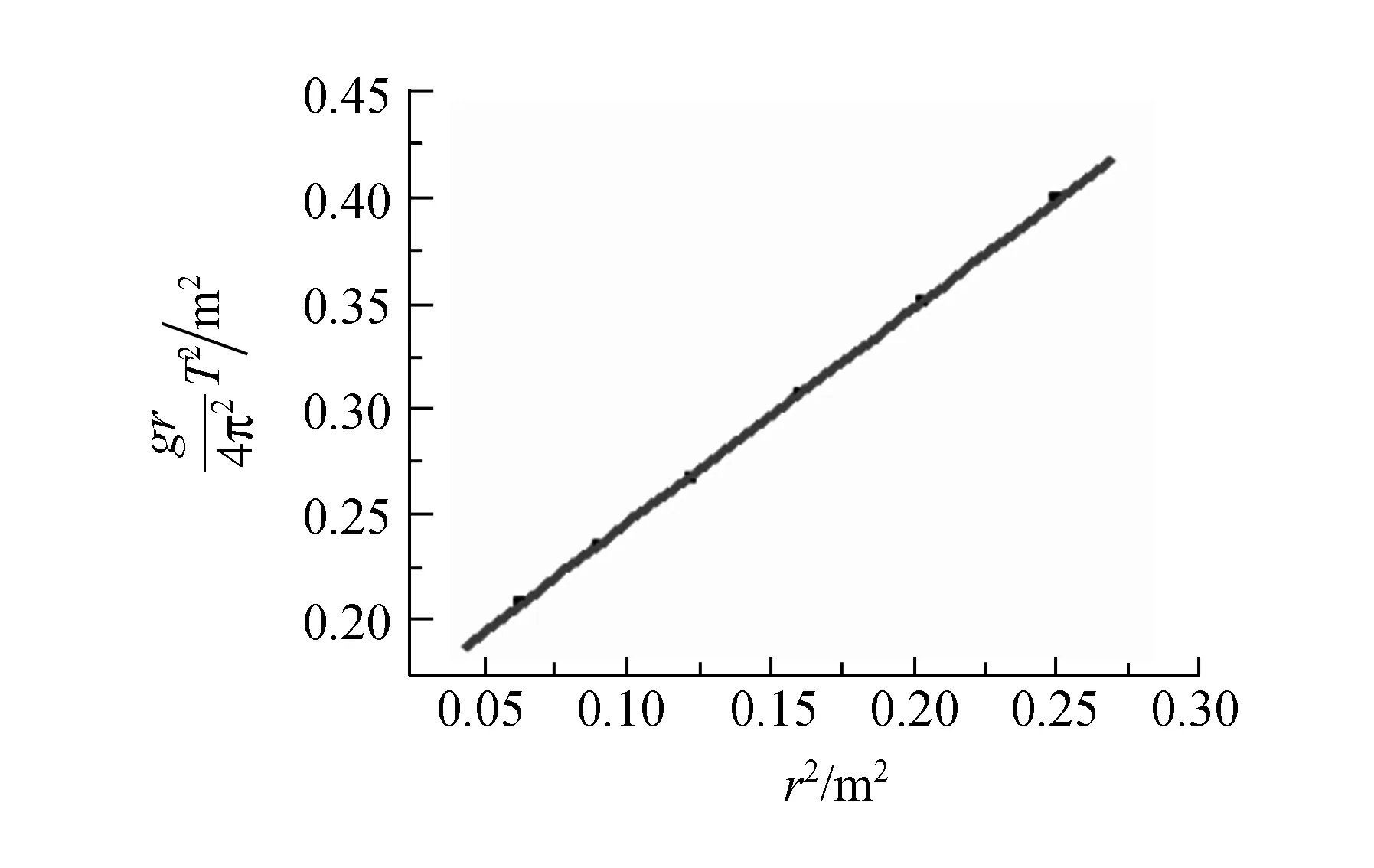
图1 确定通过木条质心且垂直其表面的 转轴的转动惯量

第2小题解答：确定待测钢丝的长度，利用提供的仪器和设备，设计实验方案并且给出相关的计算公式：

(4)

(5)

(6)

通过最小二乘法拟合计算钢丝的切变模量. (详解略)

2.1.6 考试结果及评析

表1是对46名参赛学生基础性实验试题1的得分所作的统计.

表1 统计结果

为便于专家客观评阅试卷，命题组对实验的评分反复进行讨论并细化，关于实验方案的设计、测量结果的计算和分析，在评分细则中都给出了详尽的得分点. 根据最终的统计结果，参赛学生在该试题的各小题及总分得分情况如图2所示(横坐标表示分数的区间，纵坐标表示学生人数)，由图2可以看出，第1小题考生得分普遍很低，有15位考生请求提示设计方案，这部分考生的总分需扣12分，另有部分考生在实验过程中未能正确地设计实验方案，以致实验测量结果和数据处理与参考答案不符，或部分考生因为时间关系没有完成实验，导致得分情况偏离高斯分布. 第2小题得分情况大致符合高斯分布，大部分考生完成了实验，其中有5位考生请求提示设计方案，这部分考生的总分也需扣12分. 值得一提的是，获得一等奖的4位同学无一请求提示设计方案. 总体上看，得分情况大致符合高斯分布，两小题有一定的区分度.

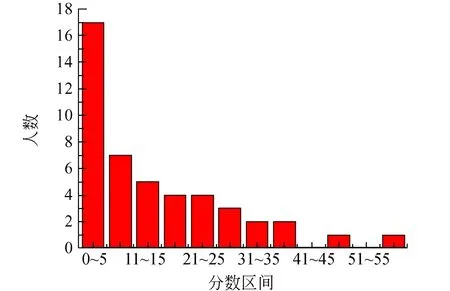
(a) 测量玻璃棒质量和螺帽质量得分分布图

(b) 测量钢丝切变模量得分分布图

(c) 基础性试题1 总分的直方统计图图2 基础性试题各小题及总分的得分情况

通过具体的统计分析，我们分析如下：

1)第1小题突出了实验的基础理论性，涉及基本物理概念和测量技术. 从监考和阅卷中可以看出，有近1/3的考生拿到题目后无从下手，没有根据实验提供的器材正确地设计实验，得分很少. 有15位考生请求了提示设计方案，这部分考生基本完成了实验，但总分需扣12分. 部分考生对刚体质心的概念、刚体定轴转动定律及简谐振动性质等基本知识理解不够，未能按要求用作图法确定出通过木条质心且垂直其表面的转轴的转动惯量，导致后续实验无法完成. 有些考生缺乏基本的实验技能，不能有效地使用提供的实验器材，导致实验方法错误. 本小题的平均得分为14.30分(满分为60分)，得分为0分的有7人. 综合看来，第1小题是对考生的基础理论和实验技术的较全面考察，大约有30%的考生完成了此实验.

2)第2小题要求考生先设计实验方案，并给出测量钢丝的切变模量的计算公式. 从监考和阅卷中可以看出，部分考生由于审题不全面或不仔细，没有根据实验提供的器材正确地设计实验. 圆盘和2个大铜柱是本实验提供的主要器材，近30%考生出现测量错误，反映出考生实验技术水平有待提高. 当然，还有相当部分的考生由于缺乏参赛经验，时间分配不够合理而未完成答卷，所有这些导致考生得分普遍很低. 从统计情况看，本小题的平均得分为11.55分(满分为40分)，得分为0分的有5人. 综合看来，第2小题是对考生基本实验技能和实验数据处理能力的考察，大约40%的考生基本完成了此实验.

3)总之，试题1强调了实验的基础理论和测量技术，对实验的基本技能、实验数据处理和作图等都有较高的要求，参赛考生的最高分96分，最低分0分，平均分25.85分，考试成绩基本符合统计高斯分布.

2.2 试题2：测量金属丝的杨氏模量和泊松比

2.2.1 引言

杨氏模量是材料的重要力学性质，反映了材料抵抗形变能力的大小. 拉力F与丝的原始横截面A之比定义为应力，伸长量ΔL与丝的原始长度L之比定义为纵向线应变. 在弹性范围内，应力与应变满足胡克定律：

(7)

其中E为材料的杨氏模量. 式(7)中只考虑了材料的微小纵向应变，忽略了横向变化. 横向伸长量Δd与丝的原始横向长度d之比定义为横向线应变. 在实践中，纵向拉伸应变还会导致横向收缩应变. 实验表明，在材料弹性范围内，横向线应变Δd/d与纵向线应变ΔL/L之比为常量：

(8)

(8)式中的负号表示纵向拉伸导致横向收缩，μ为横向变形系数或称泊松比.

非平衡电桥与传感器配合使用，可测量温度、应力、位移等变化量. 图3为非平衡电桥的原理图，其中电阻箱R1，R2，R3为电桥的3个臂，R4+RS构成第4臂，R0为电位器，C是滑动头. 当电桥平衡时：

图3 非平衡电桥

任意桥臂阻值变化时，电桥将偏离平衡位置. 实验中，金属丝受到拉伸引起电阻变化，当R4+RS的相对阻值变化量小于1%时，桥电压Ug(即DE间电压)与电阻的关系近似满足线性关系：

(9)

式中，RS是康铜丝的初始阻值.

2.2.2 研究的问题

1)测量康铜丝的杨氏模量；

2)忽略拉伸过程中康铜丝的电阻率变化，利用非平衡电桥测量拉力与康铜丝有关性质的关系，并计算其泊松比.

2.2.3 实验仪器

所用的实验仪如表2所示.

表2 实验仪器

2.2.4 实验要求

1)按图3连接电路，建议分压UAC取0.3～0.5 V，康铜丝的工作电流取3～5 mA.

2)托盘上放1块砝码作为初始条件，调整仪器两端的塑料螺栓，使康铜丝与桌面平行，距离桌面77 mm左右，以利于移测显微镜的调节.

3)测量康铜丝接入电路的长度L，精确到mm.(7分)

4)用干涉法测量康铜丝的直径d.(30分)

a.简述干涉条纹在整个劈尖区域分布特点并解释；为提高测量精度，应测什么区域的条纹？

b.用干涉法测量康铜丝的直径(选一处即可)，要求测量相对不确定度小于1.0%，并给出测量依据.

5) 分别朝康铜丝上的2个焊接点哈气，并观察桥电压Ug的读数变化.(10分)

a.描述哈气时读数的变化；

b.上述现象由什么效应产生？

6)测量康铜丝的杨氏模量E.(25分)

a.设计实验方案，给出相关公式；

b.求康铜丝的杨氏模量E(合肥地区重力加速度g=9.795 m/s2).

7)确定康铜丝的泊松比μ(28分)

a.设计实验方案，给出相关公式，忽略拉力对金属丝电阻率的影响；

b.确定康铜丝的泊松比μ.

2.2.5 试题特点、解答及评析

1)试题特点

本题原理部分比较简单，所用实验设备都是常见的设备. 主要考查内容包括：由不确定度分析设计实验方案，用干涉法测量康铜丝的直径，拉伸法测量康铜丝的杨氏模量，非平衡电桥法测量康铜丝的泊松比，此外还要求学生解释实验中2个比较有趣的实验现象. 竞赛组委会的专家在审核命题过程中认为，本实验的几个内容单独看比较简单，很多高校都开设了相关的实验，但将这几个涉及力学、热学、电学、光学等学科的基础实验综合在一起，对学生基本物理理论的理解水平、动手能力、分析问题的能力、数据处理的能力要求较高，能实实在在地检验学生的物理实验水平.

2)试题解答

第1小题要求学生连接非平衡电桥的电路，第2小题调节康铜丝水平，都是非常基本的操作，难度很小.

第3小题要求用卷尺测量接入电路的康铜丝长度L，如图4所示. 由于L大于1.2 m，单个考生直接测量L将导致较大的误差，不能满足精确到mm的要求，只能先测出L1和L2，再求出L. 在实际操作中，只有3人能正确完成本小题，大部分学生直接测量L，说明没有认真审题，动手时对不确定度的大小没有仔细考虑，考试中学生动手不动脑的问题普遍存在.

图4 支架上的康铜丝

第4小题用劈尖干涉法测量康铜丝的直径. 要求先用移测显微镜观察条纹的分布特点并解释，再用不确定度均分原理设计实验方案，并根据实验方案测量直径d. 由于康铜丝比较粗，移动显微镜时，在劈尖区域有的地方有干涉条纹，有的地方没有条纹，这个现象可用钠黄光具有双线波长来解释. 原理如图5所示. 根据不确定度均分原理，可推导出至少需要测量50个条纹才能满足设计要求.

图5 干涉法测细丝直径

本小题考查的不确定度均分原理是物理实验的基础知识，干涉法测细丝直径实验在很多高校都有开设. 但从考试结果来看，74%的考生不能正确推导出干涉法测细丝直径的公式，余下的考生中，只有2人能根据不确定度均分原理进行实验方案的设计. 由于本题的实验现象不常见，操作时，80%的考生超过1 h也没有调出干涉条纹，看到条纹的同学均未能用钠黄光双线波长对实验现象进行解释. 这说明部分考生对物理实验的基础知识掌握不够扎实，对劈尖干涉法的理解不够深入. 这部分的成绩统计见图6.

图6 第4小题成绩分布

第5小题，当考生对着康铜丝的一端焊点哈气时，会发现电桥的平衡示数增大，朝另一端哈气则示数减小，这可用温差效应来解释. 经统计，有28人发现哈气对桥电压的影响，但只有7人正确解释了实验现象.

第6和7小题要求先设计实验方案，再测量康铜丝的杨氏模量、泊松比. 根据式(7)，测出康铜丝的直径d后，用拉伸法很容易测量杨氏模量. 式(8)中，康铜丝直径的变化Δd很小，本实验不能直接测量，但由于Δd会引起康铜丝电阻的变化，因此可通过非平衡电桥测出其阻值的变化间接测量Δd，从而求得泊松比. 相关实验结果见图7和图8.

图7 拉伸法测量康铜丝的杨氏模量

图8 非平衡电桥法测康铜丝的泊松比

最后两小题对考生分析问题、解决问题的能力要求较高. 其难点在于实验设计部分，大部分考生没有清晰的思路，也没有想到移测显微镜除了用来测细丝直径，还能用于监测康铜丝的伸长量. 因此，考生的成绩基本来自于对杨氏模量、泊松比的公式推导及用非平衡电桥测电阻的变化，而无人正确测出这2个物理量. 这两小题总共53分，得分大于10分的有15人，但只有2人成绩超过25分.

46位参赛学生的成绩统计如图9所示，成绩普遍不理想，但基本符合高斯分布. 本实验除了要求灵活使用常见的实验仪器之外，设计性内容较多，还要求学生对实验现象进行分析，并给出相应的理论解释或者测出实验数据. 考试的结果表明大部分考生分析问题、解决问题的能力较弱，这警示在以后的物理实验教学中，应减少教师示范、学生依样画葫芦的教学模式，加强了对学生自主设计性实验的训练，切实提高了他们的实验动手能力.

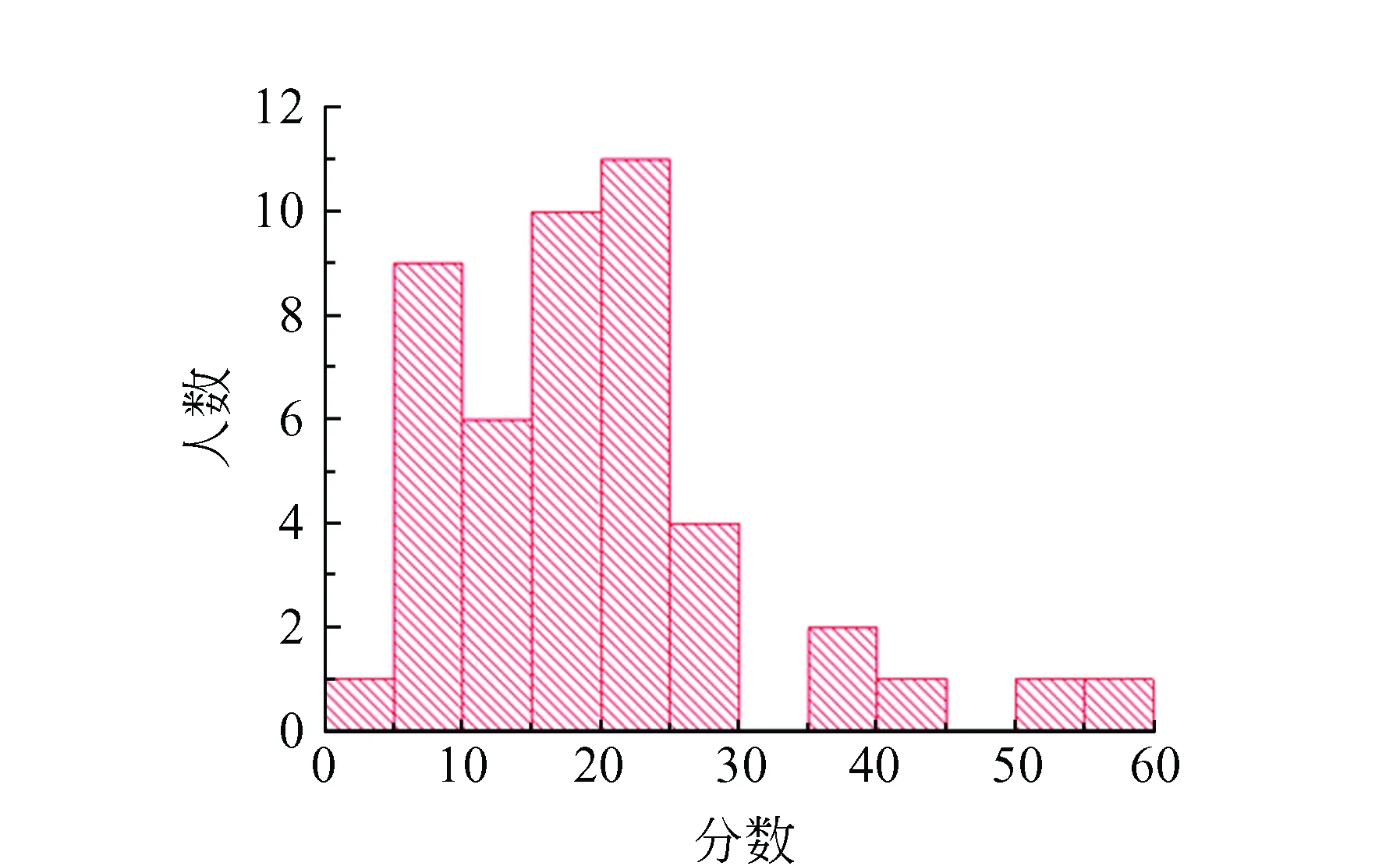
图9 基础第2题考生成绩统计图