定量评估DCS的可靠性

杨刚

(中国石化工程建设有限公司，北京 100011)

近年来，随着国家防灾减灾要求和意识的提高，人们对包括石油化工工业在内的各行各业安全生产的重视程度越来越高，对控制系统长周期安全运行的要求也越来越高。在自控仪表的设计过程中，需要对几种不同的设计方案进行经济性和可靠性评估。与可靠性相关的参数有很多，如可靠度、可用率、失效率、平均失效时间(MTTF)、诊断覆盖率等。由于评估方法的可变性、多样性和不精确性等因素的影响，使得怎样结合这些参数对控制系统的可靠性进行定性、定量分析，如何选用较为经济的方案获得相对大的安全系数，成为控制系统设计过程中的一大难题。文中通过对分散型控制系统(DCS)性能指标的分析，结合石油化工行业DCS常见的应用案例，介绍定量评估DCS可靠性的方法。

1 功能安全要求

安全是人们所追逐的目标，但只是个相对的概念。绝对安全状态是不存在的，在各个状态中，相对引起损失最小的状态即为安全状态。安全停车相对于危险运行是安全状态，非计划停车相对于正常运行就是非安全状态。因此，安全仪表系统(SIS)与DCS对安全的要求有很大不同。

SIS必须保证系统在故障状态下是安全的，虽然可用性也很重要，但安全性的要求始终是第一位的;而DCS强调可用性，即强调任何时候都能正常工作的概率。虽然失效模式(安全失效或者危险失效)也是必须要考虑的因素，但为了减少非计划停车，保证长周期正常运行，可用性的要求是第一位的[1]。因此，DCS可靠与否，通常包括两个方面：产品在规定时间内，完成规定功能的能力，即可使用性；故障发生后通过维修使系统恢复工作的能力，即可维修性。这两种能力统称为可靠性[2]。

2 可靠性参数

2.1 可靠度

可靠度是指系统在设计技术规范内，单位时间内能够完成预定功能的概率。该定义包含了预定功能和时间函数两个重要的概念。设备和系统是否失效，是以其能否完成设计预定的功能来界定的。例如仪表元件的外壳已经严重破损，但只要能准确完成检测和信号传输的功能，就依然可以认为该元件是可靠的。但单纯说系统的可靠度是0.99是没有意义的，这是因为系统中大多数部件的可靠度会随着时间的推移而下降，只有说系统在连续工作了单位时间(例如：1×104h)后的可靠度是0.99才有意义。

对于石油化工行业，仪表设备和系统通常是可维修的，因此不必像航空、航天领域那样追求系统必须可靠地连续工作。相对于可靠度，更常见的参数是平均失效时间(MTTF)和平均修复时间(MTTR)。多数行业，如工业、商业、运输业等，所用的控制系统、设备等的使用寿命比平均失效时间长，缘于可维修、可维护。而航空、航天应用中的某些设备和系统的使用寿命比平均失效时间短，所以常会看到一些需要高可靠性应用的退役设备，还可以在其他应用中正常使用很长时间，这是由各类应用对可靠性的要求不同所致。

2.2 平均失效时间

MTTF是指工作单元失效前正常工作的平均时间，也称平均无故障时间、平均失效前时间。MTTF经常被误认为是产品寿命，实际上它只是产品失效前期望的时间。一个MTTF为2×105h的部件，有可能工作1000h后就发生故障。部件或系统的MTTF数值可以在一定程度上反映产品的可靠性，但不能直观地表述多个部件在运行一段时间后发生故障的概率，也不能确定这台设备或系统的故障时刻。

2.3 平均修复时间

MTTR是指故障修复所需要的平均时间。平均修复时间包括诊断、确认、故障定位、部件获得、修复和测试所需的时间。平均修复时间是系统可用率计算的重要参数。

2.4 可用率

可用率是任何一个时刻，系统正常工作的可能性。假定系统的维修率μ为常数且等于1/MTTR，则可用率A：

A=μ/(λ+μ)=MTTF/(MTTF+MTTR)

(1)

式中：λ——系统的失效率。

与MTTF相似，可用率也是一个容易被误解的参数。对于大多数供货商的DCS模件，MTTF远大于MTTR，因此多数DCS供货商都可以提供很高的可用率指标。例如，1个元件的MTTF为2×105h，MTTR为8h，由式(1)可以算出：A=0.99996。

从结果来看，似乎DCS不需要采用冗余结构就可以达到很高的可用率，但同样用该参数计算失效率，却能得出完全不同的结论。

2.5 失效率

失效率是指正常工作的产品在单位时间内失效的概率，常用的单位为FIT(每109h的失效次数)。用数学公式表达：

λ(t)=单位时间内的失效次数/元件总数

(2)

例如：某炼油厂DCS共有1000个I/O模件，运行5a期间共发生了10次失效，则：

λ(h)=10/(1000×5×8760)=2.283×10-7=228(FIT)

(3)

如果系统部件具有指数衰减规律的失效概率，那么它们的失效率就会为常数，可以认为

λ=1/MTTF

(4)

在单位时间t内发生失效的概率：

P(failure)=1-eλt≈λt

(5)

例如：某炼油厂1套新的DCS共有1000块模件组成，模件平均的MTTF为2×105h，未来连续运行5a期间，DCS模件预计的失效次数为

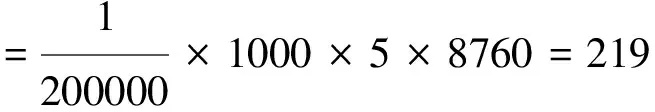
(6)

由此可以看出，如果把MTTF当做产品寿命，很容易会误以为MTTF高达2×105h的模件在运行5a期间不应该或者很少会出现失效，而实际上可能的失效次数却有219次之多，平均每5块模件中至少有1块可能会失效。从这个角度来看，似乎该DCS的可靠性很低。

3 可靠性参数分析

为什么同样1套DCS用不同的参数表述，会得到反差如此大的结论，这是因为DCS是由大量模件组成的复杂串并联系统，用单一部件的参数描述整个系统的可靠性是非常不准确的。以DCS模件为例，单个模件工作2×105h会发生1次失效，而1000个模件工作2×105h总共可能发生1000次失效。同时，所有可靠性参数都与时间有关，系统连续运行的时间越长，发生失效的概率也越大。由式(5)可知，单个模件工作1a失效的概率：P(failure)=(1/200000)×1×8760=0.0438，而连续工作5a失效的概率：P(failure)=(1/200000)×5×8760=0.219。

由此可见，相对于MTTF和可用率，失效率更能准确表达系统的可靠性，对于串并联系统也是如此。

4 串并联系统

非冗余控制系统的回路结构是典型的串联系统，如图1所示，其系统总失效率为

∑λ=λA+λB+λC+λD+λE

(7)

图1 非冗余控制系统回路结构示意

冗余控制系统的回路结构是典型的串并联系统，如图2所示。在理想状态下，模件C，D，E只有一种失效模式，即在2个并联部件同时失效时，系统才会失效，其系统总失效率：

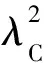
(8)

图2 典型DCS冗余系统回路结构示意

由此可知，对于整个系统而言，串联的级数越多，系统的失效率越高，而采用并联结构可以有效地降低系统的失效率。

5 诊断覆盖率

对于并联系统而言，式(8)是工程上一种最简化的算法，计算是基于所有模件的失效均能被完全地检测到并立即得到维修，而在实际应用中这是不可能的。分析系统的可靠性，必须要考虑到系统的诊断能力和可修复能力。

按照IEC 61508-4的定义，诊断覆盖率C是指发生危险失效时被自动在线检测到的概率[3-4]。用公式表达：

(9)

式中：λDD——检测到的危险失效概率；λD——总的危险失效概率。

以有3种部件组成的系统为例，部件1的失效率为0.098/h，部件2，3的失效率均为0.001/h。假定部件1的失效可以被系统诊断；而部件2，3的失效不能被系统诊断。根据式(9)，系统的诊断覆盖率：C=0.098/(0.098+0.001+0.001)=0.98。

从该例子可以看出，虽然系统只有33%的部件可以被诊断，但由于该部件的失效率远大于其他2个部件，因而系统诊断覆盖率是98%而不是33%。由此可见，诊断覆盖率的大小并不取决于可被诊断的部件数量比例，而是取决于所有失效中可被诊断的比例，这意味着系统诊断应该主要关注那些容易发生失效的部件，而不必覆盖到所有部件。

图3为具有诊断功能的双重冗余控制系统的马尔可夫模型[4]，单个控制器失效率为λ，诊断覆盖率为C，维修率为μ。为了便于说明，这里采用MTTFS描述系统整体的可靠性：

MTTFS=[3λ2+(3-2C)λμ]/[2λ3+2(1-C)λ2μ]

(10)

图3 双重冗余控制系统的马尔可夫模型

假设单个控制器的MTTF为2×105h，MTTR为8h，则λ=5×10-6/h，μ=0.125，系统的MTTFS为

MTTFS=(75003-50000C)/(0.25001-0.25C)

(11)

从式(11)可以算出，对于没有诊断功能的控制系统，即C=0时，冗余系统的MTTFS为3×105h，仅比单控制器增加了50%。而C为99%时，MTTFS则高达1.016×107h。由此可见，C对冗余系统来说是非常重要的指标。双重冗余控制系统MTTFS与C关系曲线如图4所示，可以看出C低于90%时，系统MTTFS随C的提高而增长的幅度非常有限。而C超过95%后每增加1%，系统的MTTFS都会成级数增长。

图4 双重冗余控制系统MTTFS与

6 提高DCS可靠性的措施

DCS的失效分为两种：局部功能失效(安全失效)和整体功能失效(危险失效)。局部功能失效是指由于部件故障，造成DCS无法完成部分功能，但整个系统仍在运行，可以维持生产装置的正常生产。整体功能失效是指DCS无法完成预定的功能，使得生产过程被迫停止。提高DCS可靠性关键在于避免整体功能失效，减少局部功能失效的次数，并尽快从失效状态中恢复。提高DCS可靠性的方法有很多，除了提高元器件MTTF指标，系统对环境的适应性，采用冗余技术等常规措施外，还可以通过可靠性计算对设计方案作进一步优化。

6.1 冗余方案选择

冗余技术是增加系统可靠性最有效也是最常见的方式，对于会引起整体功能失效的关键部件，如控制器、电源、通信模件等，一般均采用冗余技术。但对于串并联系统来说，冗余方式的不同其系统的可靠性也不尽相同。

图5所示的非典型冗余系统结构看起来与图2没有太大差别，但采用简化计算方式可知图5的系统总失效率：

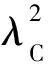
(12)

比较式(12)与式(8)，系统失效率增加了2λCλD+2λCλE+2λDλE，显然图5所示的系统结构可靠性更低。因此，即使对于冗余系统也应进行可靠性分析，评估其方案的合理性。

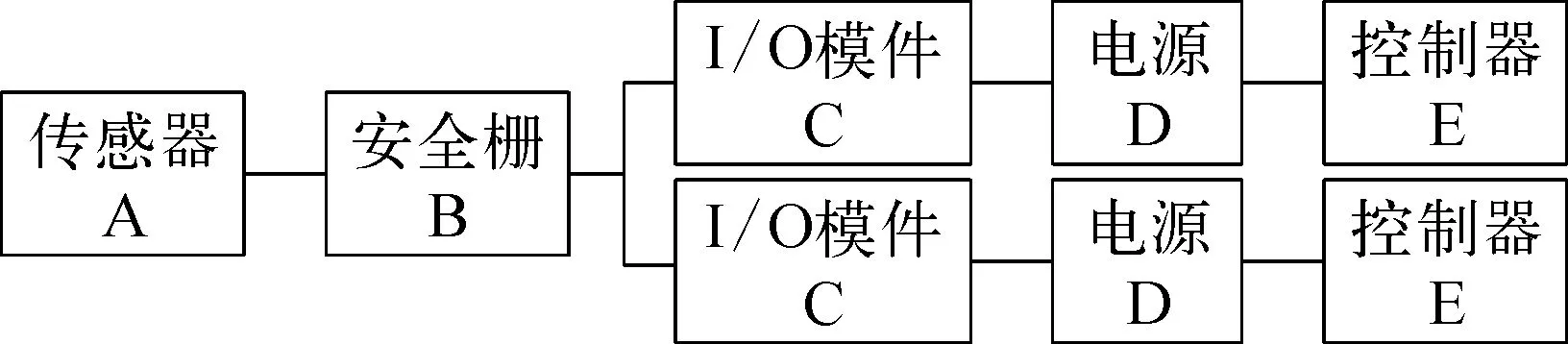
图5 非典型DCS冗余系统结构示意

6.2 简化结构设计

由串并联系统的失效率分析可以看到，设计越复杂的系统可靠性越低，因此在设计过程中应尽量减少信号回路中的传递环节。

以温度控制回路的设计方案为例，由于一些DCS的温度信号输入模件无法做到冗余配置，在设计中会采用在温度控制回路中增加温度变送器的方案，以提高系统的可靠性。

图6为不采用温度变送器的回路结构，其系统总失效率简化计算为

(13)

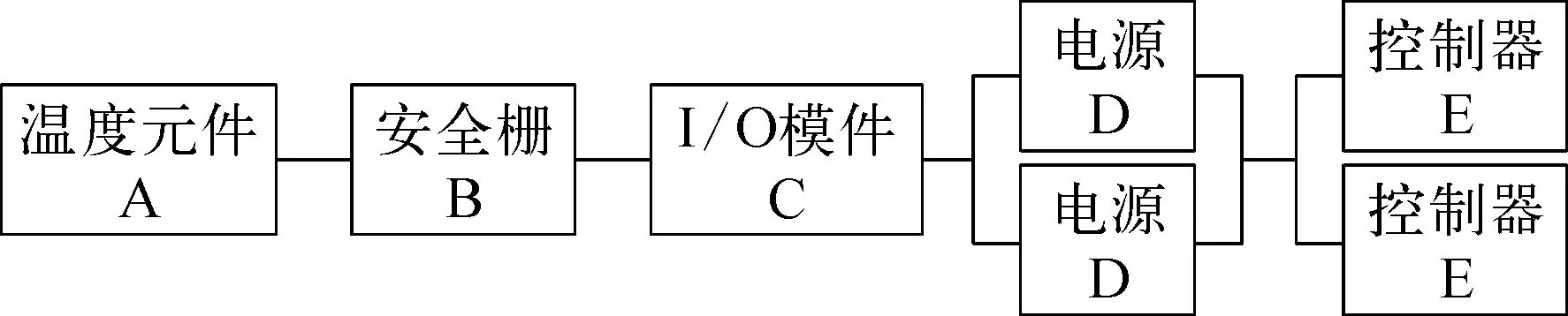
图6 不采用温度变送器的回路结构示意

图7为采用温度变送器的回路结构，虽然I/O模件可以冗余配置，但回路中增加了变送器环节F，其系统总失效率：

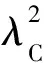
(14)

图7 采用温度变送器的回路结构示意

对比两个系统的失效率：

∑λ1-∑λ2=λC-λF-λC2

(15)

由此可知，只有温度变送器的失效率低于温度I/O模件时，图7所示方案的可靠性才有可能增加。而如果温度变送器的失效率高于或等于温度I/O模件时，图7所示方案不但增加了采购成本，而且系统可靠性也降低了。因此，仅以提高系统可靠性为目的而增加中间环节，往往达不到目的。

实际上对于图6所示的方案，温度控制回路的输入模件如果无法做到冗余配置，可以采用1∶1备用的方式(冷备冗余)。虽然该方式不能减少温度控制回路的失效率，但在故障修复时不需要部件获得时间，因此可以大幅减少系统修复的时间，有效提高了控制回路的可用率。

6.3 定期检修

为了提高系统可靠性，除了增强DCS自身的自动诊断功能外，日常维护中还应采取人工检查措施，以便对失效的部件及时维修、更换。

如图8所示，定期对DCS无法诊断的失效进行检查，可在系统整体失效前进行维修，与图3的模型相比，系统的MTTFS将会进一步增加。

MTTFS=[3λ2+(3-2C)λμ0+(1+2C)λμP+

μ0μP]/[2λ3+2(1-C)λ2μ0+2Cλ2μP]

(16)

图8 定期检测的冗余控制系统马尔可夫模型

依然以第5章的例子来说明，假设每年对DCS全面检修1次，每个控制器维修时间为8h，则μP=1/(8760/2+8)=2.279×10-4，系统的MTTFS为

MTTFS=(1214548.58-49908.84C)/(0.25001-0.2495C)

(17)

从式(17)可以算出，对于没有诊断功能的控制系统C=0时，该系统的MTTFS为4.858×106h，而C为99%时，MTTFS则高达3.805×108h。与式(11)的计算结果对比可知，增加人工检修的频率可以使系统可靠性得到很大提高。

6.4 减少故障修复时间

由于技术水平和加工成本的限制，无限制提高DCS部件的MTTF和C指标是不现实的，为提高系统可用性，还应尽量减少MTTR。大多数DCS供货商提供的MTTR参数一般为4～8h，但该时间的估算往往是建立在用户库房中存有现成备件的基础上，仅包括了部件的诊断、确认、故障定位、修复、测试时间，而没有包括部件的获得时间。如果部件发生失效，用户却没有可维修的手段或可更换的部件，而供货商又无法快速提供服务时，MTTR就会大幅加长。有时部件的订购、制造周期长达数周，这样系统的可用率就会大幅降低。但采购过多的备件，不仅会造成一次性投资过高，而且给设备管理和存储带来困难。比较科学的方法是：通过DCS部件的MTTF参数计算未来几年内的各个部件的可能失效次数，再根据部件的采购周期合理安排备件的种类和数量。

还是以2.5节的例子来说明，1000块模件组成的DCS连续运行5a约发生219次失效，如果每次失效均需要更换模件，且每2a采购1次备件，那么，失效次数=(1/200000)×1000×2×8760≈88。因此，第一次采购10%的备件就足够了。如果系统已经运行了2a，在以后的3a中总共需要多少备件？

假设系统运行的前2a间发生了88次失效，均已更换了新的模件，那么未更换的912块模件未来3a发生失效的次数为131次。已更换的88块模件未来3a失效次数均为12。因此，未来3a模件总失效次数约为131+12=143次。考虑到运行前2a发生的88次失效不会都是发生在运行的第2年末，失效次数实际还会更大一些，因此未来3a备件的需求数量约为150块。

失效率的计算方法有两种：根据供货商提供的MTTF参数计算的理论失效率(见式(4))；根据实际发生的失效次数统计出来的统计失效率(见式(2))。一般来说，统计失效率的准确度要高于理论失效率，但前提是统计的时间和元件数量函数要足够大，因此用户可根据实际情况选择计算的方法。系统连续运行的时间越长，需要备件的数量就会越多。如果炼油厂DCS维护人员水平较高，不必每次失效都更换新的模件，那么系统所需的备件数量可以相应减少。

7 结束语

很多有经验的系统工程师对DCS的可靠性定量分析往往持怀疑态度，这是因为定量分析的数据来源不够准确。另外，概率论和统计学的分析方法在结果方面的不确定性，也会使得评估结果与系统实际数据不一致。但定量分析方法无疑具有巨大的实用价值，可以纠正定性分析中错觉造成的偏差，帮助用户和设计人员作出更加经济、可靠的方案。现实应用中，可靠性的定性评估依然十分重要，定性评估不仅可以防止不准确的数据进入定量评估过程，还可以减少定量评估对数据来源准确度的依赖。

参考文献：

[1]中国石化工程建设有限公司. GB/T50770—2013石油化工安全仪表系统设计规范[S]. 北京：中国计划出版社，2013：3.

[2]WILLIAM M G. 控制系统的安全评估与可靠性[M].白焰，董玲，杨国田，译.北京：中国电力出版社，2008：170.

[3]刘翠岭，黄建兵. 集散控制系统[M]. 北京：中国林业出版社，2006：179.

[4]International Electrotechnical Commission. IEC 61508—2010 Functional Safety of Electrical/Electronic/Programmable Electronic Safety-Related Systems [S]. International Electrotechnical Commission，2010：29.

[5]张建国.安全仪表系统在过程工业中的应用[M].北京：中国电力出版社，2010：241.