实际气体的流量补偿

缪玲梅，李珍华

(华东理工大学 工程设计研究院，上海 200237)

在工程应用中对实际气体的流量补偿往往仅用温度和压力补偿，对实际气体流量进行修正。由于实际气体与理想气体的偏差，仅用温度、压力补偿会造成实际气体流量计量的偏差。李-凯斯勒(Lee-Kesler)方程是对应状态法中计算压缩因子最好的方法。但因查表使精度下降，且计算方法困难。因此，目前对实际气体仍未采用压缩因子补偿。文中介绍用PLC功能块图中的反馈变量作为迭代变量，实现压缩因子计算，解决了实际气体流量的压缩因子补偿问题。

1 理想气体的温压补偿

当被测理想气体温度和压力波动时，为获得质量流量，可采用下列数学模型计算差压Δp。

(1)

式中：下标1——工作状态；下标n——标准状态；p——表压；t——摄氏温度。

2 实际气体的压缩因子

由于实际气体不是理想气体，因此，用压缩因子Z描述其与理想气体之间的偏离程度。即：

(2)

实际气体因存在分子间的引力及分子具有一定体积，因此，具有可压缩性。在对比状态下气体压缩因子与对比参数的关系如图1所示。

由于物质在临界状态时具有相似性，因此，可用临界性质作为对比基础的状态方程。

1975年，李(Lee B I)和凯斯勒(Kesler M G)改进皮策(Pitzer)的研究结果，采用下列Lee-Kesler(李-凯斯勒)方程，将压缩因子表示为

(3)

式中：ω——偏心因子；上标(0)——简单流体(例如甲烷、氩和氪)；上标(r)——参考流体(正辛烷)。参考流体正辛烷的偏心因子ω(r)=0.3978，并用表格形式提供对比温度在0.3～4.0，对比压力在0.01～10.00时与压缩因子和热力学性能之间的关系。

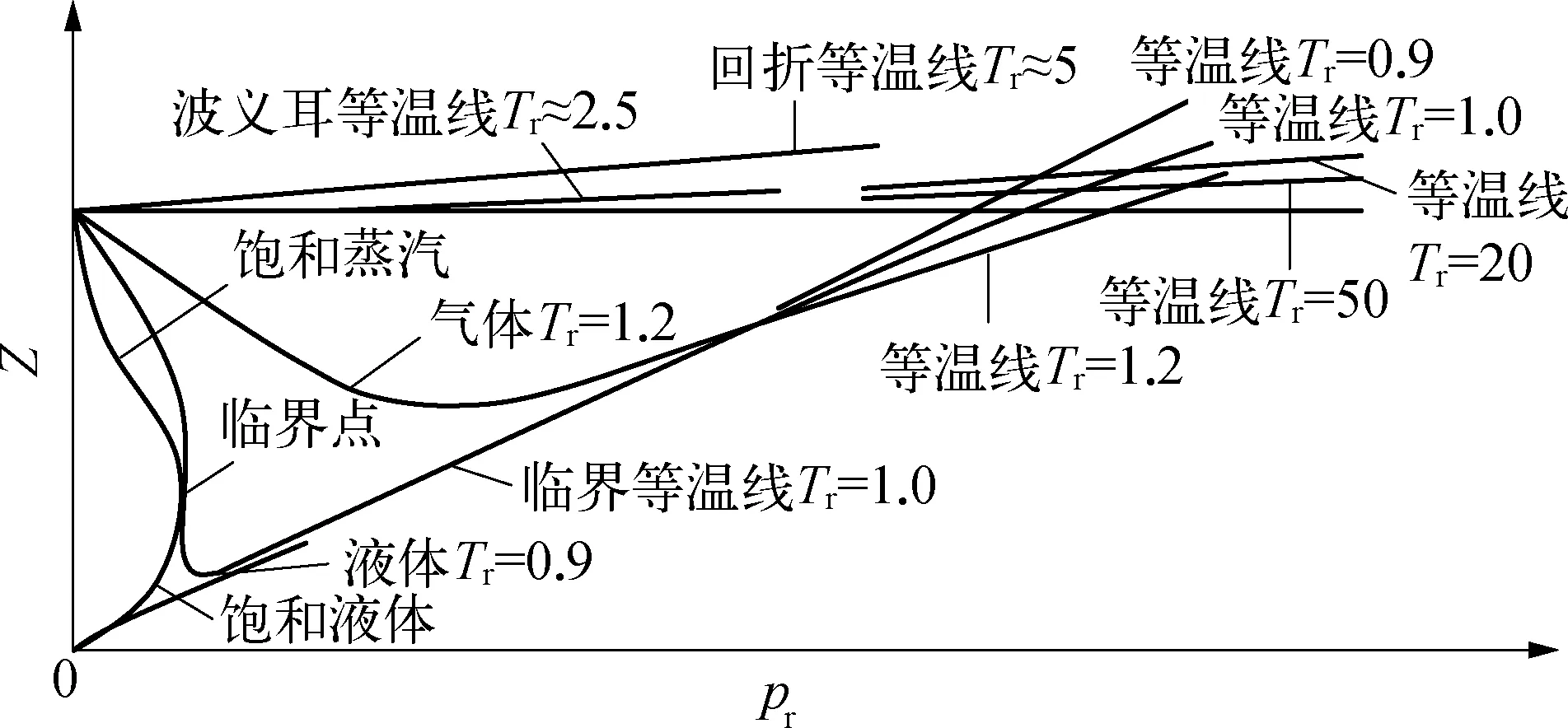
图1 气体压缩因子(Z)与对比温度(Tr)、对比压力(pr)的关系示意

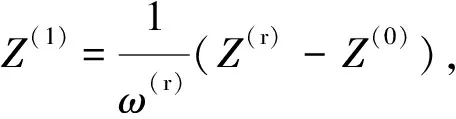
Z(0)和Z(1)可根据维里方程确定。即：

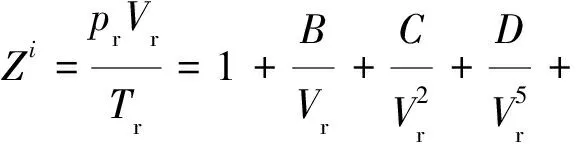
(4)

根据维里方程可确定简单流体和参考流体在对比温度和对比压力下的Zi(i=0， 1)。再根据被测流体的ω可计算Z。表2是常见实际气体的临界温度、临界压力和偏心因子的数据。

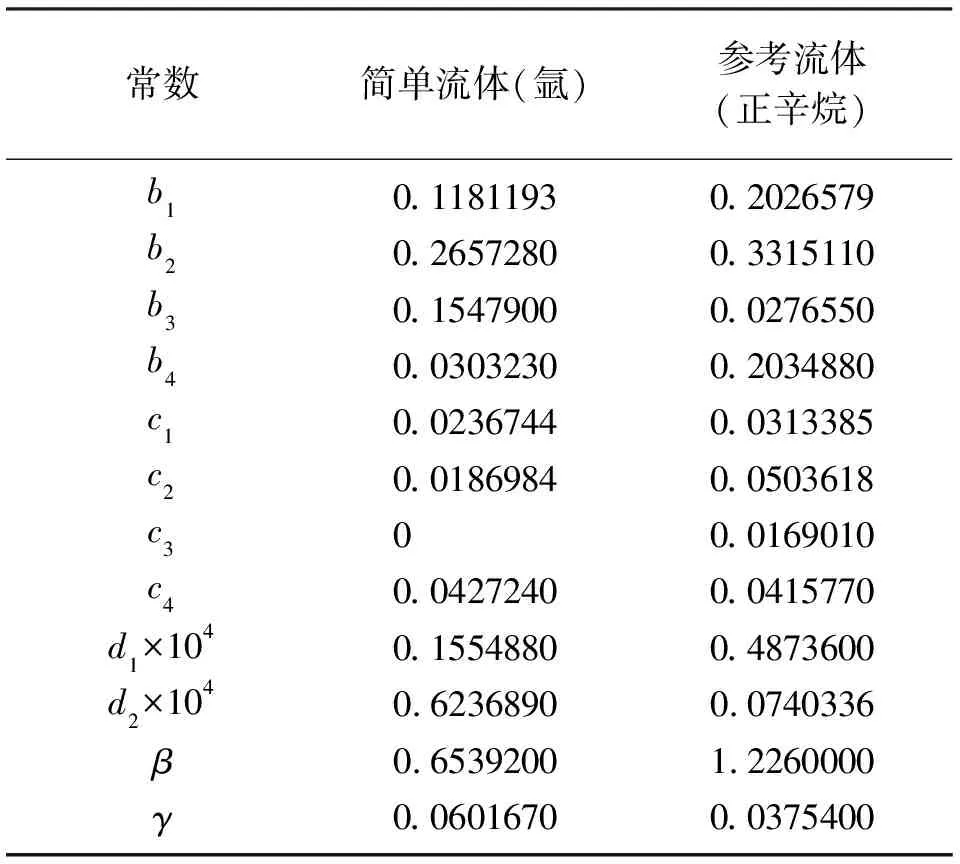
表1 Lee-Kesler方程中的常数

表2 常见实际气体的临界参数和偏心因子数据

为实现压缩因子的计算，采用PLC编程语言编写计算Zi的功能块V_cal，如图2所示。其输入变量是pr和tr，输出变量中，zr即公式中的Z(0)，rzr即公式中的Z(r)。程序调用减法SUB和除法DIV函数，输出变量z1即公式中的Z(1)。图中的0.6336是偏心因子，Z是最终计算的压缩因子。

某乙醇蒸汽的温度和压力：p=689.01kPa，T=427.2K。根据表2，pc=6384 kPa，Tc=516.25K，运算结果：Z(0)=9.3356729E-001；Z(1)=-4.2348217E-002。因此，压缩因子是0.90673548，图2显示计算程序运行结果。实际查表结果计算的压缩因子是0.90673548，表明采用PLC实现压缩因子的计算具有很高计算精度。

某电厂过热蒸汽设计压力3.0MPa(A)，温度400℃，设计密度为10.2426kg/m3。现工况压力为3.1MPa(A)，温度410℃，如果仅用温度压力补偿，计算得密度为10.4291kg/m3。而实际密度为10.5877kg/m3，可见仅用温度、压力补偿的密度值较小，误差达-1.5%。如果加入压缩因子补偿，则实际密度为10.5797kg/m3，误差缩小，为0.0756%，由此可见压缩因子补偿的重要性。

计算实际气体压缩因子的另一种方法是直接查表，由于Lee-Kerler方程不仅提供上述计算方法，而且也提供了对比温度在0.3～4.0，对比压力在0.01～10.00时的压缩因子数据，因此，查表在离线计算时是合适的选择。但由于查表时这些数据是实数数据，因此，计算机实施时，数据占用的内存较大，加上采用双线性内插计算公式计算，有一定误差。因此，经比较，笔者认为采用上述第一种计算方法可在PLC直接实施，是解决实际气体流量密度补偿的有效手段。

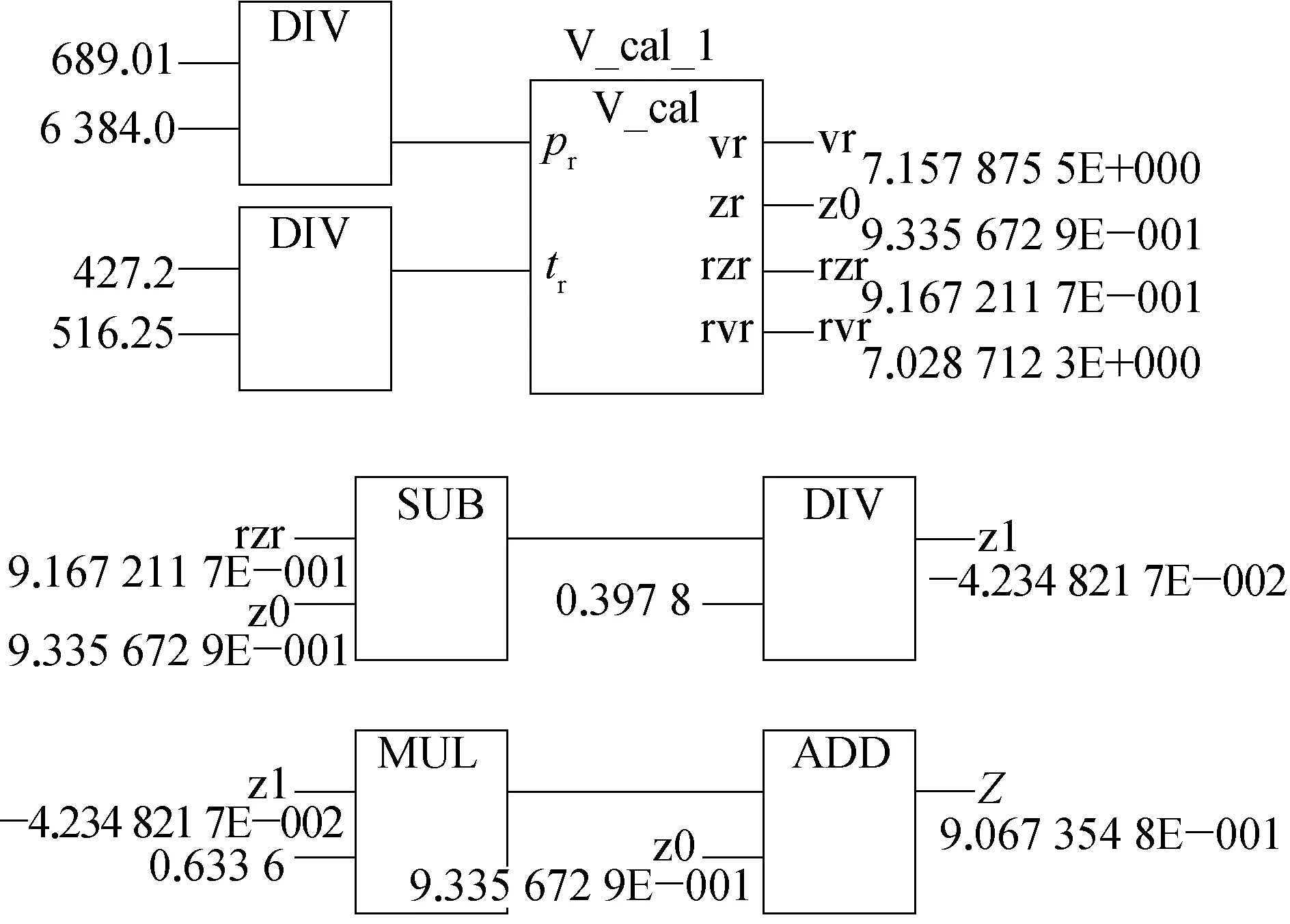
图2 计算压缩因子的PLC程序计算结果

3 实际气体的流量补偿

标准工况和实际工况的压力和温度不一致，因此，可采用下列公式计算实际工况下的理想气体密度。

(5)

式中：下标n——标准状态下的参数；没有下标——工作状态下的参数；ρ——气体密度，kg/m3；p——气体压力，Pa；T——气体温度，K。

考虑实际气体与理想气体的偏差，实际气体的密度补偿公式如下式所示：

(6)

采用PLC和上述Lee-Kesler方程计算压缩因子，则实际气体的流量计算公式可表示为

(7)

式中：C——流量系数；D——管道内径；β——径比；ε——可膨胀系数；Δp——差压。

4 结束语

实际气体的流量补偿不能仅考虑对其温度和压力进行补偿，还需要对压缩因子进行补偿。文中提供了计算实际气体压缩因子的PLC实施方案，是实际气体流量补偿的改进，对提高气体流量测量精度是有效的。

参考文献：

[1]SMITH J M， VAN NESS H C， ABBOTT M M. Introduction to Chemical Engineering Thermodynamics[M]. 7th ed.刘洪来，译.北京：化学工业出版社，2008.

[2]施海云.化工热力学[M].上海：华东理工大学出版社，2007.

[3]郑丹星.流体与过程热力学[M].北京：化学工业出版社，2005.

[4]彭瑜，何衍庆.IEC61131-3编程语言及应用基础[M].北京：机械工业出版社，2009.

[5]何衍庆，何乙平，王朋.常用PLC应用手册[M].北京：国防工业出版社，2008.

[6]缪玲梅，李珍华.用PLC的反馈变量作为迭代变量计算压缩因子[J].医药工程设计，2013，34(01)：5-7.

[7]中国石化集团上海工程有限公司.化工工艺设计手册(上)[M].4版.北京：化学工业出版社，2009.

[8]CHOPEY N P. Handbook of Chemical Engineering Calculations[M]. 3rd ed. 朱开宏，译.北京：中国石化出版社，2005.

[9]周人，何衍庆.流量测量和控制实用手册[M].北京：化学工业出版社，2013.

[10]纪纲.流量测量仪表应用技巧[M].北京：化学工业出版社，2009.

[11]李言伟.天然气流量计量中确定压缩因子的方法[J].化工自动化及仪表，2013，40(01)：12-15.