保持多项式子空间的三阶非线性平方算子的分类

屈 改 珠

(渭南师范学院数学与信息科学学院，714000，陕西 渭南)

保持多项式子空间的三阶非线性平方算子的分类

屈 改 珠

(渭南师范学院数学与信息科学学院，714000，陕西 渭南)

利用不变子空间方法研究三阶非线性平方算子，得到了三阶非线性平方算子在它所容许的多项式不变子空间中的分类，从而求出相应方程的精确解。文中的结果推广了不变子空间理论在非线性偏微分方程中的应用。

不变子空间；三阶非线性平方算子；广义分离变量解

0 引言

不变子空间方法最初由Galaktionov提出，它是与广义条件对称[1-4]密切相关的构造非线性偏微分方程精确解的非常有效的方法。在文献[5]中，Galaktionov利用不变子空间方法研究带有二次非线性项的演化方程的广义分离变量解。事实证明，很多来自于数学、工程学、物理学等领域的非线性演化方程(组)的精确解都可以由不变子空间方法得到[6-9]。

下面介绍不变子空间方法。考虑一阶演化方程

ut=F[u]

(1)

同时Ci(t)满足下面的有限维动力系统：

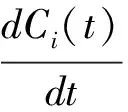
注意到Wn=L{f1(x),…,fn(x)}是由n阶线性常微分方程的解空间生成

L[y]≡y(n)+an-1(x)y(n-1)+…+a1(x)y′+a0(x)y=0

(2)

从式(2)可以得到Wn关于F的不变条件为

L[F[u]]|[H]≡0

(3)

这里用[H]表示方程L[u]=0以及它关于x求各阶导数后的等式。

1 主要结果

本文主要利用不变子空间方法研究允许多项式不变子空间的三阶非线性平方算子

F[u]=b1(uxxx)2+b2uxxuxxx+b3uxuxxx+b4uuxxx+b5(uxx)2+b6uxuxx+b7uuxx+b8(ux)2+b9uux+b10u2

(4)

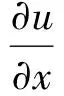
根据最大维定理，讨论微分算子(4)容许多项式不变子空间Wn，n=2,…,7，即

Wn=L{1,x,…,xn-1},n≥2

(5)

命题1：多项式不变子空间(5)在三阶非线性平方算子(4)下不变，仅存在以下情况：

1)当n=2时，有b10=0，即

F[u]=b1(uxxx)2+b2uxxuxxx+b3uxuxxx+b4uuxxx+b5(uxx)2+b6uxuxx+b7uuxx+b8(ux)2+b9uux；

2)当n=3时，有b9=b10=0，即

F[u]=b1(uxxx)2+b2uxxuxxx+b3uxuxxx+b4uuxxx+b5(uxx)2+b6uxuxx+b7uuxx+b8(ux)2；

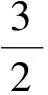
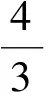
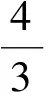
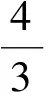
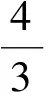
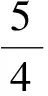
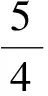
证明过程类似于文献[7]。下面给出2个求相应偏微分方程精确解的例子。

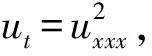
u(x,t)=c1(t)+c2(t)x+c3(t)x2+c4(t)x3+c5(t)x4+c6(t)x5+c7(t)x6，

其中ci(t)满足下面的常微分方程组

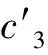
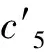
求解上述方程组，可得原方程具有以下形式的解

u=(b-6x)(b5-30b4x-72b3x2-4 752b2x3-7 072bx4-7 776x5)/46 656(T-14 400t)，

这里b是任意正实数，T>0是爆破时间，该解在T=14 400t时刻爆破。

u(x,t)=c1(t)+c2(t)x+c3(t)x2+c4(t)x3，

同时ci(t)满足有限维动力系统

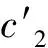
求解上述方程组，可得原方程具有以下形式的解

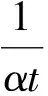
该解当t→0时发生爆破。

[1] Fokas A S,Liu Q M.Generalized conditional symmetries and exact solutions of nonintegrable equations[J].Theor Math Phys,1994,99:263-277.

[2]Fokas A S,Liu Q M.Nonlinear interaction of traveling waves of nonintegrable equations[J].Phys Rev Lett,1994,72:3293-3296.

[3]Zhdanov R Z.Conditional Lie-Backlund symmetry and reduction of evolution equations[J].J Phys A:Math Gen,1995,28:3841-3850.

[4]Qu C Z.Group classification and generalized conditional symmetry reduction of the nonlinear diffusion co-

nvection equation with a nonlinear source[J].Stud Appl Math,1997,99:107-136.

[5]Galaktionov V A.Invariant subspaces and new explicit solutions to evolution equations with quadratic nonlinearities[J].Proc Royal Soc Edinburgh,1995,125:225-246.

[6]Svirshchevskii S R.Symmetries of linear ODEs and generalized separation of variables in nonlinear equations[J].Phys Lett A,1995,199:344-348.

[7]Galaktionov V A,Svirshchevskii S R.Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics[M].London:Chapman and Hall/CRC,2007.

[8]Qu C Z,Zhu C R.Classification of coupled systems with two-component nonlinear diffusion equations by the invariant subspace method[J].J Phys A:Math Theor,2009,42:475201-475227.

[9]Ma W X.A refined invariant subspace method and applications to evolution equations[J].Sci China Math,2012,55:1769-1778.

ClassificationofThird-orderNonlinearQuadraticOperatorsPreservingPolynomialSubspaces

QU Gaizhu

(School of Mathematics and Information Science,Weinan Normal University,714000,Weinan,Shannxi,PRC)

Using the invariant subspace method,the third-order nonlinear quadratic operators is discussed,the full classifications of polynomial invariant subspace admitted by the third-order quadratic operators are derived,moreover,some explicit solutions to the resulting evolution equations with third-order nonlinear quadratic operators are constructed.The obtaining results further extend the applications of invariant subspace theory in the PDEs.

invariant subspace;third-order nonlinear quadratic operators;generalized separation of variables solution

2014-08-28;

2014-10-08

屈改珠(1978-)，女，陕西蒲城人，讲师，博士研究生，从事偏微分方程研究。

国家自然科学基金项目(11371293)；陕西省教育厅基金项目(14JK1246)；陕西省军民融合研究基金项目(13JMR13)；陕西省重点学科数学学科基金项目(14SXZD015)；渭南市基础研究计划项目(2013JCYJ-4)。

10.13990/j.issn1001-3679.2014.05.001

O175.29

A

1001-3679(2014)05-0571-03