粒子在势场中微分散射截面的理论计算

穆爱霞

(平凉医学高等专科学校，甘肃 平凉 744000)

电子与原子分子的散射过程在天气物理、等离子体物理以及生物体系的辐射损伤中都是非常重要的，微分散射截面理论计算的研究成果则可为以上各领域实验现象的解释、可观测量的预言提供大量的参考信息[1]。目前，大多数研究注重微分散射截面的数值图表展示，虽然结果展示相对直观清晰，但具体的理论推导过程暂不清晰[2-4]。针对这一问题, 我们根据经典量子力学和Born-Oppenheimer的方法，通过理论公式推导，计算出粒子在不同势能函数下的微分散射截面和相移，为其在数值研究上做好铺垫，更为散射过程的数值模型提供有效检测方法，旨在使数值与理论方法得以相互补充，使该研究领域内容更加丰富全面。

1 电子在势场V(r)=V0/r2(V0>0)中的微分散射截面

(1)

令

Ψ(r,θ)=∑r-1fl(r)Pl(cosθ)

(2)

(3)

其中U(r)=2mV(r)/ħ2,k2=2mE/ħ2。

将V(r)=V0/r2代入(3)式，并令

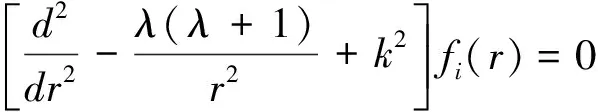
(4)

(4)式满足边界条件。

当r→0,∞时，fl(r)有界的解为

fl(r)=krjl(kr)=Sl(kr)

(5)

(5)式的渐进解形式为

(6)

(7)

经比较，可得l分波的相移

(8)

散射振幅为

(9)

微分散射截面为

(10)

对于s分波(l=0)

(11)

2 电子在势场V(r)=Ae-a2r2中的微分散射截面

按Born一级近似，散射振幅为

(12)

所以，微分散射截面为

(13)

总截面为

(14)

3 结论

以上理论推导方法为粒子在不同势场中的散射研究提供了一个足够准确的微分散射截面计算公式, 如选择合理的、准确的参数，可利用本文的研究结果来验证其他文献中的数值解。同时也可以运用此类方法，理论推导出粒子在其他势场中的微分散射截面所满足的方程，更好地解释或预言散射计算中的可观测数据，使理论研究与数值研究达到完美结合。

参考文献：

[1]杨向东.原子和分子碰撞理论计算及程序[M].成都:电子科技大学出版社,1992.124-140.

[2]汪荣凯,余春日,令狐荣锋,杨向东.He-N2碰撞体系相互作用势及微分散射截面的研究[J].四川大学学报(自然科学版),2006,43(2):371-375.

[3]蒋德琼,李旭,魏强.氖原子与H2(D2、T2)分子碰撞微分截面的理论研究[J].四川师范大学学报(自然科学版),2003,26(5):486-489.

[4]蔡凤鑫，栗增，罗有华.低能电子与氮原子弹性散射截面的理论计算[J].河南大学学报(自然科学版),1997,22(4):1-5.