委托代理关系下代理人参与契约保留效用的贝叶斯估计

张 瑞， 唐海军

(四川文理学院 数学与财经学院，四川 达州 635002)

1 引言

委托代理是指一个人或一些人(委托人)委托其他人(代理人)根据委托人利益从事某些活动，并相应授予代理人某些决策权的契约关系(詹森和麦克林，1976)[1]。在委托代理关系中，存在着所有权和经营权的分离、投资风险、信息不完全和非对称性等问题。委托人想使代理人以自身的利益为目的采取行动，追求自身利益的最大化。但代理人采取的何种行动委托人并不能直接观察得到，所观测的只是一些相关的变量。因代理人的行动影响和外生随机因素的不确定性，所以委托人得到的仅是代理人行动的不完全信息。

基于此种情况，委托人在设计契约时要引入一套激励机制，依据所取得的相关信息对代理人进行奖惩，激励代理人选择对委托人最有利的行动，以期使自身利益最大化。但委托人在进行机制设计时，一般会面临两个约束： “参与约束”与“激励相容约束”[2]。要使代理人参与契约，在激励机制下代理人获得的期望效用要大于或等于他在其它机会下得到的最大期望效用。该最大期望效用定义为代理人的“保留效用”。保留效用反映了代理人参与契约的机会成本。“激励相容约束”中，在代理人的类型不确定的状况下，要促使代理人选择委托人期望的行动，只有代理人在选择该行动时获得的期望效用大于选择其它行动时获得的期望效用，代理人才会采取委托人希望的行动。

在激励机制设计中，满足参与约束的称为“可行机制”。 只有委托人选择适当“可行机制”，代理人才会参与契约，才可能在随后的激励相容约束的机制下采取委托人希望的行动。显然，可行机制的设计十分重要，其中的保留效用对吸引代理人参与契约非常关键。

2 保留效用的贝叶斯估计量

在传统的委托代理框架中，保留效用定义为代理人在其它机会下所获得的最大效用[3]。但实际上，代理人的保留效用不仅因代理人不同而存在差异，而且与代理人的行动和自然状态也存在着联系(其中自然状态为不受委托人和代理人控制的外生变量)。同时一定的行动和自然状态共同决定了可供观察的结果和产出。委托人基于观察结果和产出给出的报酬如何诱使代理人参与契约，在这里对保留效用研究就显得特别重要。

代理人愿意参与契约的保留效用记为U，其分布函数为F(u)。经济行为中，企业根据市场的变化调整产出，而市场受政策、经济形势、竞争者行为、气候等诸多因素的影响，具有一定的随机性。基于一定的行动和自然状态共同决定可供经济活动的结果和产出分别记为X,π，则X与π是随机变量。在委托人基于经济活动的投入和产出结果给出相应的报酬ξ，建立ξ=Φ(X,π)，从而报酬ξ也是一个随机变量，相对应的分布函数为F(ξ;u)。在委托人取得观察结果和产出的样本后，即可确定相应的报酬ξ样本。如取得ξ的样本为ξ1,…，ξn，利用这些样本建立委托人针对代理人的决策函数[4]d(ξ1,…，ξn)，决策函数构建出决策空间记为G。用d(ξ1,…，ξn)去估计代理人愿意参与契约所获得的保留效用u与拒绝参与所得的其他效用之间的损失，损失函数[5]为L[u,d(ξ1,…，ξn)]。在代理人参与契约的条件下，所获的保留效用至少不会小于他从事其他事务所获的效用，这两者之间的损失总是非负的，对应的损失函数需满足

L[u,d(ξ1,…，ξn)]≥0

决策函数的贝叶斯风险函数

B(d)=E{E(L[u,d(ξ1，…，ξn)]|ξ1，…，ξn)}

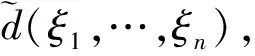
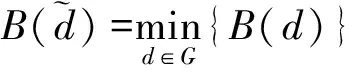
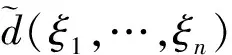
3 基于平方差损失函数的贝叶斯估计

3.1 平方差损失函数

损失函数是判断决策的优劣程度量。即当参数取值为θ时，选择决策d所形成的损失L(θ,d)越小，说明选择的决策越趋向于正确。平方差损失是指L(θ,d)=(θ-d)2。委托代理中，在设计可行机制时确定保留函数的过程中，选择决策函数d(ξ1,…，ξn)时，对应的平方差损失函数为

L[u,d(ξ1,…，ξn)]=[u-d(ξ1,…ξn)]2

由文献[6]，若损失函数为平方差损失函数，且

则u的贝叶斯估计量为

E[u-d(ξ1,…ξn)]2<∞

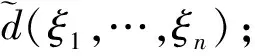
当U为连续型且有密度函数π(u)时，

当U为离散型且有取值为uj时

其中h(u|x1,…,xn)为在(ξ1,…，ξn)=(x1,…，xn)条件下U的条件密度函数。在损失函数为平方差损失函数时，保留效用就可用E[u|ξ1,…,ξn]来替代。

3.2 正态分布假定下保留效用的贝叶斯估计

李心愉[7]的研究表明，在经济环境较为稳定，企业稳步发展过程中，企业的投入产出服从正态分布。企业的委托代理关系中，委托人基于投入和产出结果给出相应的报酬ξ也成正态分布。取ξ～N(u,1)，ξ1,…，ξn为ξ的样本。同时代理人愿意参与契约的保留效用U具有一定的随机性，服从正态分布，为U～N(0,1)。

对应平方差损失函数为

L[u,d(ξ1,…，ξn)]=[u-d(ξ1,…，ξn)]2，

在报酬ξ取样本为ξ1,…，ξn时，ξ=(ξ1,…，ξn)′，X=(x1,…，xn)′，

h(u|X)∝π(u)f(X|y)

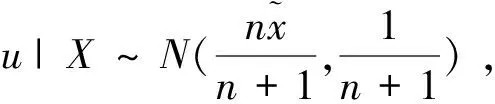
其中π(u)为U的密度函数，f(X|u)为在U=u下，(ξ1,…，ξn)的条件密度函数。

∝含义为如果函数f(x)与函数φ(x)只相差一个常数因子，则称φ(x)为f(x)的核，记为f(x)∝φ(x)

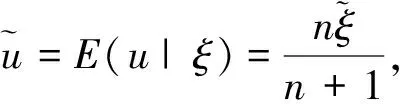
4 结束语

传统的委托代理中，没有给出确定保留效用的具体可行的方法。此研究结合了实际投入和产出结果给出了贝叶斯风险函数，得到保留函数的贝叶斯估计量，从而找到了一种求保留效用的方法。这也使得在参与约束中保留效用的含义更一步清楚和明确。但在此研究中，委托人如何根据观察结果和产出确定相应的报酬；对不同的损失函数，所对应的贝叶斯估计量又有何区别等。这些都是值得进一步探讨的问题。

参考文献：

[1]向荣,贾生华.对代理理论的综述与反思[J].商业经济与管理,2001.

[2]朱恒鹏.委托-代理理论[M].现代经济词典,2005.

[3]苏玉珠.代理理论的形成及基本观点[J].陕西经贸学院学报，2000,13(1)：76-79.

[4]唐小我,曾勇,李仕明等.管理经济分析理论与应用[M].成都：电子科技大学出版社，2000.

[5]孙荣恒,应用数理统计[M].北京：科学出版社,2003.

[6]梁之辉,邓集贤等.概率论与数理统计[M].北京：高等教育出版社,2005.

[7]李心愉.投入产出分析方法再认识-在正态分布假定下考察投入产出关系[J].经济研究,1992.