编织-嵌槽型金属橡胶的压缩性能研究

李 拓, 白鸿柏, 路纯红, 曹凤利

(军械工程学院,石家庄 050003)

图1 编织-嵌槽型金属橡胶

编织-嵌槽型金属橡胶是采用编织-嵌槽工艺制成的新型弹性阻尼材料，具有类似弹簧的螺旋结构，可以像橡胶一样应用于隔振器以实现对相关系统的减振作用[1-2]，如图1所示。编织-嵌槽型金属橡胶的制备过程为：首先使用专用编织设备(如圆纬针织机)将选取的金属丝编织成网套，再根据需要剪裁、称取一定质量的网套，并将截取的网套经预压整形、冷弯成型等工艺轧制出若干道沟槽，然后将网套缠绕成毛坯，使沟槽嵌合在一起，最后对毛坯进行冷冲压成型。和由金属丝经螺旋卷缠绕、定螺距拉伸、铺设毛坯、冷冲压等一系列工序制成的金属橡胶[3]相比，编织-嵌槽型金属橡胶很好地克服了低刚度金属橡胶构件成型质量较差、使用过程中材料残余变形大，尺寸及性能稳定性较差等不足。

国内外均有对针织材料压缩性能研究的报道。国外一些学者[4-7]发现1×1棱纹和米兰绒纬编针织复合材料的压缩强度显著高于其拉伸强度。改变针织圈长度和针脚密度对材料压缩性能的影响并不明显。Khondker等[4]研究了E玻璃/乙烯脂纬编针织复合材料(平针、棱纹和米兰绒结构)，发现随针织圈长度的增加，压缩模量变化不大。一些国内的学者也进行了相关研究。梁子青等[8]对预定型织物在压实阶段的可压缩性以及压缩过程中纤维体积含量的变化特点进行了研究，发现预定型织物压实后的纤维体积分数趋于一致，并与压缩织物的层数关系不明显。马悦等[9]通过试验研究发现轴向数、纤维束间夹角以及湿润作用均会对织物的压缩性能产生影响。

编织-嵌槽型金属橡胶同以上各种针织材料的主要不同点在于其是由金属丝制成的，其压缩特性同以上各种针织材料可能会有一定的差别。因此针对这一新型阻尼材料开展压缩性能方面的研究，对探寻其结构参数与宏观力学性能之间的联系是十分有必要的，这将对编织-嵌槽型金属橡胶的优化设计以及进一步的研究具有重要的指导意义。

1 编织-嵌槽型金属橡胶静态压缩试验

1.1 试验设备及试验元件

试验设备选用济南天辰WDW-T200型电子万能试验机。该试验机适用于金属、非金属材料的拉伸、压缩及弯曲等力学特性试验，位移分辨率为0.001 mm，最大试验力为200 kN。试验件选用304不锈钢丝制备。三个试验件的密度和成型面直径均相同，为0.54 g/cm3、32 mm。三个试验件其他的工艺参数如表1所示。

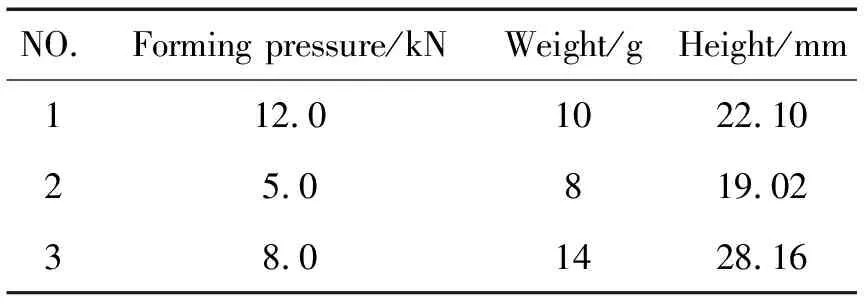
表1 试件工艺参数表

1.2 试验及结果分析

试验的加载方式选用位移控制，加载速度为1.5 mm/s，最大压缩位移确定为11.50 mm。

根据采集的数据绘制试验件的载荷-位移曲线，如图2所示。

图2 三个试验件的载荷-位移曲线

图2中，三个试验件的载荷-位移曲线变化趋势基本相同，故取其中1号试验件的载荷-位移曲线进行研究，如图3所示。

图3 1号试件的载荷-位移曲线

由图3可知，载荷-位移曲线大致可以分为两个阶段。

第一阶段(OA段)载荷和位移的关系接近线性，故称之为线性阶段。

在将编织-嵌槽型金属橡胶构件从模具中取出后，由于失去约束，构件会发生膨胀，产生弹性反冲，使部分因压缩而产生接触的金属丝发生分离，金属丝之间产生空隙。

和金属橡胶构件类似，编织-嵌槽型金属橡胶构件在承受压缩载荷时，其内部金属丝的接触往往开始于构件的最小密度区，且随着压缩载荷的增大扩展至大密度区[3]。因此，在压缩变形初期，随着压缩载荷逐渐增大，螺旋结构之间的间隙不断减小。而金属丝之间的空隙相对较小，故在压缩初期变化不大。成型方向上金属丝网层数较多，每一层金属丝网的压缩变形量很小，线圈的结构形态几乎不变，故构件的刚度近似为一定值。

第二阶段(AB段)随着压缩位移的增大，刚度逐渐增加，故称之为硬化阶段。

刚度的升高是由金属丝随着接触载荷的不断增大而产生的弯曲扭转变形引起的。另外，金属丝之间接触点数目的增加，使接触点之间的跨度减小，这也在一定程度上使构件的刚度增大。

2 细观结构分析

2.1 编织-嵌槽型金属橡胶的细观结构

根据编织-嵌槽型金属橡胶的工艺特点，金属丝网之间呈叠层嵌合结构关系，如图4所示。

图4 金属丝网间的叠层嵌合结构

线圈是金属丝网的基本单元，由针编弧和圈柱两部分组成[10]，如图5(a)所示。线圈的几何形态呈三维弯曲空间曲线。在金属丝网上，线圈在横列方向是连接在一起的，而在纵列方向则形成串套勾连结构，如图5(b)所示。

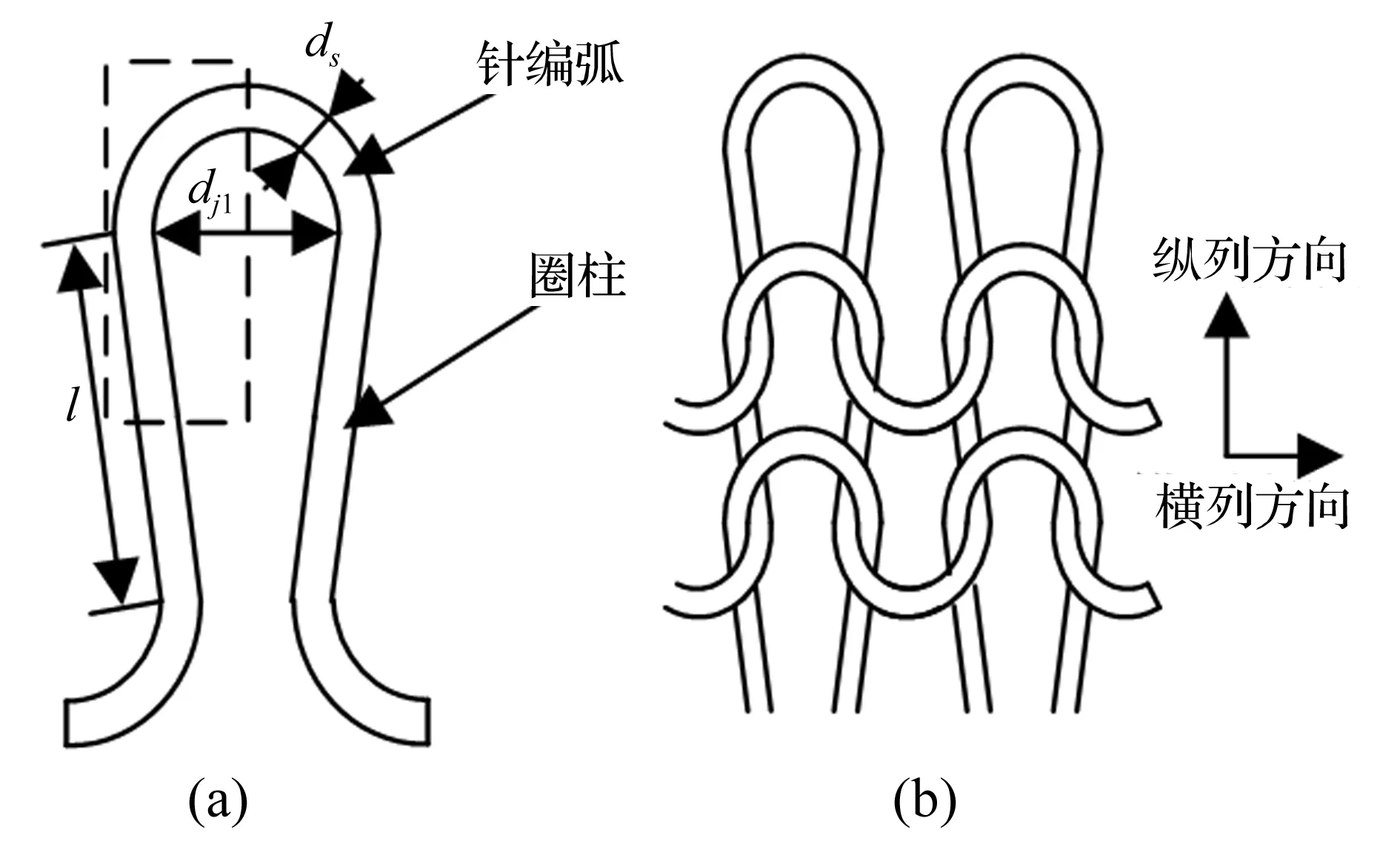
图5 线圈的基本结构(a)和连接形式(b)

2.2 结构单元的提取

编织-嵌槽型金属橡胶内部线圈的形态及分布情况比较复杂，为便于提取结构单元，特提出以下三点假设：

(1) 相对于整个构件来说，线圈足够小。因此，位于叠层部分相互串套的线圈可近似认为其针编弧对称面相同、圈柱共面。

(2) 经过冷弯轧制沟槽、冷冲压成型等工序后，位于嵌合部分的线圈发生了弯曲扭转变形。变形发生在针编弧部分，变形前后线圈的长度不变。

(3) 在构件承受压缩载荷时，线圈间接触点处的接触载荷大小相等。

为研究材料内部金属丝之间的空间结构关系，沿虚线框截取部分金属丝网，如图6(a)所示，截面ABF、ECD均为针编弧的对称面，AE、FD过圈柱中点，G、H、I、J为金属丝之间的接触点，θ2为针编弧所在平面同圈柱所在平面的夹角。

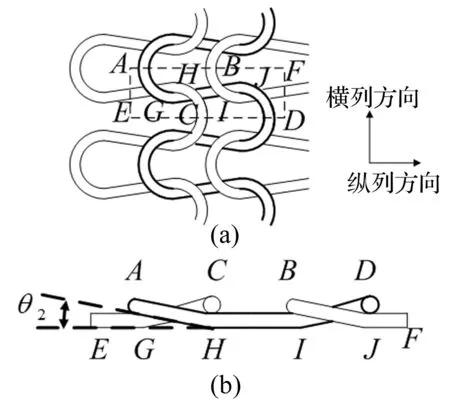
图6 金属丝网结构(a)和金属丝网截面图(b)

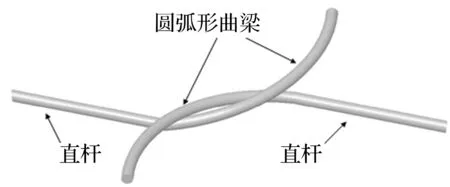
图7 结构单元

图6中AD段金属丝由两个四分之一圆周长的针编弧和一段完整的圈柱组成，其长度等于线圈的一半。虚线框内的金属丝网包括两组完全相同的串套勾连结构，提取其中一组作为一个结构单元，如图7所示。每段线圈均可简化为由圆弧形曲梁和直杆连接而成的结构，如图5(a)虚线框部分所示。

由于构件是经卷缠制成的，金属丝网上存在一定的拉力使线圈拉紧，因此可认为结构单元接触点的位置即为曲梁和直杆的分界处。观察图6(b)，在构件承受压缩载荷时，直杆两端会受到大小方向均相同的压力作用，因此在直杆上没有出现新的接触点之前，直杆不会发生变形。弹性范围内，编织-嵌槽型金属橡胶的变形源于结构单元内曲梁的变形。

经过轧制沟槽和冷冲压成型等工序后，弯折处金属丝网的变形导致结构单元内曲梁的形态发生变化，因此对于编织-嵌槽型金属橡胶构件而言，其内部的结构单元可以分为两类：一类位于金属丝网的嵌合部分，另一类位于金属丝网的叠层部分。

2.2.1 嵌合部分结构单元

在构件冲压成型后，嵌合部分结构单元内的曲梁在弯曲扭转作用下产生了变形。变形后的勾连结构同金属橡胶内螺旋卷的勾连结构类似，故嵌合部分结构单元内的曲梁可看作四分之一圆周长的螺旋形悬臂曲梁[11]，如图8所示。

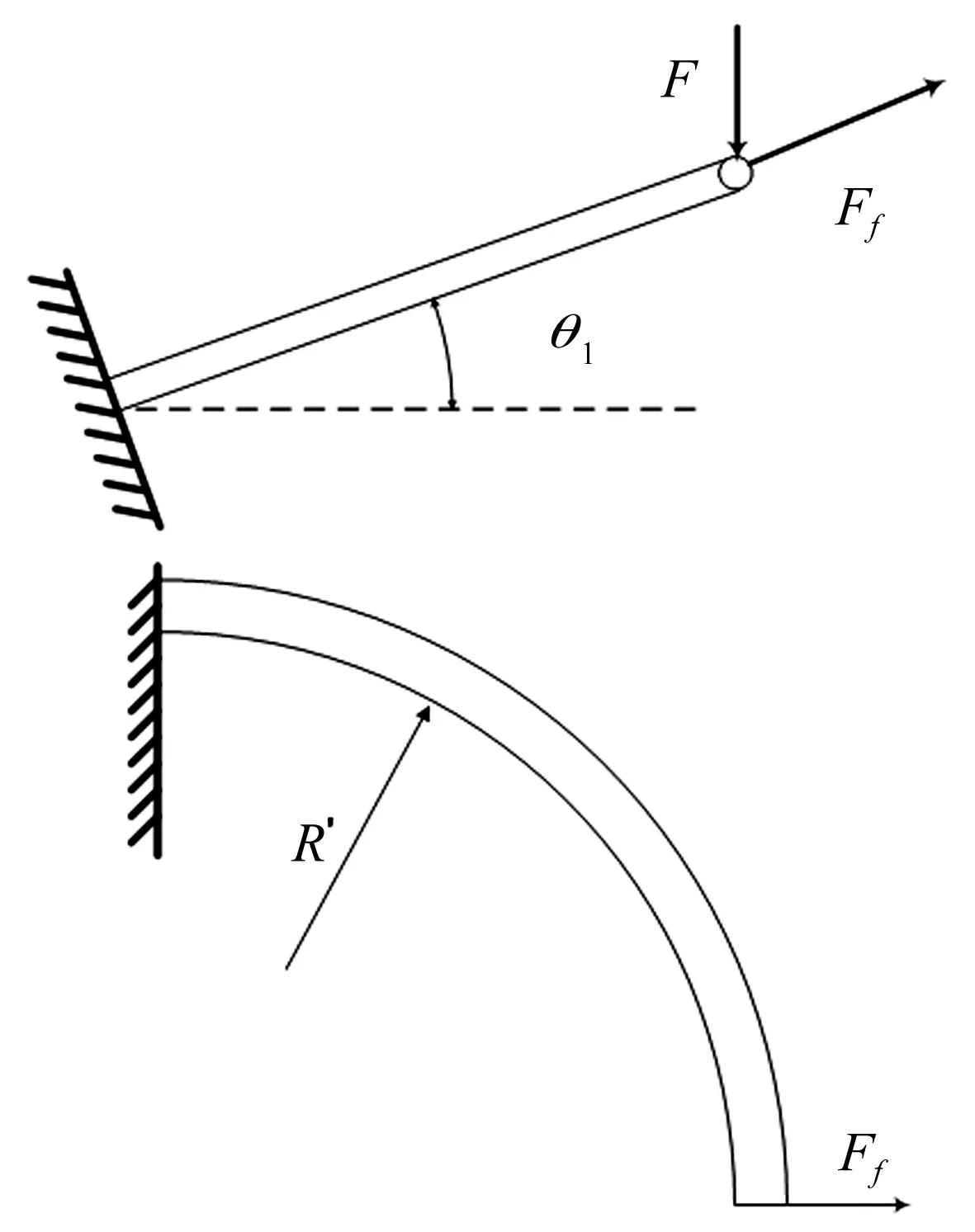
图8 嵌合部分螺旋形悬臂曲梁

螺旋形悬臂曲梁在自由端主要受到两个力，分别为由压缩载荷引起的压力F以及金属丝间发生相对滑动而产生的摩擦力Ff1，与该二力正交方向上可能存在的力或约束对压缩载荷方向上的变形不产生影响，因此不予考虑。由文献[12]可知，在压力和摩擦力的共同作用下，螺旋形悬臂曲梁的刚度Ke1为：

(1)

式中:ds为金属丝的直径，dj1为螺旋形悬臂曲梁的直径，θ1为螺旋形悬臂曲梁的螺旋角，μ为金属丝之间的摩擦系数，G为金属丝材料的剪切模量，E为金属丝材料的弹性模量。

嵌合部分结构单元包含有两段螺旋形悬臂曲梁，结构单元刚度Ku1可以认为是两个悬臂曲梁刚度的叠加：

(2)

2.2.2 叠层部分结构单元

在构件承受压缩载荷时，叠层部分结构单元内部的两段曲梁相互之间有力的作用。对于其中任意一段曲梁，其受到的压力有两个，一个作用在直杆和曲梁的分界处，一个作用在曲梁上。其中，分界处的压力对悬臂曲梁的变形不产生影响。

根据提取结构单元时对结构单元的受力分析可知，结构单元的压缩变形即为曲梁在压缩方向的变形。在构件的压缩过程中，曲梁在接触点处受到两个力，分别是相接触的曲梁提供的压力和相对滑动而产生的摩擦力。正交方向的力对压缩方向的变形不产生影响，因此不予考虑。该部分曲梁的受力情况如图9所示。

图9 叠层部分曲梁

叠层部分结构单元在压缩方向上的刚度Ku2可用两段曲梁刚度的叠加表示。根据卡式定理，可计算得到：

(3)

其中：

B=4α-4sinα-4sinαcos2θ2+

3sin2αcos2θ2-2αcos2αcos2θ2

D=(4sinα-3sin2α+2αcos2α)sin2θ2

式中：dj2为曲梁的直径，α为接触点与圆心连线OA同分界点与圆心连线OH的夹角，θ2为针编弧所在平面同圈柱所在平面的夹角。

由图9可知，有如下几何关系成立：

故角α和θ2的关系可表示为：

(4)

3 编织-嵌槽型金属橡胶的本构关系模型

3.1 本构关系模型的建立

观察图4和图6可知，金属丝网上每一纵列的结构单元串联在一起组成了一个弹性系统，而每一个这样的弹性系统之间是并联的关系，如图10所示。

图10 结构单元组成的弹性系统

因此，以每一个纵列上的所有结构单元为一整体，其刚度Kcourse可以表示为：

(5)

式中:Ncu1、Ncu2分别为每一个纵列上嵌合部分单元和叠层部分单元的数目。

故构件的刚度Kl可以表示为：

(6)

式中:Nwale为构件内部金属丝网横列的数目。

易知，结构单元的总数目N、横列数目Nwale、纵列数目Ncourse以及Ncu1和Ncu2之间有如下的数量关系：

N=NcourseNwale

另外，纵列的数目等于每一个横列上线圈的数目，该值由针织设备的针数来决定；纵列上嵌合部分单元的数目等于外部螺旋结构的圈数。

根据假设2可知，两类结构单元中包含的金属丝长度相等。所以，编织-嵌槽型金属橡胶内部结构单元的总数目N可以通过构件的总质量除以结构单元的质量得到(不考虑制备过程中线圈的破坏)，即：

(7)

式中:m为编织-嵌槽型金属橡胶构件的质量，mu为结构单元的质量。

每个结构单元的质量等于线圈质量的一半。因此，结构单元的质量可表示为：

式中:ρs为金属丝的密度，l为圈柱的长度。

结构单元的总数目可进一步表示为：

(8)

构件整体的刚度关系式(7)可以最终表达为：

(9)

根据经验公式，金属橡胶的恢复力应表示为：

(10)

一般情况下，本构关系式多取到位移的三次方项，故编织-嵌槽型金属橡胶构件的本构关系可以初步表示为：

F=Kl(ξ1x+ξ2x3)

(11)

式中:ξ1、ξ2为修正系数。

由压缩试验数据可知，编织-嵌槽型金属橡胶所承受的载荷-位移关系随着位移的增大呈非线性特性，如图3所示：随着位移的变化，载荷-位移关系接近线性；之后在位移增大到一定程度后，该关系变为硬特性。

根据式(11)进行分析，压缩试验的第一阶段为线性阶段，故ξ2应为一无限小量，但是试验的第二阶段为硬化阶段，这就要求ξ2不能为无限小量。仅包含位移一次方项和三次方项的本构关系式(11)显然不能正确地表达压缩过程中载荷和位移的关系。故将(11)式进一步修正为：

F=Kl(ξ1x+ξ2x3+ξ3x5)

(12)

3.2 计算结果与试验结果的比较

用压缩试验中1～3号试件的试验数据由最小二乘法可获得修正系数ξ1、ξ2、ξ3。根据式(12)对1号试件进行计算，并将得到的计算结果同试验数据进行比较，如图11所示。

图11 计算结果与试验结果比较

由两条曲线的对比可知，建立的本构模型基本上可以描述这种成型方向上的载荷-位移关系。模型可较准确地描述载荷-位移曲线的线性阶段，而对硬化阶段的描述则有一定的偏差。这一问题产生的主要原因是硬化阶段结构单元几何参数的变化。由于编织-嵌槽型金属橡胶多工作在线性阶段，所以，以上本构关系模型可以满足要求。

4 结 论

综合以上分析，不难得出如下结论：

(1) 编织-嵌槽型金属橡胶是一种非线性材料。其压缩变形阶段可分为线性阶段和硬化阶段。

(2) 金属丝之间的摩擦系数、线圈的几何参数等因素都会对编织-嵌槽型金属橡胶构件的刚度产生影响。

(3) 建立了编织-嵌槽型金属橡胶的本构关系模型。通过将理论计算值和试验数据进行比较，发现两者符合程度较好。因此，该本构关系模型能够较好地描述编织-嵌槽型金属橡胶构件在压缩过程中的载荷-位移关系。

[1] 周振凯,徐兵,胡文军等.橡胶隔振器大变形有限元分析[J].振动与冲击,2013,32(5):171-175.

ZHOU Zhen-kai, XU Bing, HU Wen-jun, et al. Large deformation finite element analysis of rubber isolator[J]. Journal of Vibration and Shock,2013,32(5):171-175.

[2] 何小静,上官文斌.橡胶隔振器静态力-位移关系计算方法的研究[J].振动与冲击,2012,31(11):91-97.

HE Xiao-jing, SHANGGUAN Wen-bin. Calculating methods for force versus displacement relation of a rubber islator[J]. Journal of Vibration and Shock,2012,31(11): 91-97.

[3] 切戈达耶夫 D，穆留金 O，高尔德金(李中郢译).金属橡胶构件的设计[M].北京:国防工业出版,2000.

[4] Khondker O A, Leong K H, Herszberg I. Effects of biaxial deformation of the knitted glass preform on the in-plane mechanical properties of the composite[J]. Composites,2001(32):1513-1523.

[5] Leong K H, Falzon P J, Bannister M K, et al. An investigation of the mechanical performance of weft-knit glass/epoxy composites[J].Comp. Sci. & Tech., 1998(58): 239-251.

[6] Leong K H, Nguyen M, Herszberg I. The effect of deforming knitted glass fabrics on the basic composite mechanical properties[J]. J. Mat.Sci., 1999(34):2377-2387.

[7] Wang Y, Gowayed Y, Kong X, et al. Properties and analysis of composites reinforced with e-glass weft-knitted fabrics[J]. J. Comp. Tech.& Res.,1995(17):283-288.

[8] 梁子青,唐邦铭,李艳亮,等.织物预成型体的可压缩性研究[J].材料工程，2006(6):5-8,45.

LIANG Zi-qing, TANG Bang-ming, LI Yan-liang,et al. Study on the compressibility of fabric performs[J]. Journal of Materials Engineering, 2006(6):5-8,45.

[9] 马悦,李炜,梁子青.经编多轴向织物的压缩性能研究[J].材料工程,2007(11):28-32.

MA Yue, LI Wei, LIANG Zi-qing. Compressibility and spring-back behavior of multi-axial warp knitting fabric[J]. Journal of Materials Engineering,2007(11):28-32.

[10] 龙海如.针织学[M].北京:中国纺织出版社,2008.

[11] 马艳红,郭宝亭.金属橡胶材料静态特性的研究[J].航空动力学报,2004,19(3):326-331.

MA Yan-hong, GUO Bao-ting. Static characteristic of metal-rubber[J]. Journal of Aerospace Power, 2004,19(3): 326-331.

[12] 王尤颜,白鸿柏,刘远方.金属橡胶材料压缩性能的细观特征研究[J].机械科学与技术,2011,30(3):404-407.

WANG You-yan, BAI Hong-bai, LIU Yuan-fang. Micro characteristic study of the compressive performance of metal rubber material[J]. Mechanical Science and Technology, 2011, 30(3):404-407.