弯扭耦合影响的MEMS扭转谐振器件中的热弹性阻尼

台永鹏，李 普, 左万里

(东南大学 机械工程学院，南京 211189)

微谐振器是微机电系统(MEMS)的典型器件，广泛应用于高频和高精度的驱动器和传感器。为了获得高性能、高精度，微谐振器件在设计和制造的时候希望能够有非常小的能量损耗和特别高的质量因数。然而，事实证明器件尺度的减小必然导致质量因数的减小。因此，研究微型器件中的能量耗散机理具有重要意义。微谐振器件中有三种主要的能量耗散方式：空气阻尼[1]，支承阻尼和热弹性阻尼。其中，前两种耗散机理可以通过真空封装和合理的结构设计消除。热弹性阻尼是系统所固有的能量耗散机理，不能通过设计制造完全消除。这使得热弹性阻尼经常成为MEMS器件主要的能量耗散机理，决定系统质量因数的上限。近年来，为了设计和制造出高性能的MEMS器件，热弹性阻尼的研究越来越热门。

热弹性阻尼是由热弹性材料中的不可逆热流引起的。当MEMS器件振动时，材料内部必然会产生应变场，其中受挤压的部分温度升高，受拉伸的部分温度降低。产生的温度梯度使不可逆热流从温度高的部分流向温度低的部分。这种由于不可逆热流导致的能量耗散就叫做热弹性阻尼。只要材料的热膨胀系数不为零，热弹性阻尼就必然存在。

在1937年，Zener[2-3]第一次精确计算出了悬臂梁的热弹性阻尼。Zener研究了弯曲振动的悬臂梁，推导出了只考虑厚度b方向热传导的一维热弹性阻尼解析模型：

(1)

式中:E为杨氏模量，α为热膨胀系数，T0为环境温度，Cv为定体积热容，τ为松弛时间。2000年，Lifshitz和Roukes (LR)[4]精炼了Zener的理论，给出了梁在弯曲振动时一维热弹性阻尼的LR模型

(2)

式中:ξ=b×sqrt(ω/(2χ))，其中χ为热扩散系数。Zener模型和LR模型都是计算热弹性阻尼的经典的解析模型，已经得到了实验数据的验证，并广泛应用于MEMS器件热弹性阻尼的预测。这两种理论在建立的过程中都作了如下假设：① 器件的质量因数极高，其谐振频率不受影响；② 应变场与温度场单向耦合，即应变场影响温度场，温度场不影响应变场，因为温度变化非常微小；③ 热传导是一维的，只发生在梁厚度方向，宽度和长度方向因为热传导比较微弱而忽略不计。

MEMS谐振器件一般具有简单的结构，容易得到热弹性阻尼的闭合的解析表达式。这些表达式简单而高效，不仅用来预测热弹性阻尼，还可以为数值计算结果提供非常理想的参考和验证模型。比如，一些学者提出了计算二维、三维热弹性阻尼的方法[5，6]，以及层压复合结构、矩形板、圆盘、圆环、碳纳米管中的热弹性阻尼模型。此外，以有限元(FEM)法为主的偏微分方程数值解法能很好地处理复杂几何形状及边界条件，求解复杂形状器件的热弹性阻尼。但是，数值模型的存在局限性也很明显：① 有限元法不能直接体现器件的几何参数与物理性能之间的关系。数值法的方程阶数高，计算效率低，不利于系统级模拟和优化迭代计算，更适合在校核计算中使用。② 很难在短时间内学会熟练使用ANSYS等商业有限元软件。

通常，MEMS谐振器件运行在纯扭转振动模态或者纯弯曲振动模态。热弹性阻尼主要是由弯曲振动模态引起的。而纯扭转模态不会产生体积的变化，没有热弹性阻尼。但是，一些MEMS扭转谐振器件在振动时并不是纯扭转，而是弯扭耦合振动。弯扭耦合不仅影响到器件的动力学特性，而且其弯曲振动的部分不可避免产生热弹性阻尼，影响到器件的性能。目前，在能量耗散方面，MEMS扭转谐振器件的研究主要集中在空气阻尼，也有少量文献涉及热弹性阻尼。然而，在弯扭耦合的MEMS扭转谐振器件中，并没有文献讨论其热弹性阻尼的解析模型。同时，实验数据说明[7-10]，弯扭耦合的单平板和双平板谐振器的热弹性阻尼很重要，不能忽略。

本文考虑了MEMS谐振器件中的弯扭耦合现象，利用弯扭耦合的静态平衡方程和动力学方程推导出支承梁的动力学特性，以此为基础，在假设微平板为刚体的前提下，根据热传导方程和LR理论推导出热弹性阻尼的解析模型。将本文所提出的解析模型与有限元仿真结果相比较，两者的拟合度很高，误差较小，证实了理论的可行性。解析模型与实验数据的比较揭示了热弹性阻尼在内部耗散中的重要性。通过对解析模型特性的研究，本文分析了谐振器件几何尺寸对热弹性阻尼的影响。

1 弯扭耦合MEMS谐振器件的热弹性阻尼模型

1.1 静电力作用下的弯扭耦合振动模型

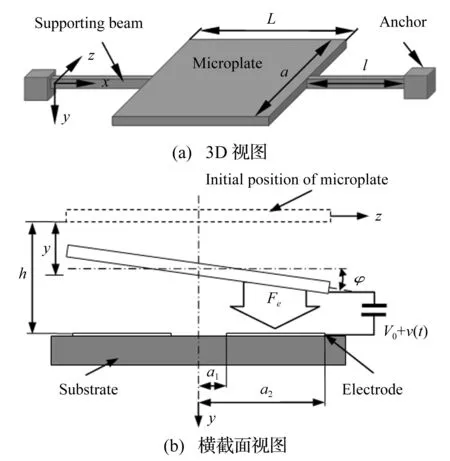
图1 静电驱动的扭转MEMS谐振器件示意图

图1是扭转谐振器件示意图。静电力驱动的微平板由两个支承梁分别固定在锚定上。电极板放置在基底上，位于微平板的下方。微平板的长度和宽度分别为L，a；两根支承梁的长度和宽度分别为l，c；器件整体厚度为b。微平板和电极间施加驱动电压V=V0+v(t)，其中V0是直流偏置分量，v(t)是交流分量，通常V0≫v(t)。假设微平板是刚体，在驱动电压的作用下，产生纵向位移y(t)=y0+δ(t)，以及绕支承梁旋转的角位移φ(t)=φ0+φ(t)，其中y0和φ0是偏置电压导致的偏置位移，δ(t)和φ(t)是交流激励电压导致的动态位移。当施加偏置电压时，该扭转谐振器件的静态平衡方程可表示为[11]

(3)

式中：Ky，Kφ分别表示弯曲刚度和扭转刚度，a1和a2表示电极的位置参数，ε为真空介电常数，h为电极与微平板的间距。矩形截面梁的弯曲刚度和扭转刚度可以表示为

(4)

式中：G为剪切模量；I，Ip分别为梁的截面惯性矩和极惯性矩。

当器件受静电力作用，以频率ω做简谐振动时，微平板的激励电压和动态位移可表示为

v(t)=v0eiωt,φ(t)=φ0eiωt,δ(t)=δ0eiωt

(5)

忽略其他阻尼的影响，系统动力学方程可表示为[12]

(6)

式中：m为微平板质量，Iφ为转动惯量，Fe，Me分别为驱动电压V导致的静电力和静电力矩。将Fe，Me在(V0,φ0,y0)处一阶Taylor展开，然后代入式(6)中，则线性化的动力学方程可以写成

(7)

求解式(7)，得到微平板动态位移之比

(8)

式中：参数AB，BB，CB，AT，BT，CT是Taylor展开得到的常数项；根据式(3)，它们可以进一步用偏置电压V0作用下微平板的偏置位移表示：

(9)

(10)

(11)

(12)

(13)

CT=BB

(14)

式中：g0=h-y0为偏置电压作用下，电极板与微平板的间距。

1.2 简化的微平板动态位移之比

微平板在弯扭耦合振动时会引起它与电极板之间的间距变化。这种变化导致静电力与简谐激励电压间复杂的非线性关系，如式(6)所示。如果微平板在振动时的动态位移非常小，可以忽略微平板与电极板之间间距的变化所导致的非线性静电力。这种情况下，Fe，Me都可看作简谐振动，并且

Me=rFe

(15)

其中：r为平板受力点到扭转轴的距离。将式(15)代入式(6)，得到简化的微平板动态位移之比为

(16)

从上式可以看出，对于简化的模型，微平板动态位移之比只与受力位置和振动频率有关。

1.3 热弹性阻尼计算

考虑弯扭耦合谐振器件做简谐振动。由于微平板看作是刚体，不存在热应变，所以只需要考虑支承梁的热弹性阻尼。支承梁的热传导方程可以表示为[4]

(17)

式中：θ=θ0eiωt为温度变化，ΔE=Eα2T0/Cv为杨氏模量的松弛强度，Y(x,t) =Y0(x)eiωt为梁在y方向的位移。假设用支承梁的挠度曲线近似表示梁的位移。根据边界条件：Y(0) = 0，Y(l) =δ(t)，∂Y(0)/∂x= 0，∂Y(l)/∂x= 0，则Y(x,t)可以表示为[13]

(18)

根据LR理论，温度场方程可以表示为[4]

(19)

通常，材料内部由于温度变化导致的热应力与施加的应力场相比可以忽略不计，所以支承梁x轴方向的应力场和热应变分别表示为

(20)

(21)

整个谐振器件的损失功需要考虑两根支承梁能量耗散的总和为

(22)

一个振动周期里谐振器件最大存储弹性能包含扭转弹性能和振动弹性能两部分为

(23)

根据品质因数Q的定义，利用式(22)和(23)得到热弹性阻尼解析表达式

(24)

式中：pf为弯曲振动存储能量与总存储能量之比。可见，弯扭耦合MEMS扭转谐振器件中的热弹性阻尼为能量比与LR理论结果的乘积。将式(8)和式(18)代入式(24)，可得

(25)

式中：系数D=Kφ/Ky=GIpl2/Eb3c，其数值与材料属性和几何尺寸相关。

2 解析模型与FEM仿真和实验数据比较

2.1 FEM仿真结果比较

为了验证本文解析模型，将解析模型计算结果与有限元(FEM)仿真结果比较。本文采用ANSYS仿真软件进行有限元仿真，其中支承梁利用SOLID226单元建模，这种单元可以仿真三维热弹性阻尼，而微平板利用SOLID45单元建模。假设器件为多晶硅制造，其材料特性参数：E=157 GPa，α=2.6×10-6K-1，泊松比υ= 0.22，密度ρ= 2 330×10-18kg·μm-3，定压热容Cp= 699×1012pJ (kg·K)-1，χ=0.55×10-4m2s-1，ε=8.854×10-6pF μm-1，T0=300 K。表1(模型1)给出了器件基本结构参数，电极板施加电压为V0=20 V，v0=2 V。

表1 MEMS扭转谐振器件的基本结构参数(单位：μm)

图2给出了本文解析模型和FEM数值仿真的比较。如图所示，解析模型曲线与FEM数值仿真曲线拟合度比较好。由于有限元仿真计算的是三维热弹性阻尼，所以它的数值通常比一维计算结果要大，而且计算精度更高。从图中可以看出，在特征频率F0附近，两者相对误差小于10 %；在低频段，两者相对误差甚至小于5 %；在高频段两者误差较大。

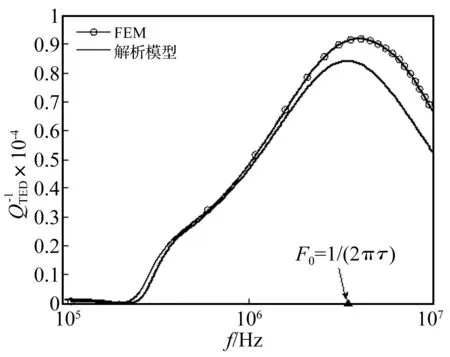
图2 热弹性阻尼解析模型计算结果与FEM数值仿真结果比较

2.2 实验数据比较

实验数据说明[7-10]，弯扭耦合的单平板和双平板谐振器的热弹性阻尼很重要，不能忽略。Liu等[9]测量了单平板MEMS谐振器在不同温度、1-1模态(470 kHz)下的内部耗散(主要为热弹性阻尼)。这个实验是在微平板底部放置压电激励器驱动微平板做弯扭耦合简谐振动，并给出了激光退火后谐振器件的内部耗散与温度的关系。该器件由单晶硅制造，基本尺寸见表1(模型2)，材料特性参数：E=169 GPa，α=2.6×10-6K-1，ρ=2 30 ×10-18kg μm-3，Cp=699×1012pJ (kg·K)-1，χ=0.86×10-4m2s-1，ε=8.854×10-6pF μm-1。

图3给出了该谐振器内部耗散随温度变化的实验数据以及热弹性阻尼解析模型计算结果。为了方便计算，解析模型利用了简化的微平板动态位移比βs，并假设受力位置r=a/2。如图所示，解析模型计算的结果与实验数据接近并具有相同的趋势。在室温下，热弹性阻尼在内部耗散中占重要比例。值得注意的是，在高阶模态下，微平板内部也会产生可观的热弹性阻尼，但是解析模型将微平板看成刚体，从而忽略了这部分由微平板产生的热弹性阻尼。相反，在相对较低的振动频率，微平板内部产生的热弹性阻尼可以忽略。

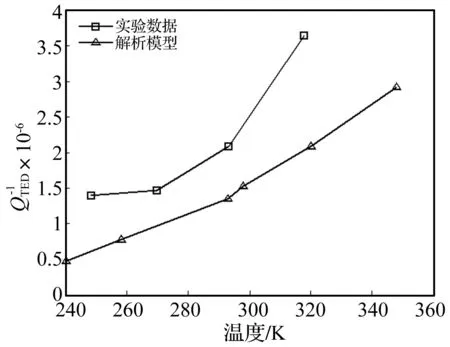
图3 不同温度下热弹性阻尼解析模型计算结果与实验数据比较

3 器件几何尺寸对热弹性阻尼的影响

假设研究的MEMS扭转谐振器件为多晶硅制造，真空封装，并且忽略其他外部阻尼的影响。器件的材料特性参数与FEM仿真所使用的相同。本文从两个方面研究器件的几何尺寸对热弹性阻尼的影响：① 支承梁长度l不变，梁的厚度宽度之比b/c对热弹性阻尼的影响；② 支承梁厚度b不变，梁的长宽比l/c对热弹性阻尼的影响。改变几何尺寸时，我们保持扭转刚度不变Kφ，尽量不影响该器件的扭转特性；并且微平板的厚度为定值2 μm。

图4给出了支承梁的厚度宽度之比b/c对pf的影响。梁的长度l=50 μm，偏置电压V0=20 V，其他结构参数见表1(模型1)。如图所示，在低频段，pf随b/c的增大而减小；在高频段，pf随b/c的增大而增大。pf最小值(≈0)和最大值(≈1)分别出现在扭转共振频率ftorsion和弯曲共振频率fbending。表2给出了550 kHz(>fbending)时，不同的b/c对热弹性阻尼的影响。从表中可见，热弹性阻尼随b/c的增大而增大，解析模型与FEM仿真结果相差很小。

图5给出了支承梁的长宽比l/c对pf的影响。梁的厚度b=2 μm，偏置电压V0=20 V，其他结构参数见表1(模型1)。如图所示，在低频段，pf随l/c的增大而增大；在高频段，pf随l/c的增大而减小。pf最小值和最大值分别对应扭转共振频率ftorsion和弯曲共振频率fbending。表3给出了550 kHz(>fbending)时，不同的l/c对热弹性阻尼的影响。从表中可见，热弹性阻尼随l/c的增大而减小；解析模型与FEM仿真结果很接近。

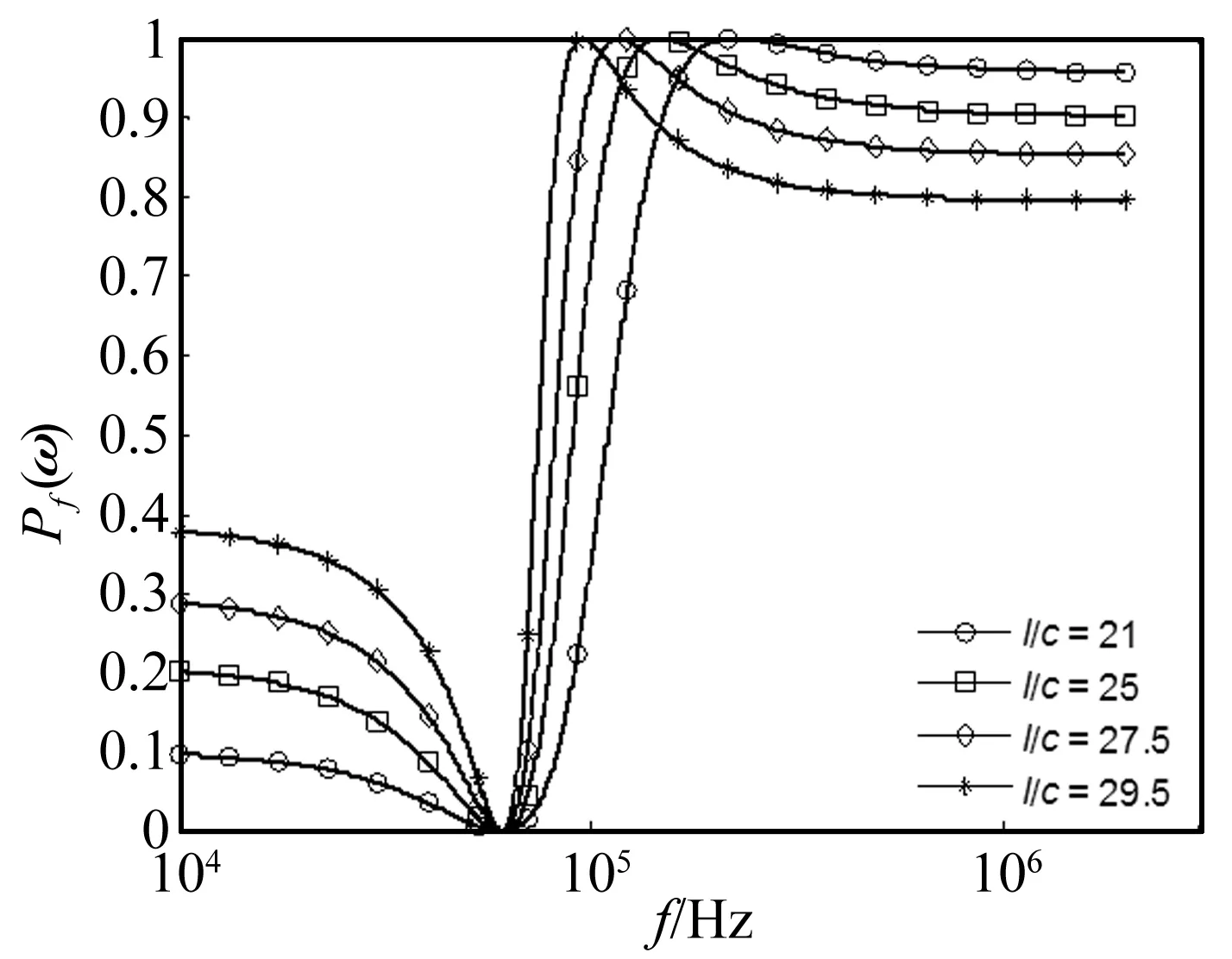
图5 支承梁不同几何尺寸l/c对应的能量比pf曲线

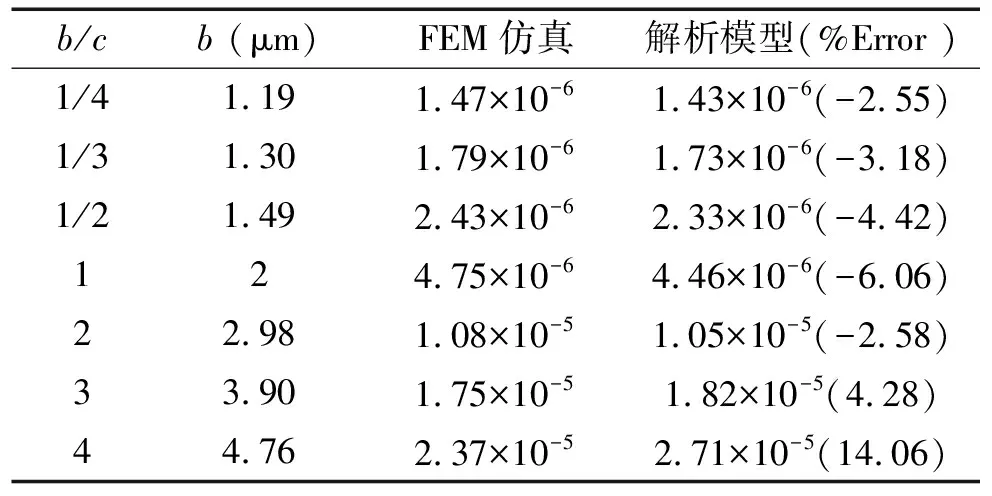
表2 不同b/c对应的热弹性阻尼

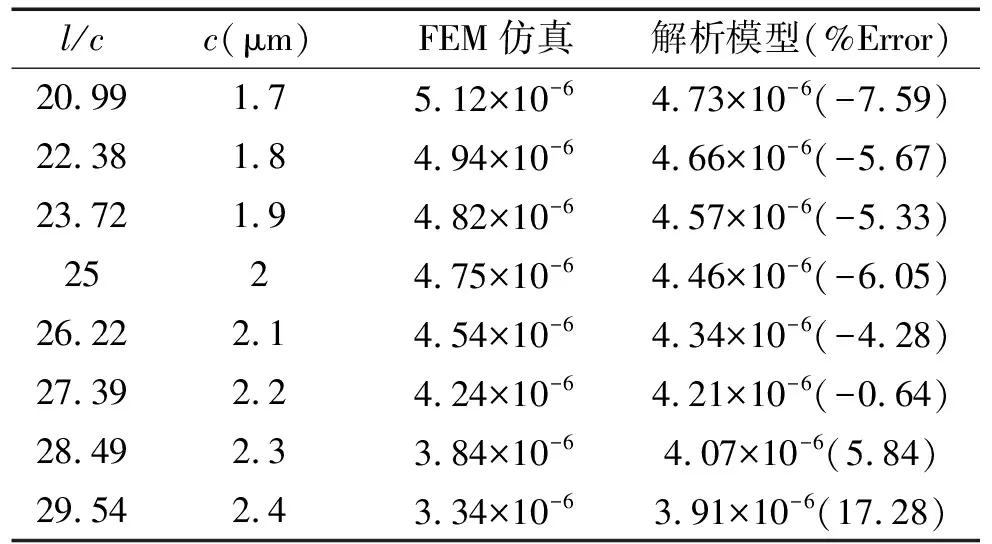
表3 不同l/c对应的热弹性阻尼

4 结 论

本文首先研究了弯扭耦合MEMS谐振器件的静态平衡方程和动力学方程，以此为基础，在假设微平板为刚体的前提下，推导出热弹性阻尼的解析模型。从而解决了Zener和LR等经典理论不能计算弯扭耦合MEMS扭转谐振器件的热弹性阻尼的问题。通过对解析模型特性的研究，本文发现热弹性阻尼受器件几何尺寸影响较大，尤其是器件厚度的影响最明显。本文推导的解析模型与FEM数值仿真结果作比较，结果说明解析模型与数值仿真拟合度很高，误差很小。通过与实验数据比较，说明热弹性阻尼在弯扭耦合MEMS扭转器件的内部耗散中占重要比例。该解析模型在热弹性阻尼的计算中效率更高，对于同类器件的设计和优化具有很高的参考价值。

[1] 李普, 方玉明. 考虑直流偏置电压影响的弹性悬臂微梁挤压膜阻尼新模型[J]. 振动工程学报, 2009, 22(2): 123-127.

LI Pu, FANG Yu-ming. A squeeze-film damping model for flexible cantilever microbeam under the effect of DC bias voltage[J]. Journal of Vibration Engineering, 2009, 22(2): 123-127.

[2] Zener C. Internal friction in solids. Ⅰ. Theory of internal friction in reeds [J]. Physical Review, 1937, 52(3):230-235.

[3] Zener C. Internal friction in solids Ⅱ. General theory of thermoelastic internal friction [J]. Physical Review, 1938, 53(1): 90-99.

[4] Lifshitz R, Roukes M L. Thermoelastic damping in micro-and nanomechanical systems [J]. Physical Review B, 2000, 61(8): 5600-5609.

[5] Prabhakar S, Vengallatore S. Theory of thermoelastic damping in micromechanical resonators with two-dimensional heat conduction [J]. Journal of Microelectromechanical Systems, 2008, 17(2): 494-502.

[6] Chandorkar S A, Candler R N, Duwel A, et al. Multimode thermoelastic dissipation [J]. Journal of Applied Physics, 2009,105(4): 043505-1-12.

[7] Liu X, Morse S F, Vignola J F, et al. On the modes and loss mechanisms of a high Q mechanical oscillator [J]. Applied Physics Letters, 2001 78: 1346-1348.

[8] Houston B H, Photiadis D M, Vignola J F, et al. Loss due to transverse thermoelastic currents in microscale resonators [J]. Materials Science and Engineering a-Structural Materials Properties Microstructure and Processing, 2004, 370: 407-411.

[9] Liu X, Haucke H, Vignola J F, et al. Understanding the internal friction of a silicon micro-mechanical oscillator [J]. Materials Science and Engineering a-Structural Materials Properties Microstructure and Processing, 2009, 521(22): 389-392.

[10] Houston B H, Photiadis D M, Marcus M H, et al. Thermoelastic loss in microscale oscillators [J]. Applied Physics Letters, 2002, 80: 1300-1302.

[11] Huang J M, Liu A Q, Deng Z L, et al. An approach to the coupling effect between torsion and bending for electrostatic torsional micromirrors [J]. Sensors and Actuators A, 2004, 115(1): 159-167.

[12] Zhao J P, Chen H L, Huang H M, et al. A study of dynamic characteristics and simulation of MEMS torsional micromirrors [J]. Sensors and Actuators A, 2005, 120(1): 199-210.

[13] Li P, Hu R F. Thermoelastic damping in micromechanical resonators with a proof mass and a network of suspension beams [J]. Japanese Journal of Applied Physics, 2011, 50(7): 077202(1-10).