大跨度双幅连续钢箱梁桥涡激振动特性风洞试验研究

秦 浩，廖海黎，李明水

(西南交通大学 风工程试验中心 成都 610031)

大跨度钢箱梁连续梁桥由于阻尼小，在常遇风速下存在发生涡激振动可能。自塔科马大桥(Tacoma Bridge)发生风毁以来[1]，大跨度桥梁包括悬索桥、斜拉桥等抗风问题为桥梁工程界所关注。连续梁桥由于跨度小，刚度大等特点，通常认为其抗风性能较好，对其抗风研究较少。随桥梁建设发展，连续梁桥跨度越来越大，在常遇风速(5～20 m/s)下发生涡激振动桥梁屡有报道[2-4]，尤其2010年俄罗斯伏尔加河连续梁桥在低风速下发生的“波浪式起伏”涡激振动，振幅高达40～70 cm，足已影响大桥的使用性能。涡激振动已成为大跨度钢箱梁连续梁桥抗风设计的重要问题。

涡激振动理论研究至今仍无成功的解析方法能从基本流动原理出发描述弹性钝体在周期脱落的漩涡作用下响应全过程，解析复杂外形钝体的涡激响应更难实现。随计算机技术进步，数值方法取得较大进展，但通过数值计算直接模拟三维流场仍受限制，较难处理高雷诺数下三维复杂外形钝体的涡激振动问题。对大跨度连续梁桥变截面复杂外形的钝体结构，研究其涡激振动主要手段为通过全桥气弹模型风洞试验[5]。对常规尺度的全桥模型，比例尺为1:100以上，模型尺寸较小风速比大对主梁细节模拟不够精细，可能导致试验结果(振幅及发生风速)与实桥出入较大，或测不到涡激振动，导致误判实桥涡激振动性能[6]。大尺度模型尺寸可将主梁断面细节、检修车轨道等附属设施模拟更精确，使风洞试验结果接近真实情况。大尺度模型受风洞规模及试验段尺寸限制，风洞阻塞度对试验结果影响不可忽视[7]。

1 试验工况与模型

以崇启大跨度连续梁桥为工程背景。主桥设计方案为六跨连续钢箱梁结构，跨径102 m+185 m×4+102 m，总跨长944 m。主梁为变截面钢箱梁、分离式双幅桥面结构，单幅桥宽16.1 m，跨中梁高4.8 m，墩顶处梁高9 m，边墩处梁高3.5 m，主梁高度按二次抛物线变化，主梁截面见图1。大桥所处地段气象复杂多变，灾害性天气频繁，桥位处风大浪急且台风期长，严重威胁大桥施工安全。设计基准风速高达49.4 m/s，桥址处常遇风速超过15 m/s。

图1 主梁横截面图

试验在XNJD-3风洞中进行，据该风洞试验段尺寸H=4.5 m，W=22.5 m，L=36 m，气弹性模型几何缩尺比取1:45(风洞阻塞率小于1.5%)，为目前连续梁桥最大比例尺全桥气弹风洞试验模型。

由于连续梁桥受力特点，大跨度连续主梁结构采用变截面带悬臂设计。主梁截面高度沿跨度变化使每个断面的斯特罗哈尔数(Strouhal Number)不同，整个主梁涡激振动为综合效应。该综合斯特罗哈尔数St，涡脱频率f，物体特性尺度D(采用跨中梁高)及来流风速U关系为St=fD/U。

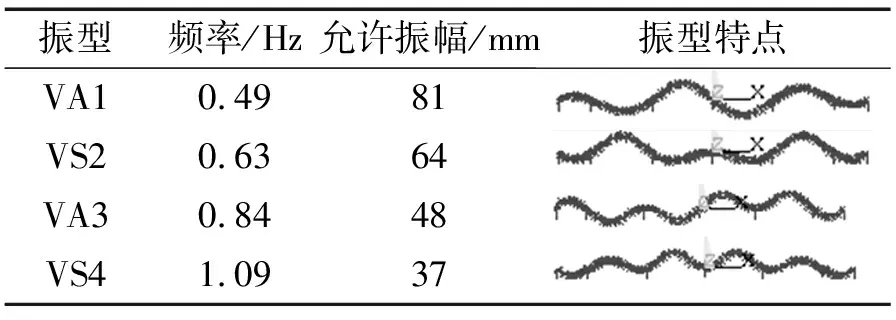
表1 振动模态

模型设计制作采用传统气动弹性模型技术，即芯梁提供结构刚度，芯梁外覆节段以模拟气动外形，质量由外覆结构中配重物提供。主梁共分81节段，除中间5个墩顶处节段外，每个节段长160 mm，中间4跨每跨按梁段高度变化分15节段，最长节段311 mm，最短节段186 mm，边跨分8节段，最长节段302 mm，最短节段186 mm，气弹模型照片见图2。试验通过在中间四跨跨中安置激光位移传感器测量竖向振动，采样频率256 Hz，单次采样时间32 s。

图2 气弹性模型照片

风洞试验之前，用强迫振动法对气弹模型进行模态测试检验，结果见表2。由表2看出，该模型频率误差在2%以内。试验在均匀流中进行，分别为0°攻角及对钢箱梁涡激振动最不利的+3°攻角(由导流板产生)，并通过在第三、四跨中安装油质阻尼器施加结构阻尼，模拟阻尼对涡激振动的减振作用。

试验共6种工况，前3工况在0°攻角下进行，工况1阻尼比水平在0.3%量级，与多数大跨度钢箱梁连续梁桥实测阻尼比接近。工况2阻尼比为0.5%量级，与多数中等跨度连续梁桥实测阻尼比值接近。两种阻尼比分别对应欧洲规范、我国规范对钢梁桥阻尼比的风洞试验设置要求。工况3目的为研究完全抑制涡激响应所需阻尼比水平。后3工况为阻尼比状态风攻角由0°改为+3°时的试验情况。

表2 各工况模态测试结果

2 试验结果及讨论

工况1结果见图3，对0°攻角、一阶竖弯振动阻尼比0.3%量级模型状态，在试验风速范围内存在两明显涡振区：第一涡振锁定风速范围对应于实桥风速15～27 m/s，上风侧主梁竖向锁定风速略小于下风侧主梁，两主梁涡振最大振幅基本一致，分别为79 mm，93 mm，振型特点为中间两跨振动幅度最大，方向相反，频谱图见图4，振动频率6.97 Hz，证实为主梁反对称一阶振动。第二涡振区锁定风速，两侧主梁基本一致，锁定区为30～35 m/s，下风侧主梁涡激响应远高于上风侧主梁，是上风侧主梁的3倍，最大振幅达144 mm，其振型特点为中间两跨振动幅度最大，方向相反，频谱见图5，对应的振动频率6.81 Hz，亦为主梁反对称一阶振动；图6为工况2，风攻角0°，通过加装油质阻尼器将阻尼比提高到0.5%量级。试验结果表明，主梁涡激响应明显减小。增大阻尼比对第一涡振区抑制效果超过60%，最大振幅29 mm，第二涡振区抑制效果为30%，最大振幅则96 mm。结构阻尼比变化对振型几乎无影响，阻尼变大锁定风速范围变小，相同风速振幅减小，振型应同阻尼比水平0.3%时，限于篇幅不再给出涡激振动频谱图。工况3的试验结果表明，阻尼比为1.1%时，试验中未观测到明显的竖向涡激振动，故结果不再列出。

图3 工况1风速与振幅关系

图5 工况1第2点模型振幅及频谱

图7 工况4风速与振幅关系

工况4的结果见图7，此时风攻角为+3°、阻尼比0.3%量级，主梁涡激响应较0°攻角大。在试验风速范围内，两涡振区几乎合成一个，最大涡激振幅为0°攻角的2倍，振幅299 mm，前一涡振区对应频谱见图8，振动频率6.94 Hz；后一涡振区对应频谱见图9，振动频率为6.88 Hz，振型特点亦中间两跨振动幅度最大，方向相反，为主梁反对称一阶振动。工况5结果见图10，+3°攻角，阻尼比提高到0.5%量级，两涡振区已明显削弱。阻尼比增大到1.2%时(工况6)，试验未观察到明显涡激振动。

0°攻角第一主涡振区St为0.12，与采用单幅主梁六车道的东京湾通道桥(桥宽29.9 m，跨中桥高6 m)实测值及风洞试验值0.12一致[4]。第二主涡振区St为0.07(特征尺度D采用跨中主梁高度)。

双幅主梁涡激振动机理为第一涡振区St与东京湾通道桥一致，其涡激振动机理应为上风侧主梁在均匀流下的涡激振动响应。因分离式双幅主梁特点为两幅主梁结构相同，振动模态完全一致，两幅主梁距离较近，其中单幅主梁振动在周围气流带动下易激起另一主梁的振动。上风侧主梁涡激振动产生的尾流激起下风侧主梁发生共振，其振幅大小与上风侧主梁一致；第二涡振区St较第二涡振区St约大一倍，可理解为两幅主梁较单幅主梁特征宽度尺寸增大一倍，其涡激振动机理为下风侧主梁在均匀流下的涡激振动响应，下风侧主梁的涡激振动反激起上风侧主梁发生共振，表现为下风侧主梁涡激振幅大于上风侧主梁。

图9 工况4第2点振幅及频谱

文献[1,11]通过半经验模型讨论涡激振动时，无量纲振幅y/D与Sc为Sc=4πζm/ρD2，其中ζ为结构阻尼比，m为单位长度等效质量，ρ为空气密度，D为跨中梁高。试验所测0°攻角时最大无量纲振幅y/D与Sc间关系见图11。

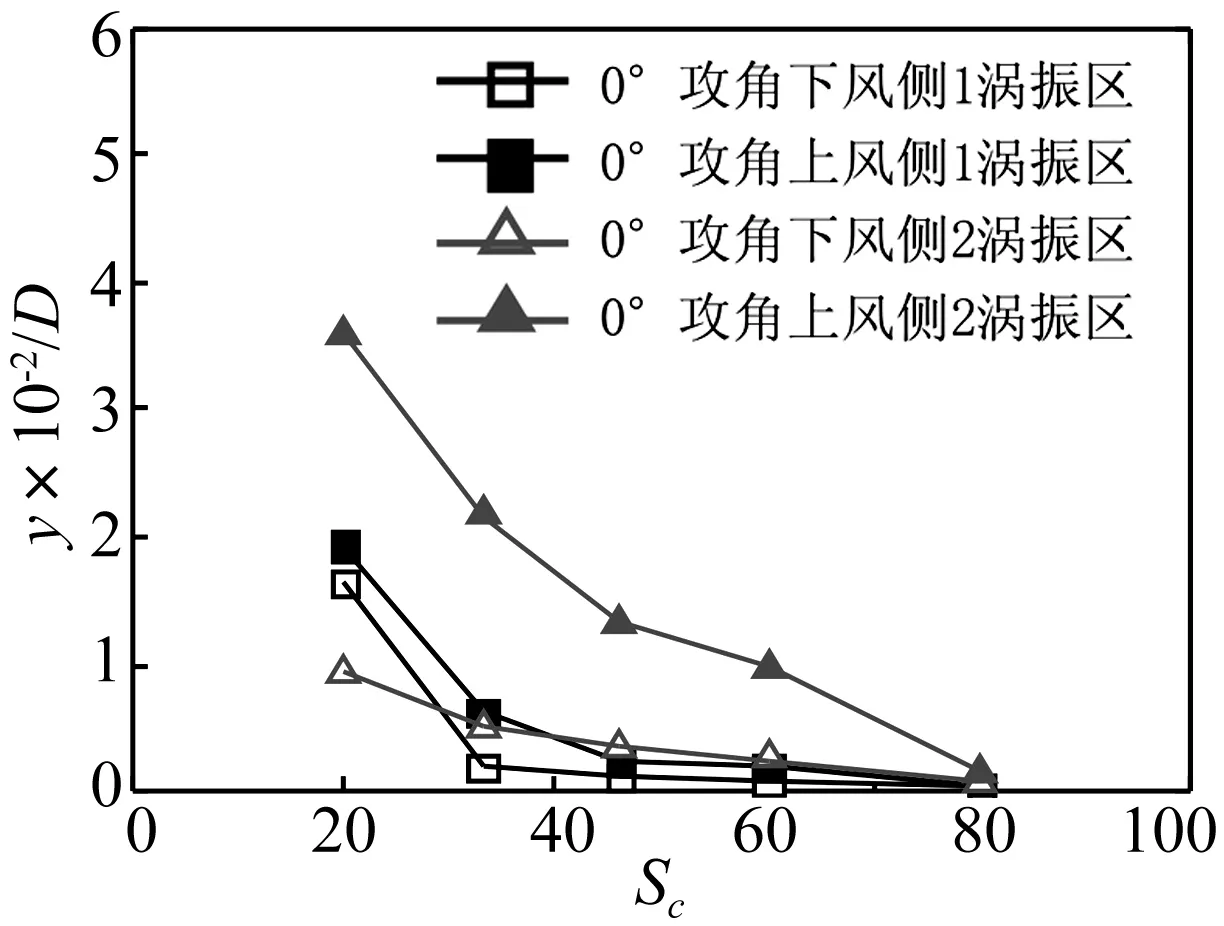
图11 无量纲振幅y/D与Sc关系

3 结 论

通过崇启大桥全桥气弹性模型风洞试验，对连续钢箱梁桥抗涡激振设计，结论如下：

(1) 连续钢箱梁桥主梁涡激响应最大St数约为0.12表明，大跨度连续梁桥一阶竖弯振动频率小于0.7 Hz时，发生涡激振动的风速在30 m/s以下，需结合桥址处风环境考虑是否进行专门抗风设计；而对跨海桥常遇风速较高、风场湍流度较小情况，需进行抗涡激振动研究与设计。

(2) 分离式双幅主梁间易形成共振，涡激响应存在两个涡振区，第一涡振区St数为0.12，第二涡振区为0.07，前一涡振区对应于上风侧主梁涡激响应，下风侧主梁为上风侧主梁涡激响应引起的共振，两侧主梁涡激振幅相当，后一涡振区为下风侧主梁涡激响应，引起上风侧主梁共振，下风侧主梁涡激振幅强于上风侧主梁。

(3) 附加阻尼对涡激振动有较好抑制作用。结构阻尼比达到1.2%时，风速40 m/s范围内不会发生明显涡激振动。

[1] SimiuI E, Scanlan R H.Wind effects on structures:fundamentals and applications to design(3rd edition)[M].New York: John Wiley & Sons, Inc., 1996.

[2] Schewe G, Larsen A.Reynolds number effects in the flow around a bluff bridge deck cross section[J].Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74/76: 829-838.

[3] Fujino Y, Yoshida Y.Wind induced vibration and control of tans-tokyo bay crossing bridge[J].Journal of Structural Engineering, 2002,128(8):1012-1025.

[4] 鲜荣,廖海黎,李明水.大比例主梁节段模型涡激振动风洞试验分析[J].实验流体力学, 2009, 23(4):15-20.

XIAN Rong, LIAO Hai-li, LI Ming-shui.Analysis of vortex-induced vibration of large scale section model of girder in wind tunnel[J].Journal of Experiments in Fluid Mechanics, 2009, 23(4):15-20.

[5] Ehsan F, Scanlan R H.Vortex-induced vibrations of flexible bridges[J].Journal of Engineering Mechanics, 1990,116(6): 1392-1410.

[6] 项海帆.现代桥梁抗风理论与实践[M].北京:人民交通出版社, 2005.

[7] 张伟,魏志刚,杨詠昕,等.基于高低雷诺数试验的分离双箱涡振性能对比[J].同济大学学报(自然科学版), 2008, 36(1): 7-11.

ZHANG Wei, WEI Zhi-gang, YANG Yong-xin.Comparison and analysis of vortex induced vibration for twin-box bridge sections based on experiments in different Reynolds number[J].Journal of Tongji University(Natural Science), 2008, 36(1): 7-11.

[8] 陈政清.桥梁风工程[M].北京: 人民交通出版社, 2005.

[9] 陈艾荣.崇启大桥抗风研究[R].上海: 同济大学, 2009.

[10] JTG/YD60-01-2004,公路桥梁抗风设计规范[S].

[11] 鲜荣,廖海黎,李明水.大跨主梁沿跨向涡振Scanlan非线性模型应用[J].振动与冲击,2009,28(4):54-58.

XIAN Rong, LIAO Hai-li, LI Ming-shui.The application of Scanlan’s nolinear model to describe spanwise votex-induced vibration of long-span bridge girder[J].Journal of Vibration and Shock,2009, 28(4):54-58.

[12] 许福友,丁威, 姜峰,等.大跨度桥梁涡激振动研究进展与展望[J].振动与冲击, 2010,29(10):40-49.

XU Fu-you, DING Wei, JIANG Feng,et al.Development and prospect of study on vortex-induced vibration of long-span bridges[J].Journal of Vibration and Shock, 2010,29(10):40-49.