蜂窝状空腔屏障隔振效果分析

徐 平

(郑州大学 交通运输工程系，郑州 450001)

动力机器、铁路、公路、爆炸、打桩、强夯等引起的振动公害日益频繁，对临近建筑物及地下管线、精密仪器、设备、生活工作环境造成不容忽视影响。国际上已将人工振动列为七大公害之一，各种人工振动对环境影响及治理研究已成土动力学领域热点[1]。屏障为缓解建筑施工、铁路与公路交通、工业、爆破等所致振动强度的主要措施[2]。

目前，关于开口沟渠与混凝土墙等形式的连续屏障理论及试验研究已较成熟。Ahmad等[3]对空沟、填充沟等隔振效果研究结果表明，隔振沟效果主要取决于沟深与表面波波长之比，沟深小于表面波波长30%时，空沟对低频振动几乎无隔振效果；谢伟平等[4]对武汉轻轨产生振动的隔振措施研究表明，地下连续墙能有效减少轻轨运行产生的地面振动，但对波长较大的低频振动，连续墙深度足够深时才有效。对非连续屏障，徐平等[5-8]分别对多排柱腔、多排桩等构成的非连续屏障对弹性波隔离效果分析结果表明，随柱腔或桩排数的增多，隔离效果明显提高，综合经济及隔离效果，三排柱腔或桩构成的屏障最合适。Schmid等[9]提出在土中建造“人工基岩”屏蔽土层振动，“人工基岩”称为波阻块(WIB)。因土中存在刚性基底，土体有某些内在固有模态，并具有一定截止频率范围，任何超出土层截止频率范围的振动模态均不能产生。

本文将蜂窝状空腔屏障[10]用于厂房周边或交通干道旁隔振。蜂窝状空腔屏障介于空沟与多排柱腔间的隔振措施，蜂窝壁可用木板或混凝土浇注，空腔内可填充泡沫、废弃橡胶轮胎等，整个屏障上部搭板可种植花草，经济、环保、高效。本文在文献[5-8]基础上，用复变函数的保角映射方法与波函数展开法，获得蜂窝状空腔屏障理论解，并分析其对平面SV波隔离效果。

1 蜂窝状空腔屏障映射变换

带正多边形孔的无限平面均可通过保角映射到单位圆内部，变换公式[11]为

(1)

式中：n为正多边形边数；ζ=aeiθ为映射后半径a的圆；c=Reiδ，R为实常数，δ为孔对基本位置所转角度。

蜂窝状空腔屏障有若干正六边形空腔组成，即n=6，进行映射变换时不计角度转变，即δ=0°，则式(1)可化简为

ω(ζ)=

(2)

将式(2)中ζ与1/ζ互换，则式(2)即为带正六边形孔的无限平面保角映射到单位圆外部变换公式：

ω(ζ)=

(3)

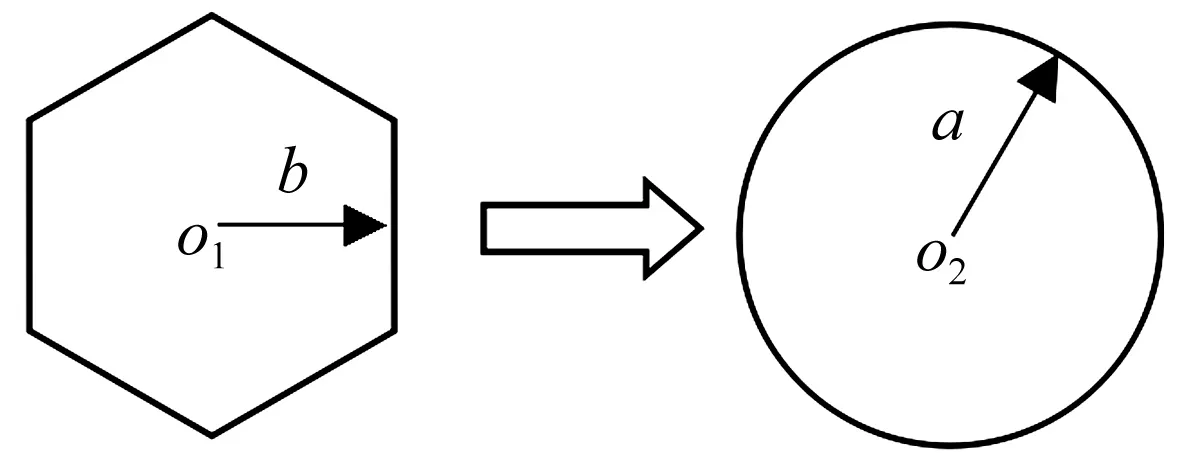
图1 正六边形映射到圆

取单个蜂窝状空腔正六边形边长b，映射后圆半径a，见图1。据图1、式(3)可将蜂窝状空腔屏障映射成复平面上多排圆形孔结构，见图2。

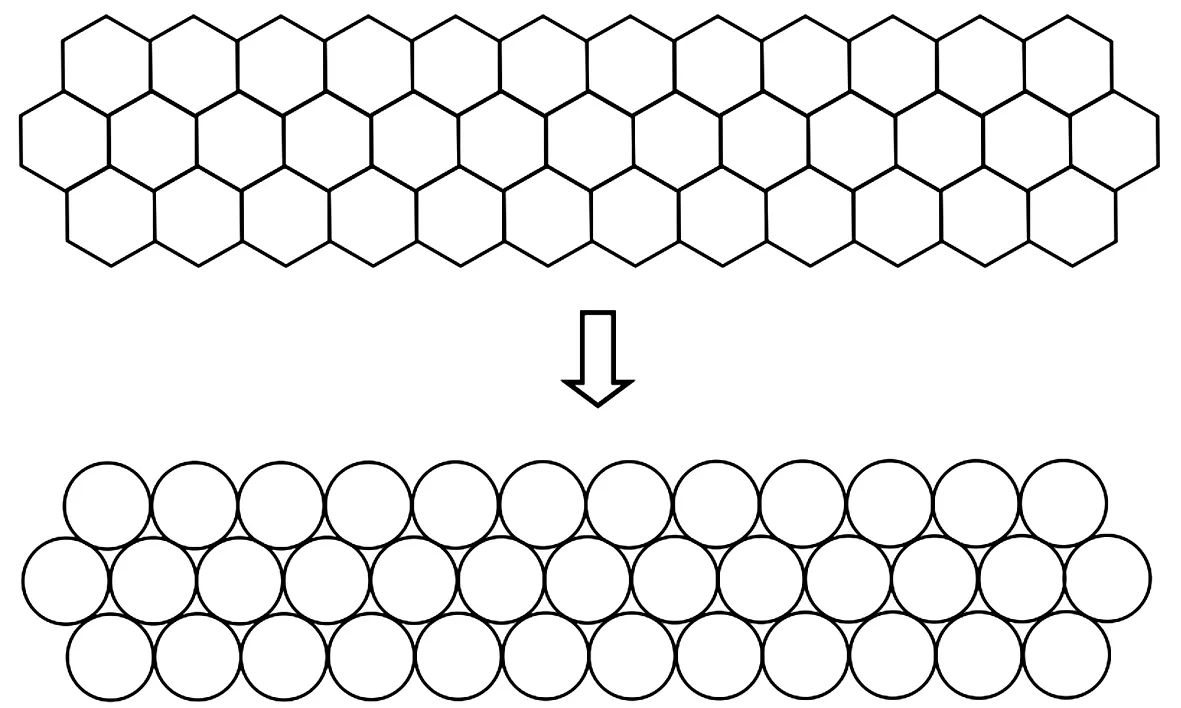
图2 蜂窝状空腔屏障映射到多排圆形孔

2 波场位移势函数表达式

2.1 入射SV波位移势函数

将周围土体视为各向同性的无限均质弹性体，考虑蜂窝状空腔屏障单体深度远大于直径，可将蜂窝状空腔屏障对平面SV波隔离问题简化为二维平面问题。设WIB结构由N个单体组成，映射后N个圆孔，引入N个局部坐标系(xj,yj)(1≤j≤N),见图3。

图3 映射后圆孔分布及坐标系设置

入射频率为ω的SV波位移势函数可写成：

winc=w0eiks(xcosβ+ysinβ)

(4)

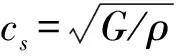
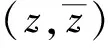
(5)

(6)

2.2 散射SV波势函数

(7)

(8)

(9)

(10)

3 散射系数求解

复坐标系下SV波位移引起的剪应力算式为

(11)

设蜂窝状空腔屏障界面完全自由(应力为零)：

(12)

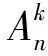
(13)

(14)

(15)

(16)

4 数值计算

为简化计算，设蜂窝状空腔屏障单体尺寸均相等，通过保角变换的柱腔半径均为a。对SV波引起的位移场频率归一化处理：

(17)

式中：η为归一化后土体中位移场频率；λs为土体中SV波波长。

4.1 本文公式及计算程序正确性验证

取ω(ζ)=ζ，则式(14)即可简化为多圆形柱腔列屏障对SV波散射系数的解答。取无量纲入射频率η=0.4，以单排柱腔列(间距d/a=3.0、个数N=8)为例，获得屏障后中心线上归一化位移幅值 (即屏障后竖向位移与入射平面SV波竖向位移幅值比值)变化曲线，并与直角坐标系下解答[13]对比，见图4。由图4看出，本文用复变函数积分变换法所得解答与用Graf加法法则所得解答[12]完全吻合，本文公式与计算程序的正确性得以验证。

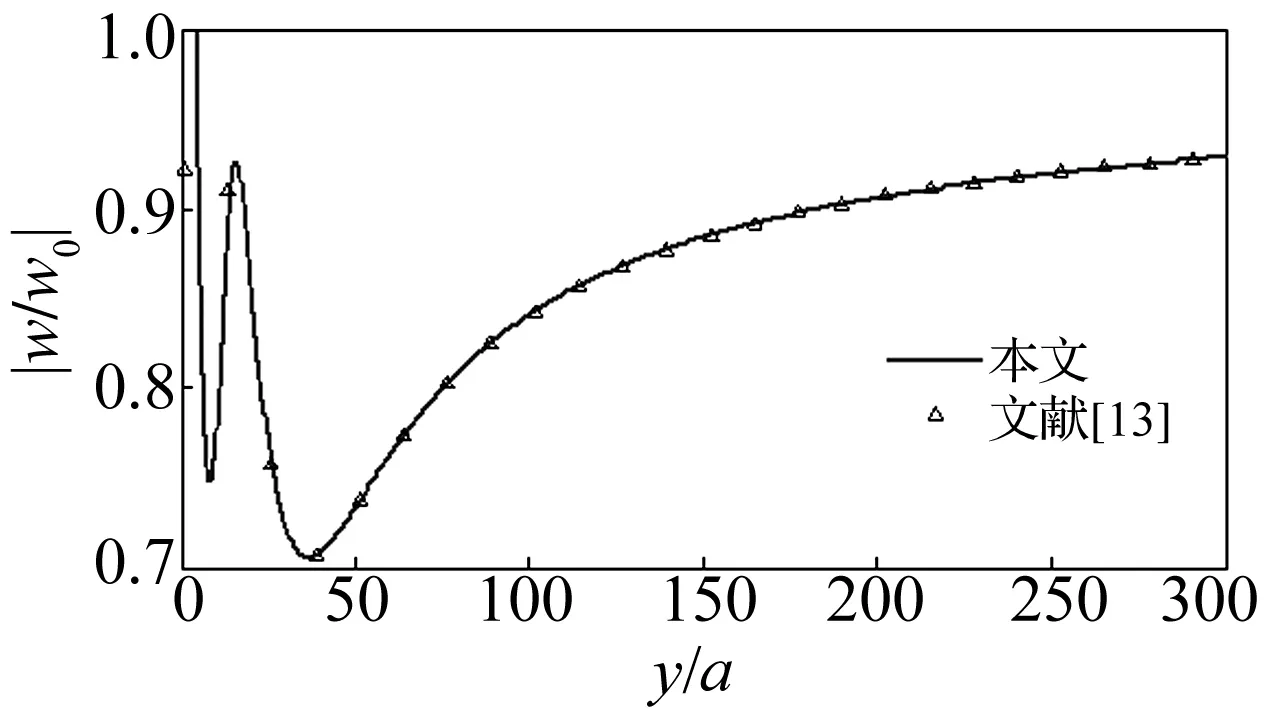
图4 屏障中心线上变化曲线

据式(3)获得由单位圆映射为正六边形图形见图5。由图5看出，式(3)的映射函数接近正六边形，可用于蜂窝状空腔屏障对SV波隔离问题计算。

图5 由单位圆映射所得正六边形

取蜂窝状空腔屏障坐标体系见图6，圆心取第一排左起第一个空腔中心，x轴平行屏障方向，y轴平行屏障方向。

图6 蜂窝状空腔屏障排列

(1) 所有蜂窝状空腔屏障(二排或三排，整体宽度L/a=8或12)对高频SV波隔离效果好于低频SV波，即频率越高，入射SV波在屏障壁上散射、反射能量越大，穿过屏障散射到屏障后的SV波能量越低，隔振效果越好；

(2) 无论二排或三排屏障，靠近屏障边缘区域隔离效果好于中心区域，此因屏障中心SV波能量叠加高于两侧；

(3) 屏障整体宽度较短时(L/a=8)，随排数的增大(由二排提高三排)，隔离效果提高不明显，但当整体宽度较长时(L/a=12)，随排数的增大(由二排提高三排)，隔离效果明显提高；

(5) 进行隔振工程设计，综合隔离效果、施工、维护费用等因素，三排蜂窝状空腔屏障最优，以本文算例图9为例，在屏障后的研究区域内，对较低频率SV波，大约1/4面积隔离效果均超50%，而对较高频率SV波，整个研究区内隔离效果均超70%，近3/4面积隔离效果超过80%，隔离效果非常理想。

图7 二排(8+9) 蜂窝状空腔屏障后|w/w0|等值线

图10 三排(12+13+12) 蜂窝状空腔屏障后等值线

4.2 三种屏障隔振效果对比

取三排蜂窝状空腔屏障(12+13+12)、三排柱腔屏障(8+9+8)，整体宽度L/a=24，分别用本文与文献[5]方法计算。空沟屏障宽1.0 m、长12.0 m、深10.0 m，用Abaqus有限元计算。无量纲入射频率η=0.4，获得屏障中心线上 变化曲线，见图11。由图11看出，基于波动理论计算的多排蜂窝状空腔屏障、多排柱腔屏障，在靠近屏障区域位移幅值会局部放大，主要由波的散射、来回反射造成，而空沟主要为波的绕射，因此位移幅值不会增大。最佳隔振效果为空沟(89.7%)>三排蜂窝状空腔屏障(85.4%)>三排柱腔列(76.2%)，远处隔振效果为空沟(50.1%)>三排蜂窝状空腔屏障(42.2%)>三排柱腔列(18.9%)，表明三排蜂窝状空腔屏障隔振效果介于空沟与三排排柱腔屏障之间，接近于空沟。

5 结 论

(1) 基于波动函数理论，运用正六边形与圆孔保角变换法，获得蜂窝状空腔屏障对SV波隔离理论解；

(2) 屏障对较高频率SV波隔离效果好于较低频率SV波；靠近屏障边缘区域隔离效果好于中心区域；屏障对SV波隔离效果随屏障整体宽度增长、排数增多明显提高；综合隔离效果、施工、维护费用等因素，三排蜂窝状空腔屏障最优，在屏障后区域内，较低频率SV波有约1/4面积隔离效果超过50%；而较高频率SV波在整个区内隔离效果均超过70%，近3/4面积隔离效果超过80%，隔离效果非常理想。

(3) 通过对比获得三种屏障隔振效果大小关系，即三排蜂窝状空腔屏障介于空沟与三排多排柱腔屏障之间，接近于空沟。

[1] 孙雨明, 李伟, 高广运.Gibson地基波阻板隔振分析[J].西北地震学报, 2011, 33(1): 40-46.

SUN Yu-ming, LI Wei, GAO Guang-yun.Analysis of vibration isolation using WIB for Gibson ground[J].Northwestern Seismological Journal, 2011, 33(1): 40-46.

[2] Woods R D.Screening of surface waves in soils[J].Journal Solids Mech.and Found.Div.ASCE., 1968, 94(4): 951-979.

[3] Ahmad S, Al-hussaini T M, Fishman K L.Investigation on active isolation of machine foundations by open trenches [J].Journal Geotech.Engng., 1996, 122: 454-461.

[4] 谢伟平, 常亮, 杜勇.中南剧场隔振措施分析[J].岩土工程学报, 2007, 29(11) : 1720-1725.

XIE Wei-ping, CHANG Liang, DU Yong.Analysis on vibration isolation of Zhongnan Theater[J].Chinese Journal of Geotechnical Engineering, 2007, 29(11): 1720-1725.

[5] 徐平.多排柱腔构成的非连续屏障对SV波的隔离[J].振动与冲击, 2009, 28(12): 84-87.

XU Ping.Isolation of plane SV waves by discontinuous barriers composed of several rows of cylindrical cavities[J].Journal of Vibration and Shock, 2009, 28(12): 84-87.

[6] 徐平.多排柱腔列对P波和SH波的隔离[J].工程力学, 2011, 28(5): 78-83.

XU Ping.Isolations of plane P and SH waves by barriers composed of several rows of cylindrical cavities[J].Engineering Mechanics, 2011, 28(5): 78-83.

[7] 徐平.多排空心管桩屏障对平面SV波的隔离[J].岩土工程学报, 2011, 33(3): 392-397.

XU Ping.Rows of elastic hollow pipe piles as isolation barriers for plane SV waves[J].Chinese Journal of Geotechnical Engineering, 2011, 33(3): 392-397.

[8] 徐平.多排桩非连续屏障对平面弹性波的隔离[J].岩石力学与工程学报, 2012, 31(S1): 3159-3166.

XU Ping.Isolation of plane elastic waves by discontinuous barriers composed of several rows of piles[J].Chinese Journal of Rock Mechanics and Engineering, 2012, 31(S1): 3159-3166.

[9] Schmid G, Chouw N, Le R.Shielding of structures from soil vibrations[C].// Proceedings of Soil Dynamics and Earthquake Engineering V, Computational Mechanics Publications, 1992: 651-662.

[10] Takemiya H.Hybrid procedure of field measurement and computer simulation to develop WIB for vibration mitigation from traffic viaduct[C].//Proceedings of Environmental Vibrations Prediction, Monitoring, Mitigation and Evaluation, Volume I, Beijing: Science Press, 2009: 223-230.

[11] 萨文 P H,著.卢鼎霍,译.孔附近的应力集中[M].北京: 科学出版社, 1958: 6-16.

[12] Liu Dian-kui.Applications of the method of complex function to dynamic stress concentration[J].Wave Motion, 1982,4(3): 293- 304.

[13] Avilés J, Sánchez-sesma F.Piles as barriers for elastic waves[J].Journal Geotech.Engng., 1983,119(9):1133-1146.